Algorithm - Backtracking - N-Queens

트리의 방문 순서

preorder

• 자신 > 왼쪽 자식 > 오른쪽 자식 순으로 방문한다.
  

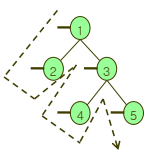
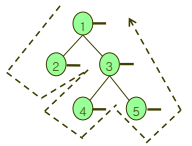
inorder

• 왼쪽 자식 > 자신 > 오른쪽 자식 순으로 방문한다.

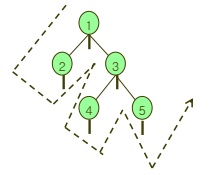
postorder

• 왼쪽 자식 > 오른쪽 자식 > 자신 순으로 방문한다.
  

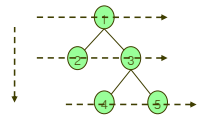
level order

• height순으로 순차적으로 방문한다.
  

depth-first search

• 루트 노드를 먼저 방문한뒤 그 마디의 모든 후손 마디들을 차례로 방문한다.

pseudo code

python

def depth_first_search(graph, startVertex, endVertex):
    stack = StackType()
    vertexQ = QueType()
    found = False
    print(startVertex)
    graph.get_to_vertices(startVertex, vertexQ)
    while not vertexQ.is_empty() and not found:
        item = vertexQ.dequeue()
        if item == endVertex:
            print(item)
            found = True
            return found
        else:
            stack.push(item)
    while not stack.is_empty():
        item = stack.top()
        print(item)
        stack.pop()
        graph.get_to_vertices(item, vertexQ)
        while not vertexQ.is_empty() and not found:
            item = vertexQ.dequeue()
            if item == endVertex:
                print(item)
                found = True
                return found
            else:
                stack.push(item)
    return found

되추적 알고리즘

• 가능한 상태들로 구성된 상태공간트리에서 깊이우선검색을 실시하여 유망성 점검을 한다.

마디의 유망성

• 전형 해답이 나올 가능성이 없는 마디는 유망하지 않다고 표현한다.

되추적 기법

• 각 마디의 유망성을 점검한 후 유망하지 않다고 판단되면 부모 마디로 돌아가 다음 후손 마디에 대한 검색을 진행한다.
• 부모 마디로 돌아가는 것을 pruning이라고 한다.
• 이 과정에서 방문한 마디만으로 구성된 부분 트리를 가지친 상태공간 트리(pruned state space tree)라고 한다.

pseudo code

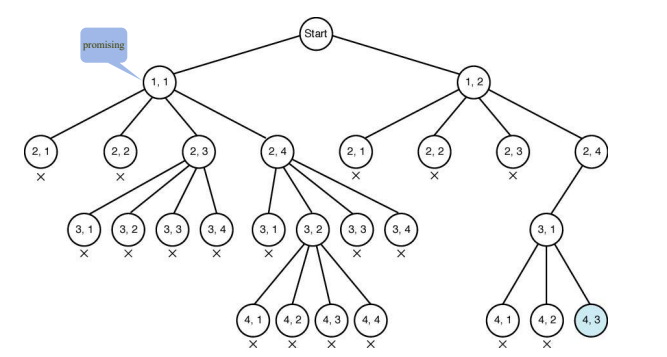
n-queens 문제

• chess판에서 각각의 퀸이 서로 같은 행, 같은 열에 존재하지 않으며 대각선 상에 존재하지 않도록 퀸을 배치하는 문제

되추적 기법의 적용

• 퀸을 배치하는 경우의 수를 나타낸 트리의 마디 유망성을 점검한 후 유망하지 않다고 판단되면 부모 마디로 돌아가 다음 후손 마디에 대한 검색을 진행한다.
  

pseudo code

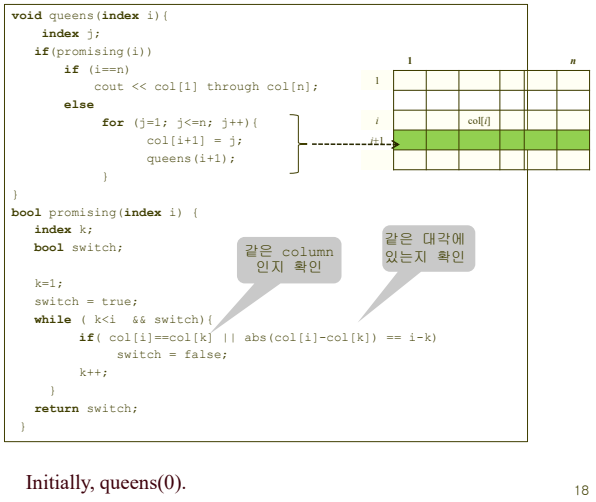
python

• 참고 : 백준 9663번 - n-queens 문제

def promising(i, col):
    global node  # 재귀적으로 호출될 때마다 새로 할당되는 것을 막기 위해 전역변수로 선언합니다.
    node += 1  # 유망한지에 대한 여부를 검사할 때 마다 node의 개수가 늘어납니다.
    k = 0
    switch = True
    # i번째 여왕이 위치와 같은 열 혹은 대각선에 다른 여왕이 위치하면 false를 반환합니다.
    while k < i and switch:
        if col[i] == col[k] or abs(col[i] - col[k]) == i-k:
            switch = False
        k += 1
    return switch

def queens(n, i, col):
    global ans  # 재귀적으로 호출될 때마다 새로 할당되는 것을 막기 위해 전역변수로 선언합니다.
    if promising(i, col):
        if i == n - 1:
            ans += 1
        else:
            for j in range(n):
                col[i+1] = j
                queens(n, i+1, col)
    return ans, node