상호배타적 집합의 처리
- 두 요소가 동일 집합에 속하는 가에 대한 여부를 처리한다.
사용 방법
- linked list 사용방법
- array 사용방법
- tree(forest) 사용 방법
- 단순 방법
- 무게 고려 방법
- path compression 방법
operations
- make_set(v) : make a set with an element v
- find(v): returns a name of the set containing v
- union(u,v): 원소 u와 원소 v를 갖고 있는 집합을 하나로 합친다.
linked list 사용 방법
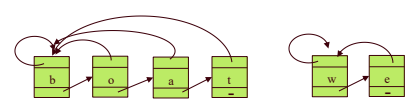
- set의 이름은 최초 원소값으로 설정한다.
- 각 원소는 set이름으로 가는 포인터와 next 포인터를 갖는다.
- make_set(v): O(1) / find(v): O(1)
- union(u,v): u가 속해 있는 리스트의 set이름으로 가는 포인터를 v가 속해있는 set의 이름으로 바꾸어 준다.
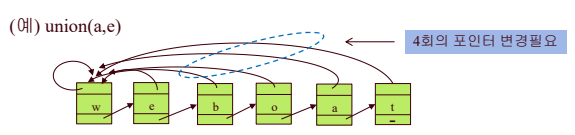
- n개의 데이터에 m번의 union은 O(m^2)소요 (m < n)
개선방법
- 리스트의 크기를 별도로 저장하고 크기가 작은 리스트를 크기가 큰 리스트에 연결한다.
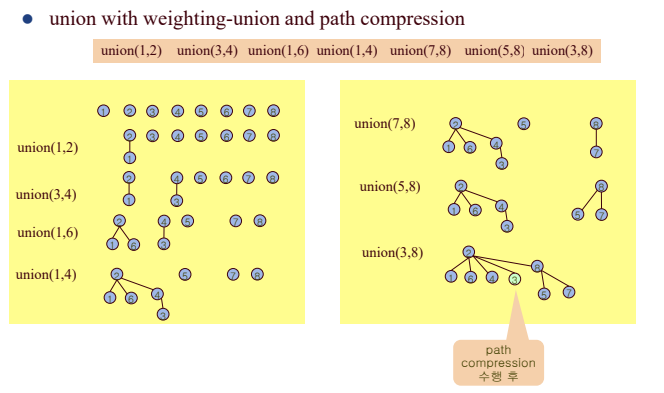
- weighting-union heuristic
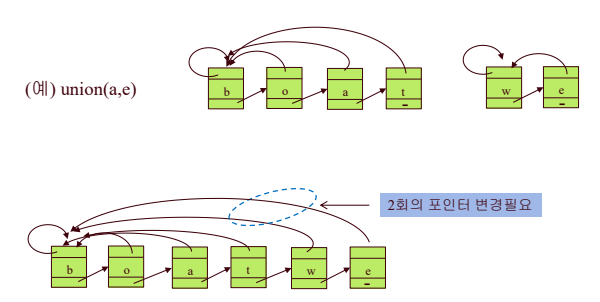
- n개의 원소가 있을 때, 개선된 방법으로 n-1번의 union을 수행하는데O(n lg n) step 소요
array 사용방법
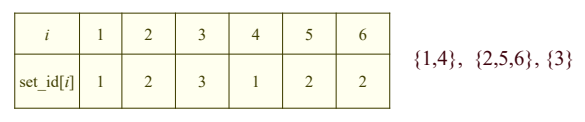
- find(x) : set_id[x]만 확인
- union(x, y): set_id[y]를 갖고 있는 원소들의 set_id로 set_id[x]를 변경
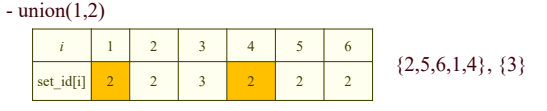
- weighting-union heuristic을 사용하면 시간을 단축할 수 있다.
tree 사용 방법
단순 방법
- 하나의 component는 하나의 트리로 표현한다.
- 전체 그래프가 전체(모든) 집합을 나타낸다.
- root원소가 집합의 이름을 나타낸다.
- 각 원소는 parent로 향하는 포인터를 갖는다.
- find(x): x에서 출발하여 parent로 향하는 포인터를 따라 root로 이동하여, root값을 반환
- union(x,y): find(x) 원소를 find(y)의 child node로 만든다.
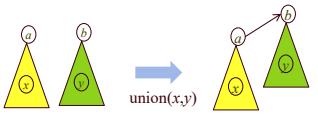
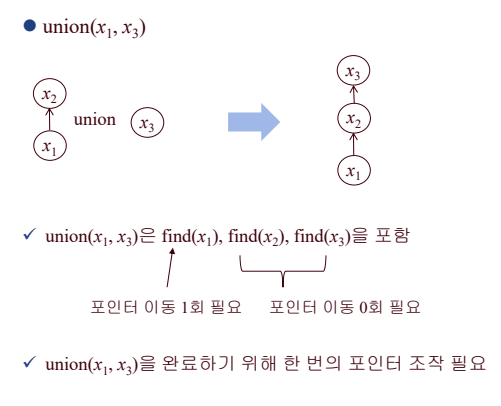
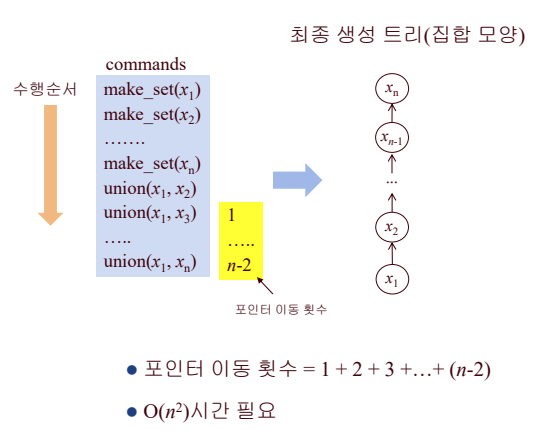
가중치를 고려한 방법
- 트리가 갖고 있는 원소의 weight를 저장한다.
- weight가 작은 것을 weight가 큰 트리에 연결한다.
- 트리의 높이를 이용하여 트리의 rank를 정의한다.
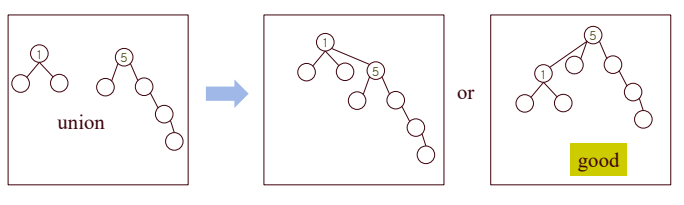
- 결과 트리의 높이가 낮은 것이 유리하다.
- find를 빨리 수행하는 것이 검색하는 것에 있어 바람직하다.
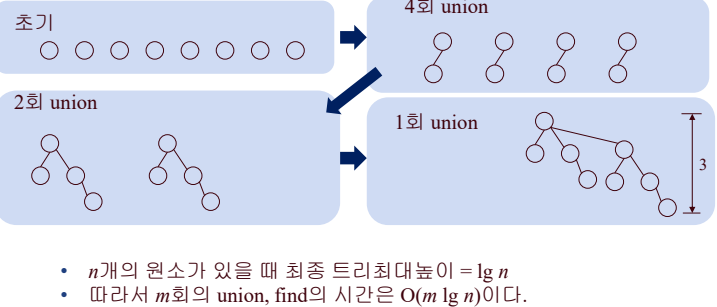
- 이 방법을 사용할 경우 n개의 원소를 갖고 있을 때, forest에 있는 어떠한 트리도 높이가 lg n을 넘을 수 없다.
- O(n) union-find operation은 최대 O(n lg n) 시간 소요
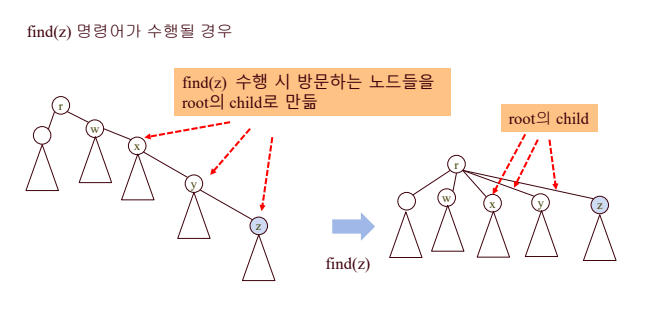
path compression 방법
KHU, SWCON