Algorithm - Greedy algorithm - Dijkstra 알고리즘

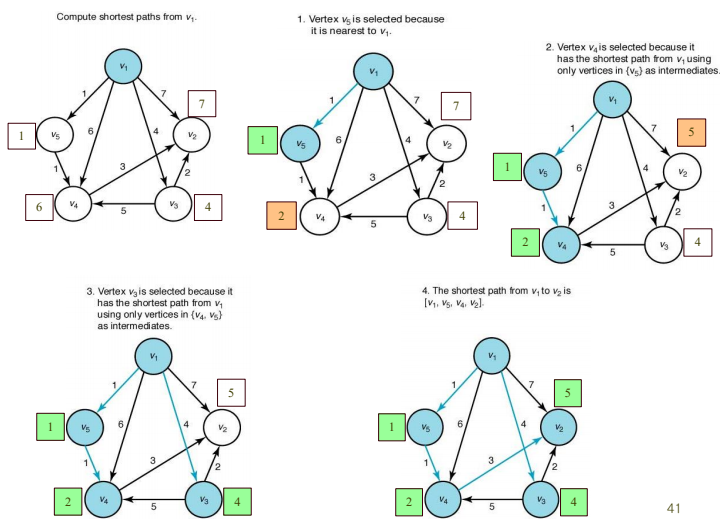
단일출발점 최단 경로 문제

• 가중치가 있는 방향 그래프에서 한 특정 정점에서 다른 모든 정점으로 가는 최단 경로를 구하는 문제

설계절차

• 해답 이음선의 집합인 F를 공집합으로 둔다.

• 해답 정점의 집합인 Y에 출발점인 v1만을 둔다. Y = {v1}

• 정점들의 집합이 V에서 해답 정점 집합을 뺸 V - Y에 속한 정점 중에서 v1에서 Y에 속한 정점만을 거쳐 최단 경로가 되는 정점 v를 선정한다.

• 정점 v를 Y에 추가하고 v에서 F로 이어지는 최단 경로 상의 이음선을 F에 추가한다.
  

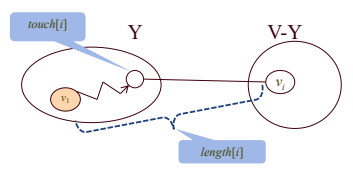
• touch[1..n], length[1..n]의 배열을 유지한다.

  • touch[i] = 현재 단계에서 v로 선정된 정점과 최단 경로로 연결되는 Y에 속한 정점
  • length[i] = Y에 속한 정점들만 중간에 거치도록 하여 v1에서 vi로 가는 현재 최단 경로의 길이
    

pseudo code

분석

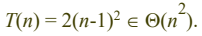
• 힙(heap)으로 구현하면 Θ(m lg n)이고, 피보나찌 힙으로 구현하면 Θ (m + n lg n)이다.

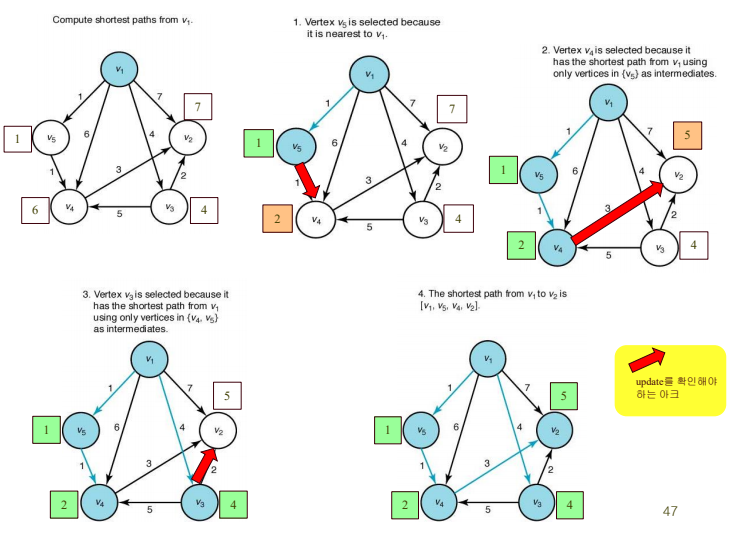
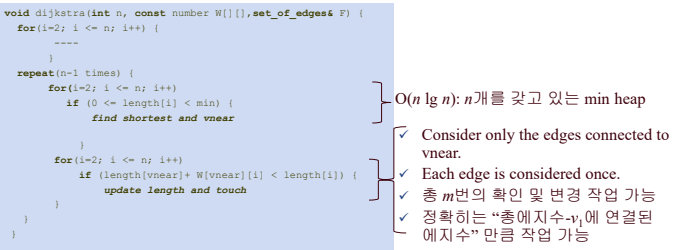
• 최단 경로가 결정될 때마다 출발점에서 해당 정점으로 가는 경로와 최단 경로로 결정된 다른 정점을 거쳐서 가는 경우 중 어느 것이 최단 경로인지 확인해야 한다.

• 총 에지수 - (출발점과 연결된 에지 수) 만큼 최단 경로를 재 확인하는 과정이 필요하다.

python code

inf = 1000

def dijkstra(n, w, f):
    NoC = 0
    touch = [0] * n  # 각 노드로 가는 최단거리는 0번 노드에서 시작합니다.
    length = [0] * n
    for i in range(1, n):
        length[i] = w[0][i]  # 초기 상황에서 최단길이는 0번 노드에서 각 노드로의 길이입니다.
    for i in range(1, n):
        min = inf
        for j in range(1, n):
            if 0 <= length[j] < min:
                min = length[j]
                # length 중 작은 값을 min에 할당합니다.
                # 이미 최단거리가 계산된 node에 대한 거리 값은 -1로 설정되어 있기 때문에
                # 조건문에서 고려되지 않습니다.
                vnear = j
                # 최단거리를 가지는 node 번호를 vnear에 할당합니다.
        f.add((touch[vnear], vnear))
        # 0번 노드에서 각 노드로 가는 최단 경로 중 마지막 노드와 해당 노드의 이음선을
        # f에 추가합니다.

        # Y에 node가 추가됨에 따라 최단 경로의 길이가 수정될 수 있습니다.
        # 0번 노드에서 각 노드로 가는 길이와 Y에 속한 노드를 거쳐 가는 경로 중
        # 더 짧은 거리로 Length를 update합니다.
        for k in range(1, n):
            if length[vnear] + w[vnear][k] < length[k]:
                length[k] = length[vnear] + w[vnear][k]
                touch[k] = vnear
        length[vnear] = -1

        # vnear와 연결된 0번 노드를 제외한 노드의 수를 셉니다.
        for m in range(1, n):
            if m != vnear and w[vnear][m] != inf:
                NoC += 1
    return f, NoC