탐욕적 접근 방법
- 결정의 순간마다 가장 좋다고 생각하는 해답을 선택함으로써 최종적인 해답을 도출하는 방법
- local optimal은 만족하지만 최종적인 global optimal을 만족시킨다는 보장을 없다.
설계 절차
-
선정과정
- 현재 상태에서 가장 좋다고 여겨지는(greedy) 해답을 찾아서 해답 모음에 포함시킨다.
-
적정성 점검
- 새로 얻은 해답 모음이 적절하지 결정한다.
-
해답 점검
- 새로 얻은 해답 모음이 최적의 해인지 결정한다.
spanning tree
- 연결된 비방향성 그래프에서 cycle을 제거하면서 연결된 부분 그래프가 되도록 이음선을 제거함으로써 spanning tree를 만들 수 있다.
- 그래프의 모든 정점을 모두 포함하면서 트리가 되는 연결된 부분 그래프
신장트리의 개수
-
모든 노드 간에 에지가 존재하는 완전 그래프의 경우
- 노드가 n인 완전 그래프의 에지 개수 : nC2
- 트리는 에지 수가 n - 1이다.
- 완전 그래프로부터 생성할 수 있는 에지 수가 n-1인 그래프의 개수는
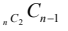
-
그래프가 트리인 경우 : 1개
-
그래프가 순환 그래프인 경우 : n개
-
그래프가 완전 그래프인 경우 : n^(n-2)
-
그래프가 완전 이분 그래프인 경우에는
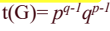
최소비용 신장트리
- 신장트리가 되는 부분 그래프 중에서 가중치가 최소가 되는 부분그래프
- 항상 cycle을 포함하지 않는다.
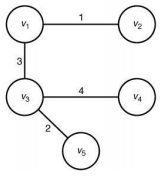
탐욕적 알고리즘을 이용한 최소비용 신장트리 도출
prim 알고리즘
- 시작점에서 가장 최소비용을 가지는 에지와 정점을 해답모음에 추가한다.
- 해답 모음에 추가된 정점을 제외한 정점들 중에서 해답 모음에 포함된 정점에서 가장 적은 비용을 가지는 정점을 해답모음에 추가한다.
- 최소 비용 신장트리 생성 및 사이클 제거
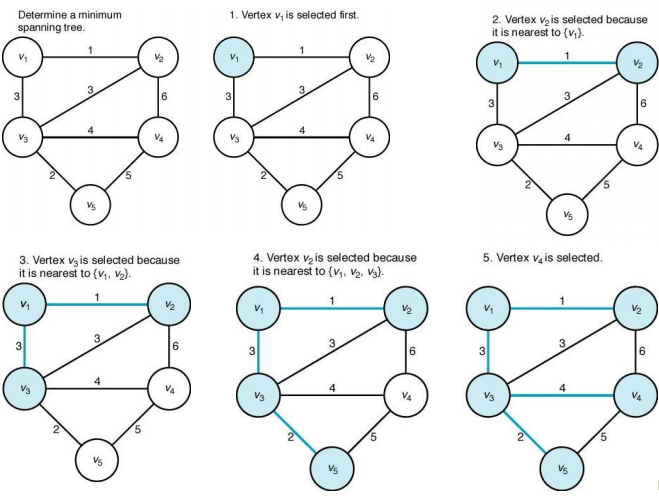
설계 절차
-
그래프의 인접행렬식 표현

-
nearest, distance 배열을 유지한다.
- nearest[i] : Y에 속한 정점 중에서 vi에서 가장 가까운 정점의 인덱스
- distance[1..n] : vi와 nearest[i]를 잇는 이음선의 가중치
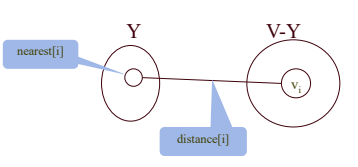
- V - Y에 있는 노드 중 distance[i]를 최소로 하는 i를 vnear로 선정한다.
- vnear가 Y에 편입되며 V - Y에 대하여 distance를 재계산한다.
pseudo code

Kruskal 알고리즘
- 에지의 가중지를 비내림차순으로 정렬한 후 적은 가중치를 가지는 에지와 정점을 해답 모음에 추가한다.
- 추가하고자 하는 이음선과 정점이 사이클을 만든다면 제거한다.
- 모든 정점이 해답모음에 포함되면 알고리즘을 종료한다.
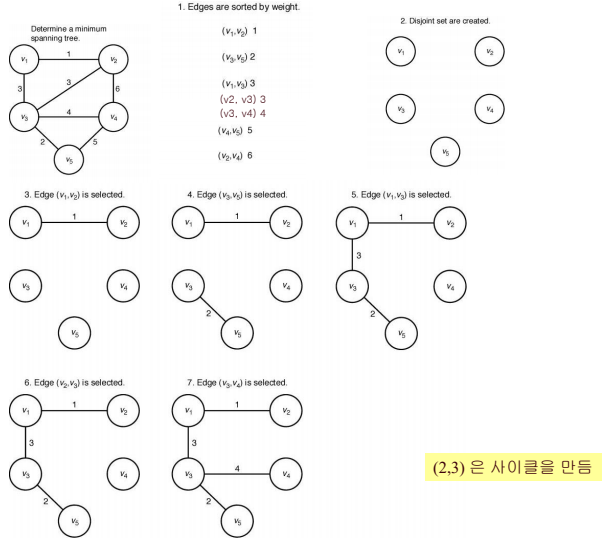
pseudo code

prim 알고리즘 vs. Kruskal 알고리즘

- sparse graph의 경우에는 Kruskal알고리즘이 더 효과적이다.
- dense graph의 경우네는 Prim 알고리즘이 더 효과적이다.
