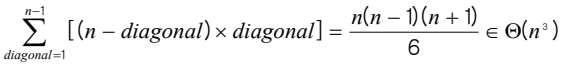연쇄 행렬 곱셈
- i × j 행렬과 j × k행렬을 곱하기 위해서는 i × j × k번 만큼의 곱셈이 필요하다.
- 연쇄적으로 행렬을 곱할 때 어떤 행렬 곱셈을 먼저 수행하느냐에 따라서 필요한 총 곱셈의 횟수가 달라진다.
설계 전략

-
재귀 관계식을 이용하여 이전 단계의 계산을 이후 단계의 계산에 이용한다.
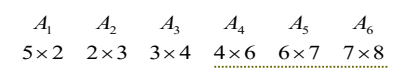

-
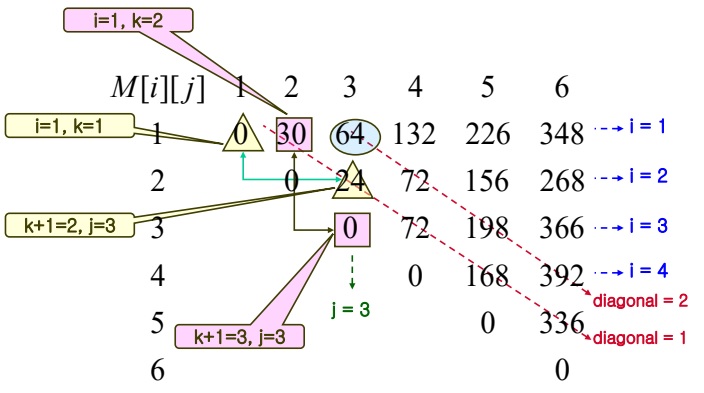
최적 순서를 얻기 위해서 M[i][j]를 계산할 때 최소값을 주는 k값을 P[i][j]에 기록한다.

-
따라서 최종해는 (A1((((A2A3)A4)A5)A6))
pseudo code

python
global index_mat
def printmatrix(mat):
# 행렬의 형태로 출력을 위한 함수
row = len(mat[0])
col = len(mat)
for i in range(row):
for j in range(col):
print(f'{mat[i][j]:>3}', end=' ')
# 복습용) 출력시 행과 열은 맞추기 위한 코드, >3 : 3자리수 오른쪽 정렬
print()
def minmult(n, d):
matrix = [[0 for _ in range(n)] for _ in range(n)]
# n x n 크기의 영행렬을 생성합니다.
# 복습용) numpy를 통한 영행렬 생성시 정수타입이 아니라 매개변수로 사용 제한
for diagonal in range(1, n):
# 주대각성분이 모두 0인 상삼각행렬의 요소를 채우기 위하여
# 1 ~ n-1 까지의 대각선을 선택합니다
for i in range(0, n - diagonal):
# 대각성분이 추가될 행의 index를 i에 저장합니다.
j = i + diagonal
# 대각성분이 추가될 열의 index를 j에 저장합니다.
temp = []
for k in range(i, j):
temp.append(matrix[i][k] + matrix[k + 1][j] + d[i] * d[k + 1] * d[j + 1])
# 구하고자 하는 연쇄행렬 최소곱셈 알고리즘의 행렬의 수가 n이라면,
# 마지막으로 곱할 임의의 행렬 하나와 나머지 행렬 n-1개로 나눕니다.
# 앞서 계산한 값을 바탕으로 n-1 개의 행렬을 구하는데 필요한 최소곱셈의 크기와 마지막으로
# 곱할 행렬에 필요한 크기를 더한 후 temp list에 첨가합니다.
min_k = temp.index(min(temp))
# 최소곱셈이 이루어지는 행렬의 식을 나타내기 위해 가장 작은 크기를 가지는 k의 값을 저장합니다
matrix[i][j] = temp[min_k]
# i번째 행렬에서 j번째 행렬을 곱하는 데 가장 작은 최소곱셈이 되는 값을
# matrix[i][j]에 저장합니다
index_mat[i][j] = min_k + i
# index_mat에 가장 작은 곱셈의 크기를 가지는 k의 값을 저장합니다.
# i행일 때 하삼각행렬의 index가 포함되므로 +i를 해줍니다 ***************
print("가장 작은 곱셈 수행 수")
printmatrix(matrix)
print()
print("가장 작은 곱셈을 수행할 때의 k의 수")
printmatrix(index_mat)
return matrix[0][n - 1]
def order(i, j, index_mat):
ans = ''
if i == j:
print(ans + f'A{i+1}', end='')
# 주대각선을 지칭하면 행렬을 출력합니다
elif i < j:
k = index_mat[i][j]
print(ans + "(", end='')
# 재귀적으로 호출되기 전에 ( 를 출력함으로써
# 주대각선을 지칭하기 전까지 몇번 곱셈이 수행되는지 나타냅니다
order(i, k, index_mat)
# 최소곱셈을 가능케하는 k를 기준으로 이전의 행렬을 바탕으로 다시 재귀적으로 호출합니다
order(k+1, j, index_mat)
# 최소곱셈을 가능케하는 k를 기준으로 이후의 행렬을 바탕으로 다시 재귀적으로 호출합니다
print(ans + ")", end='')
# 재귀적으로 호출이 끝났을 때 )를 출력함으로써 가장 먼저 수행되어야할 곱셈에 ()을 출력합니다.
return ans최소 곱셈 알고리즘의 분석
- 단위 연산 : 각 k값에 대하여 실행된 명령문
- j = i + diagonal이므로 k-루프를 수행하는 횟수 = (j −1) − i +1 = i + diagonal −1− i +1 = diagonal
- for-i 루프를 수행하는 횟수 = n – diagonal