Optimal binary search tree
- 키를 찾는데 걸리는 평균 시간이 최소가 되도록 구축된 트리
data type

- key와 대소 관계와 삽입 선후 관계를 고려한 left/right subtree를 가리키는 nodetype* 이 있다.
이진검색트리의 검색

키의 검색 시간
- depth(key) + 1
- root node는 depth = 0을 지칭하며 key가 있는 tree depth에 1을 더한다.
- notataion :

- 평균 검색 시간 :
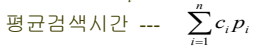
이진검색트리의 개수
- Catalan number :
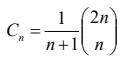
동적계획식 설계전략
- 이전의 계산 결과를 저장한 2차원 배열을 이용하여 효과적인 계산 방법을 사용한다.
- 각 검색 최적 시간을 A[i][j]로 표현한다.
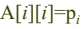
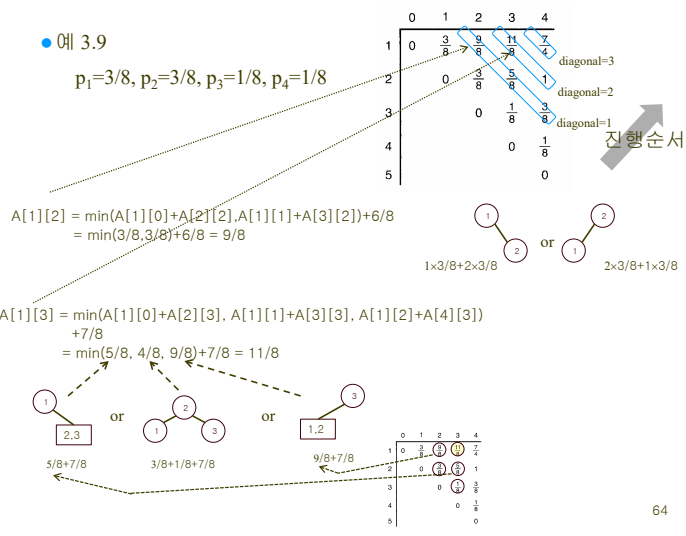
트리 k의 검색 시간
-
트리 k : n개의 키가 있을 때 k번째 키가 루트인 트리
-
검색시간 : A[1][n]

뿌리에서 비교하는데 드는 추가시간은 각각의 left subtree와 right subtree의 루트가 분류된 임의의 아이템이 루트일 경우를 계산한 경우이다. -
최적 이진검색트리의 평균 검색 시간은
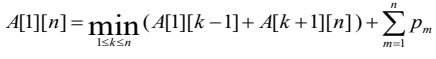
시간복잡도 분석
- 단위연산 : 첨자 k에 대한 문장

pseudo code


- root는 tree(1, n)
python
def printmatrixf(mat):
# 행렬의 형태로 출력을 위한 함수
row = len(mat[0])
col = len(mat)
for i in range(col):
for j in range(row):
print(f'{mat[i][j]:>3.2f}', end=' ')
print()
def printmatrix(mat):
row = len(mat[0])
col = len(mat)
for i in range(col):
for j in range(row):
print(f'{mat[i][j]:>3}', end=' ')
print()
class Node:
def __init__(self, data):
self.data = data
# node의 data를 저장합니다
self.l_child = None
# node의 왼쪽 자식을 지칭합니다.
self.r_child = None
# node의 오른쪽 자식을 지칭합니다.
def tree(key, r, i, j):
k = r[i][j]
if k == 0:
return None
else:
p = Node(key[k])
p.l_child = tree(key, r, i, k - 1)
p.r_child = tree(key, r, k+1, j)
# 루트로 삼은 K보다 작은 것은 왼쪽 자식, 큰 것은 오른쪽 자식을 지칭하며
# 재귀적으로 호출하며 트리구조를 형성합니다.
return p
def optsearchtree(n, p, a, r):
for diagonal in range(1, n):
# 오른쪽 아래로 향하는 대각선이며 주대각선 바로 위의 대각선은 p_i를 의미하며
# diagonal은 p_i를 나타내는 대각선 위를 지칭합니다.
for i in range(1, n - diagonal + 1):
temp = []
sum_prob = 0
j = i + diagonal
for k in range(i, j+1):
temp.append(a[i][k-1] + a[k+1][j])
sum_prob += p[k]
r[i][j] = temp.index(min(temp)) + i
a[i][j] = min(temp) + sum_prob
# 가장 적은 값을 도출하는 요소를 a에 저장하며
# 루트로 삼았을 때 가장 적은 값을 도출하는 루트의 값을 r에 저장합니다.
# 행이 증가할수록 하삼각행렬의 요소도 증가하므로 i를 더해줍니다.
def print_inOrder(root):
if not root:
return None
print_inOrder(root.l_child)
print(root.data)
print_inOrder(root.r_child)
# 왼쪽 자식 -> 부모 -> 오른쪽 자식 순으로 출력합니다
def print_preOrder(root):
if not root:
return None
print(root.data)
print_preOrder(root.l_child)
print_preOrder(root.r_child)
# 부모 -> 왼쪽 자식 -> 오른쪽 자식