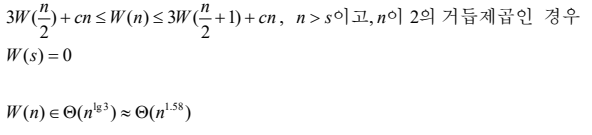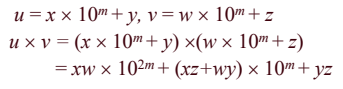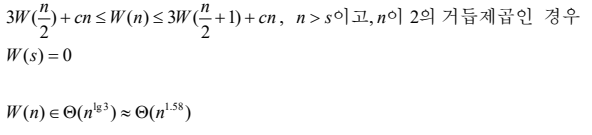Algorithm - 분할정복법 - 큰 정수 계산법

큰 정수 계산법

• 큰 정수의 자리 수를 절반으로 나누고 다음의 공식과 같이 표현하여 계산한다.
• 

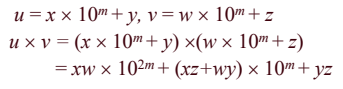
pseudo code

시간복잡도 분석 (최악의 경우)

• 단위연산: 덧셈, 뺄셈, divide 10^m,mod 10^m,×10^m
  

개선된 방법

• 이전 방법에서는 xw, xz + yw, yz의 총 4번의 곱셈 연산이 필요하였다.
• r = (x+y) * (w + z) = xw + (xz + yw) + yz의 계산을 추가함으로써 xz + yw = r - xw - yz로 나타낼 수 있다.
• 결과적으로 덧셈/뺄셈의 연산 횟수는 증가하지만 곱셈은 3회만 필요하다.

pseudo code

python

import math

def prod(num1, num2):
    threshold = 2
    n = max(len(str(num1)), len(str(num2)))
    if num1 == 0 or num2 == 0:  # 두 수 중에 0의 값이 있다면 바로 0을 반환합니다
        return 0
    elif n <= threshold:
        # n이 threshold값이 2보다 작을 경우, 즉 num1, num2가 2자리수 이하 일때는
        # 일반적인 계산방식을 이용하여 값을 반환합니다.
        return num1 * num2
    else:
        m = math.floor(n/2)
        x = num1 // 10**m
        y = num1 % 10**m
        w = num2 // 10**m
        z = num2 % 10**m
        # 큰 수인 num1과 num2를 num1 =  x * (10**m) + y 의 방식으로 자릿수를 기준으로 반으로 나눕니다
        r = prod(x + y, w + z)
        p = prod(x, w)
        q = prod(y, z)
        # 큰 수를 2개로 나눈 것을 기반으로 재귀적으로 호출하며
        # 곱셈 공식인 (ax + b)(cx + d) = acx2 + (ad + bc)x + bd의 꼴로 값을 반환합니다.
        return p * 10**(2*m) + (r - p - q) * 10**m + q

시간복잡도 분석