Quick Sort
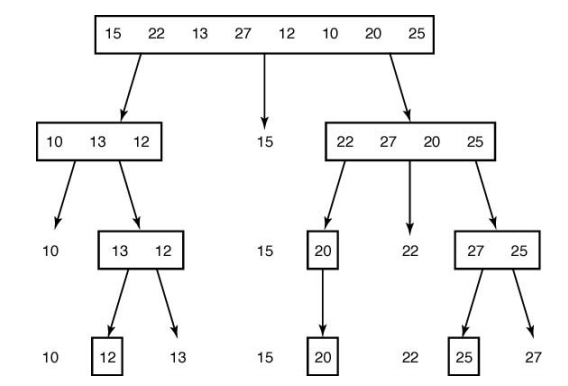
빠른정렬 알고리즘

python - quick sort
def quick_sort(values, first, last):
if first < last:
splitPoint = split(values, first, last)
quick_sort(values, first, splitPoint - 1)
quick_sort(values, splitPoint + 1, last)
return values분할 알고리즘

- j : pivotitem보다 작은 그룹의 제일 우측 끝 데이터 위치를 지칭한다.
- not stable 알고리즘이다. (기존의 데이터 순서가 정렬 후 보존되지 않는 알고리즘)
python - split
def split(values, first, last):
splitval = values[first]
savefirst = first
first += 1
while True:
onCollectSide = True
while onCollectSide:
if values[first] > splitval:
onCollectSide = False
else:
first += 1
onCollectSide = (first <= last)
onCollectSide = (first <= last)
while onCollectSide:
if values[last] <= splitval:
onCollectSide = False
else:
last -= 1
onCollectSide = (first <= last)
if first < last:
temp = values[first]
values[first] = values[last]
values[last] = temp
first += 1
last -= 1
if first <= last:
continue
break
splitPoint = last
temp1 = values[savefirst]
values[savefirst] = values[splitPoint]
values[splitPoint] = temp1
return splitPoint분할 알고리즘 분석
- 단위 연산 : 배열과 pivotitem과의 비교 횟수
- 입력이 비내림차순으로 정렬되어 있을 경우가 최악의 경우이다.
- 기준점보다 작은 항목은 없으므로 크기가 n인 배열은 크기가 0인 부분배열이 왼쪽에 오며 크기가 n-1인 부분배열이 오른쪽에 오도록 계속하여 분할된다.
- T(n) = T(0) + T(n-1) + n - 1
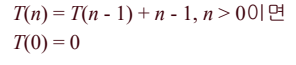
분할 알고리즘 평균의 경우
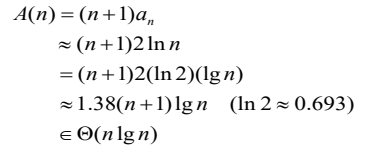
분할 알고리즘 최선의 경우
- 문제가 매번 반씩으로 나누어지는 경우
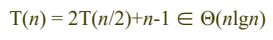
행렬 곱셈
pseudo code

시간복잡도 분석
- 단위연산 : 가장 안쪽의 루프에 있는 곱셈 연산의 횟수
- 모든 경우의 시간복잡도 분석
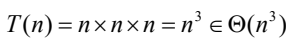
- 단위연산 : 가장 안쪽의 루프에 있는 덧셈 연산의 횟수
- 모든 경우의 시간복잡도 분석
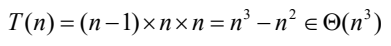
Strassen Method
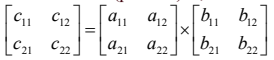
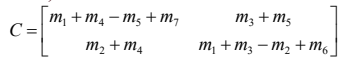
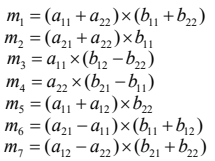
- 행렬의 크기가 커질수록 strassen 방법의 효율성이 높아진다.
pseudo code

- 임계점 : 두 알고리즘의 효율성이 교차하는 문제의 크기
python - Strassen
from numpy import *
import numpy as np
def straseen (n, A, B, C):
threshold = 2
A11 = np.array([[A[rows][cols] for cols in range(int(n / 2))] for rows in range(int(n / 2))])
A12 = np.array([[A[rows][cols] for cols in range(int(n / 2), n)] for rows in range(int(n / 2))])
A21 = np.array([[A[rows][cols] for cols in range(int(n / 2))] for rows in range(int(n / 2), n)])
A22 = np.array([[A[rows][cols] for cols in range(int(n / 2), n)] for rows in range(int(n / 2), n)])
B11 = np.array([[B[rows][cols] for cols in range(int(n / 2))] for rows in range(int(n / 2))])
B12 = np.array([[B[rows][cols] for cols in range(int(n / 2), n)] for rows in range(int(n / 2))])
B21 = np.array([[B[rows][cols] for cols in range(int(n / 2))] for rows in range(int(n / 2), n)])
B22 = np.array([[B[rows][cols] for cols in range(int(n / 2), n)] for rows in range(int(n / 2), n)])
if n <= threshold:
C = np.array(A) @ np.array(B)
else:
M1 = M2 = M3 = M4 = M5 = M6 = M7 = np.array([])
M1 = straseen(int(n/2), (A11+A22), (B11+B22), M1)
M2 = straseen(int(n/2), (A21+A22), B11, M2)
M3 = straseen(int(n/2), A11, (B12-B22), M3)
M4 = straseen(int(n/2), A22, (B21 - B11), M4)
M5 = straseen(int(n/2), (A11+A12), B22, M5)
M6 = straseen(int(n/2), (A21-A11), (B11 + B12), M6)
M7 = straseen(int(n/2), (A12-A22), (B21 + B22), M7)
C = np.vstack( [np.hstack ( [M1+M4-M5+M7, M3+M5] ), np.hstack( [M2+M4, M1+M3-M2+M6] )] )
return C단순 곱셈 방법의 시간복잡도 분석
- T(n): n × n 크기의 행렬 A와 B를 곱하는데 걸리는 시간
- 단위연산: 곱셈하는 연산
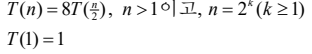
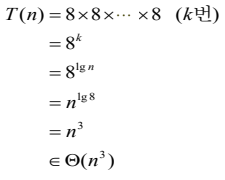
strassen 방법의 시간 복잡도 분석
-
단위연산: 곱셈하는 연산
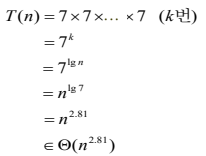
-
단위연산: 덧셈/뺄셈하는 연산
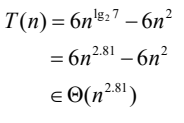
단순 곱셈과 strassen의 비교

