유의성검정

A/B 검정

: 두 버전(A와 B) 중 어느 것이 더 효과적인지 평가하기 위해 사용되는 검정 방법

• 마케팅, 웹사이트 디자인 등에서 많이 사용됨
• 사용자들을 두 그룹으로 나누고, 각 그룹에 다른 버전을 제공한 후, 반응 비교
• 일반적으로 전환율, 구매수, 방문 기간, 방문한 페이지 수, 특정 페이지 방문 여부, 매출등의 지표 비교

목적

• 두 그룹 간의 변화가 우연이 아니라 통계적으로 유의미한지를 확인

• A/B 검정이 실제로 어떻게 적용되는지

  • 온라인 쇼핑몰에서 두 가지 디자인(A와 B)에 대한 랜딩 페이지를 테스트하여 어떤 디자인이 더 높은 구매 전환율을 가져오는지 평가

    		```
    		import numpy as np
    		import scipy.stats as stats
    
    		# 가정된 전환율 데이터
    		group_a = np.random.binomial(1, 0.30, 100)  # 30% 전환율
    		group_b = np.random.binomial(1, 0.45, 100)  # 45% 전환율
    
    		# t-test를 이용한 비교
    		t_stat, p_val = stats.ttest_ind(group_a, group_b)
    		print(f"T-Statistic: {t_stat}, P-value: {p_val}")
    		```

    ❓ stats.ttest_ind
    : scipy.stats.ttest_ind 함수는 독립표본 t-검정을 수행하여 두 개의 독립된 집단 간 평균의 차이가 유의미한지 평가함

    • 이 함수는 두 집단의 데이터 배열을 입력으로 받아서 t-통계량과 p-값을 반환
      • t-통계량 (statistic)
        t-검정 통계량으로 두 집단 간 차이의 크기과 방향을 나타냄
      • p-값 (pvalue)
        p-값은 귀무 가설이 참일때, 현대 데이터보다 극단적인 결과가 나올 확률
        이 값이 유의수준(α) 보다 작으면 직무 가설을 기각하고 이 값이 유의수준(α) 보다 크면 귀무 가설을 기각하지 않음
        ex) 링크텍스트
        링크텍스트
        

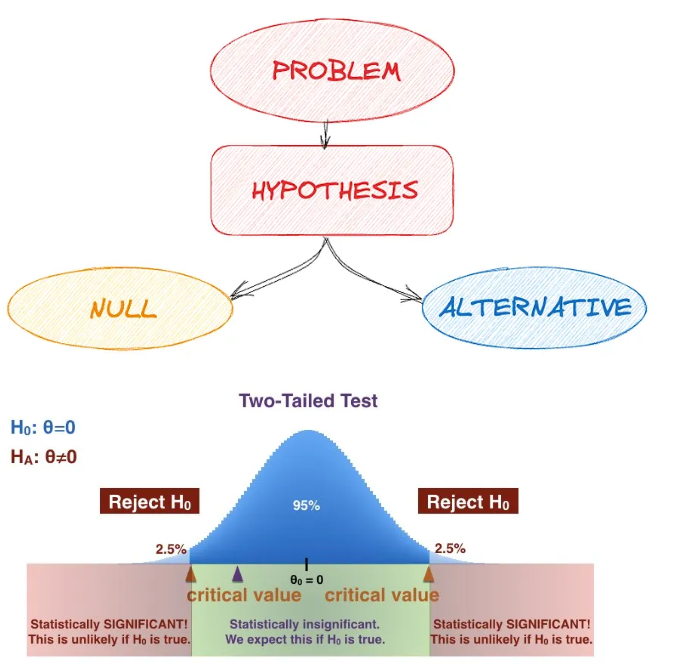
가설검정

링크텍스트
링크텍스트

: 표본 데이터를 통해 모집단의 가설을 검증하는 과정

• 즉, 데이터가 특정 가설을 지지하는지 평가하는 과정
• 귀무가설(H0)과 대립가설(H1)을 설정하고, 귀무가설을 기가할지를 결정
• 데이터 분석시 두가지 전략을 취할 수 있음
  • 확증적 자료분석
    • 미리 가설들을 먼저 세운 다음 가설을 검증해 나가는 분석
  • 탐색적 자료분석 (EDA)
    • 가설을 먼저 정하지 않고 데이터를 탐색해보면서 가설 후보들을 찾고 데이터의 특징을 찾는 것
      ✅ 단계

    1. 귀무가설과 대립가설 설정

    2. 유의수준(α) 결정

    3. 검정통계량 계산

    4. p-값과 유의수준 비교

    5. 결론 도출

       ➡️ 통계적 유의성

    • 통계적 유의성은 결과가 우연히 발생한 것이 아니라 어떤 효과가 실제로 존재함을 나타내는 지표
    • p값은 귀무 가설이 참일 경우 관찰된 통계치가 나올 확률을 의미
    • 일반적으로 p값이 0.05 미만이면 결과를 통계적으로 유의하다고 판단
      ➡️ p-값
    • 귀무가설이 참일 때, 관찰된 결과 이상으로 극단적인 결과가 나올 확률
    • 일반적으로 p-값이 유의수준(α)보다 작으면 귀무가설을 기각
    • 유의수준으로 많이 사용하는 값이 0.05
      ➡️ p-값을 통한 유의성 확인
    • p-값이 0.03이라면, 3%의 확률로 우연히 이러한 결과가 나올 수 있음
    • 일반적으로 0.05 이하라면 유의성이 있다고 봄

신뢰구간과 가설검정

• 신뢰구간과 가설검정은 밀접하게 관련된 개념

• 둘 다 데이터의 모수(ex.평균)에 대한 정보를 구하고자 하는 것이지만 접근 방식이 다름

• 신뢰구간

  • 특정 모수가 포함될 범위를 제공
    → 신뢰구간이란 ?
    모집단의 평균이 특정 범위 내에 있을 것이라는 확률
    일반적으로 95% 신뢰구간이 사용되며, 이는 모집단 평균이 95% 확률로 이 구간 내에 있음을 의미
    만약 어떤 설문조사에서 평균 만족도가 75점이고, 신뢰구간이 70 ~ 80이라면,
    우리는 95% 확률로 실제 평균 만족도가 이 범위 내에 있다고 말할 수 있음

• 가설검정

  • 모수가 특정 값과 같은지 다른지 테스트
    ex) 새로운 약물이 기존 약물보다 효과가 있는지 검정
    ✅ 이 때 새로운 약물은 기존 약물과 큰 차이가 없다는 것이 귀무가설
    ✅ 대립가설은 새로운 약물이 기존 약물과 대비해 효과가 있다는 것
    = 귀무가설은 현재 상태를 나타내며, 대립가설은 연구자가 입증하고자 하는 주장

  		# 기존 약물(A)와 새로운 약물(B) 효과 데이터 생성
  		A = np.random.normal(50, 10, 100)
  		B = np.random.normal(55, 10, 100)
  	
  		# 평균 효과 계산
  		mean_A = np.mean(A)
  		mean_B = np.mean(B)
  	
  		# t-검정 수행
  		t_stat, p_value = stats.ttest_ind(A, B)
  	
          print(f"A 평균 효과: {mean_A}")
          print(f"B 평균 효과: {mean_B}")
          print(f"t-검정 통계량: {t_stat}")
          print(f"p-값: {p_value}")
  
          # t-검정의 p-값 확인 (위 예시에서 계산된 p-값 사용)
          print(f"p-값: {p_value}")
          if p_value < 0.05:
              print("귀무가설을 기각합니다. 통계적으로 유의미한 차이가 있습니다.")
          else:
              print("귀무가설을 기각하지 않습니다. 통계적으로 유의미한 차이가 없습니다.")
  			```

t검정

가설검정의 대표적인 검정

t검정

: 두 집단 간의 평균 차이가 통계적으로 유의미한지 확인하는 검정 방법

• 독립표본 t검정과 대응표본 t검정으로 나뉨

독립표본 t검정

: 두 독립된 그룹의 평균을 비교

대응표본 t검정

• 동일한 그룹의 사전/사후 평균을 비교

• 가설검정이 실제로 어떻게 적용되는지

  • p-값을 통한 유의성 확인

    • 두 클래스의 시험 성적 비교(독립표본 t검정)
    • 다이어트 전후 체중 비교(대응표본 t검정)

    			# 학생 점수 데이터
    scores_method1 = np.random.normal(70, 10, 30)
    scores_method2 = np.random.normal(75, 10, 30)
    
    # 독립표본 t검정
    t_stat, p_val = stats.ttest_ind(scores_method1, scores_method2)
    print(f"T-Statistic: {t_stat}, P-value: {p_val}")
    			```

다중검정

여러 가설을 동시에 검정 🚫 하지만 오류가 발생할 수 있음

다중검정

: 여러 가설을 동시에 검정할 때 발생하는 문제

• 각 검정마다 유의수준을 조정하지 않으면 1종 오류(귀무가설이 참인데 기각하는 오류)발생 확률이 증가

보정 방법

• 본페로니 보정, 튜키 보정, 던넷 보정, 윌리엄스 보정 등이 있음

• 가장 대표적이고 기본적인게 본페로니 보정

  • 다중검정과 보정을 어떻게 적용하는지
  • 이 때 본페로니 보정을 사용해볼 수 있음

  import numpy as np
  import scipy.stats as stats
  
  # 세 그룹의 데이터 생성
  np.random.seed(42)
  group_A = np.random.normal(10, 2, 30)
  group_B = np.random.normal(12, 2, 30)
  group_C = np.random.normal(11, 2, 30)
  
  # 세 그룹 간 평균 차이에 대한 t검정 수행
  p_values = []
  p_values.append(stats.ttest_ind(group_A, group_B).pvalue)
  p_values.append(stats.ttest_ind(group_A, group_C).pvalue)
  p_values.append(stats.ttest_ind(group_B, group_C).pvalue)
  
  # 본페로니 보정 적용
  alpha = 0.05
  adjusted_alpha = alpha / len(p_values)
  
  # 결과 출력
  print(f"본페로니 보정된 유의 수준: {adjusted_alpha:.4f}")
  for i, p in enumerate(p_values):
      if p < adjusted_alpha:
          print(f"검정 {i+1}: 유의미한 차이 발견 (p = {p:.4f})")
      else:
          print(f"검정 {i+1}: 유의미한 차이 없음 (p = {p:.4f})")

카이제곱검정

범주형 데이터의 분석에 사용한다는 것이 포인트

카이제곱검정

• 범주형 데이터의 표본 분포가 모집단 분포와 일치하는지 검정(적합도 검정)하거나
• 두 범주형 변수 간의 독립성을 검정(독립성 검정)

적합도 검정

• 관찰된 분포와 기대된 분포가 일치하는지 검정
• p값이 높으면 데이터가 귀무 가설에 잘 맞음 즉, 관찰된 데이터와 귀무 가설이 적합
• p값이 낮으면 데이터가 귀무 가설에 잘 맞이 않음 즉, 관찰된 데이터와 귀무 가설이 부적합

독립성 검정

• 두 범주형 변수 간의 독립성을 검정

• p값이 높으면 두 변수 간의 관계가 연관성이 ❌ → 독립성 ⭕

• p값이 낮으면 두 변수 간의 관계가 연관성이 ⭕ → 독립성 ❌

  • 카이제곱검정은 어떻게 적용되는지

    • 범주형 데이터의 분포 확인 및 독립성 확인을 위해 사용

      • 주사위의 각 면이 동일한 확률로 나오는지 검정(적합도 검정)
      • 성별과 직업 만족도 간의 독립성 검정(독립성 검정)

      # 적합도 검정
      observed = [20, 30, 25, 25]
      expected = [25, 25, 25, 25]
      chi2_stat, p_value = stats.chisquare(observed, f_exp=expected)
      print(f"적합도 검정 카이제곱 통계량: {chi2_stat}, p-값: {p_value}")
      
      # 독립성 검정
      observed = np.array([[10, 10, 20], [20, 20, 40]])
      chi2_stat, p_value, dof, expected = stats.chi2_contingency(observed)
      print(f"독립성 검정 카이제곱 통계량: {chi2_stat}, p-값: {p_value}")
      
      # 성별과 흡연 여부 독립성 검정
      observed = np.array([[30, 10], [20, 40]])
      chi2_stat, p_value, dof, expected = stats.chi2_contingency(observed)
      print(f"독립성 검정 카이제곱 통계량: {chi2_stat}, p-값: {p_value}")

      • stats.chisquare 함수 ❓
        • scipy.stats.chisquare 함수는 카이제곱 적합도 검정을 수행하여 관찰된 빈도 분포가 기대된 빈도 분포와 일치하는지 평가함
          이 검정은 주로 단일 표본에 대해 관찰된 빈도가 특정 이론적 분포(예: 균등 분포)와 일치하는지 확인하는 데 사용
        • 반환 값
          • chi2: 카이제곱 통계량입니다.
          • p: p-값입니다. 이는 관찰된 데이터가 귀무 가설 하에서 발생할 확률입니다.
      • stats.chi2_contingency 함수 ❓
        • scipy.stats.chi2_contingency 함수는 카이제곱 검정을 수행하여 두 개 이상의 범주형 변수 간의 독립성을 검정함
          이 함수는 관측 빈도를 담고 있는 교차표(contingency table)를 입력으로 받아 카이제곱 통계량, p-값, 자유도, 그리고 기대 빈도(expected frequencies)를 반환
        • 반환 값
          • chi2 : 카이제곱 통계량입니다.
          • p : p-값입니다. 이는 관측된 데이터가 귀무 가설 하에서 발생할 확률
          • dof : 자유도입니다. 이는 (행의 수 - 1) * (열의 수 - 1)로 계산
          • expected : 기대 빈도
            이는 행 합계와 열 합계를 사용하여 계산된 이론적 빈도

제 1종 오류와 제 2종 오류

두가지의 오류를 구분하는 것이 포인트

제 1종 오류

• 귀무가설이 참인데 기각하는 오류
• 잘못된 긍정을 의미 (아무런 영향이 없는데 영향이 있다고 하는 것)
• 한 단어로 위양성
• α를 경계로 귀무가설을 기각하기 때문에 제1종 오류가 α만큼 발생
• 따라서 유의수준(α)을 정함으로써 제 1종 오류 제어 가능
• 만약, 유의수준이 0.05라면 100번 중 5번정도 일어날 수 있는 제 1종 오류는 감수하겠다는 것
  • 다중 검정시 제 1종 오류가 증가하는 이유 ❓
    • 하나의 검정에서 제 1종 오류가 발생하지 않을 확률은 1 - α
    • m개의 독립된 검정에서 제1종 오류가 전혀 발생하지 않을 확률은 $(1-\alpha)^{m}$
    • 따라서, m개의 검정에서 하나 이상의 제1종 오류가 발생할 확률(즉, 전체 제 1종 오류율)은 $1-(1-\alpha)^{m}$
    • 이 값은 m이 커질수록 빠르게 증가함
      ex) α=0.05, m=10인 경우
      $1-(1-0.05)^{10} \approx 0.401$
    • 즉, 10개의 가설을 동시에 검정할 때 하나 이상의 가설에서 제 1종 오류가 발생할 확률이 약 40.1% 이므로 개별검증에서 발생하는 오류율(5%)보다 높음

제 2종 오류

• 귀무가설이 거짓인데 기각하지 않는 오류
• 잘못된 부정을 의미 ( 영향이 있는데 영햐잉 없다고 하는 것 )
• 한 단어로 위음성
• 제 2종 오류가 일어날 확률은 β로 정의
• 제 2종 오류가 일어나지 않을 확률은 검정력(1-β)으로 정의
• 하지만 이를 직접 통제할 수는 없음
• 그나마 통제를 해볼 수 있는 방법으로는…
  • 표본크기 n이 커질 수록 β가 작아짐
  • α와 β는 상충관계에 있어서 너무 낮은 α를 가지게 되면 β는 더욱 높아짐

예시

• 새로운 약물이 효과가 없는데 있다고 결론 내리는 것 (제 1종 오류)
• 효과가 있는데 없다고 결론 내리는 것 (제 2종 오류)

연습문제

(난 도움이 많이 됬기때문에)

1. 가설검정에서 사용되는 주요 개념 중 하나인 p-value의 의미를 설명하세요.
   p-value는 귀무가설이 참일 때, 관찰된 데이터 또는 더 극단적인 데이터가 나타날 확률이다.

2.가설검정에서 귀무가설(null hypothesis)과 대립가설(alternative hypothesis)의 차이에 대한 설명으로 옳은 것을 고르세요.
귀무가설은 현재 상태를 나타내며, 대립가설은 연구자가 입증하고자 하는 주장이다.

3. 두 그룹의 평균이 서로 다른지 비교하기 위해 사용되는 t검정의 종류는 무엇인가요?
   독립 표본 t검정

4.다중검정에서 발생할 수 있는 문제점은 무엇인가요?
여러 번의 검정을 수행할 때, 전체 실험에서 제 1종 오류가 발생할 확률이 증가한다.

5. 카이제곱검정은 주로 어떤 데이터를 분석할 때 사용되나요?
   범주형 데이터

6. 제 1종 오류(Type I error)와 제 2종 오류(Type II error)의 차이에 대한 설명으로 옳은 것을 고르세요.
   제 1종 오류는 귀무가설이 참인데 기각하는 오류이고, 제 2종 오류는 대립가설이 참인데 기각하는 오류이다.