모집단
: 궁극적으로 관심있는 집단, 모집단의 특징을 모수라 함
ex) 인구 총조사
표준 집단
: 모집단에서 특정한 방법을 이용하여 뽑아낸 임의의 집단, 특징들을 통계량이라 함
ex) 미국대선 출구조사
- 모집단을 모두 전수조사하여 기술통계를 하면 정확한 값을 얻을 수 있지만 비용의 한계로 수행하지 못하는 경우에 "대표성"있는 샘플을 추출하여 이를 추론하는 것이 목적

표본 추출의 중요성
- 샘플링 편향(Sampling bias) : 분석 대상이 표본을 선택할 떄 과대하게 대표되거나 반대의 경우
- 1936년 미국대선 당시 민주당 루즈벨트 vs 공화당 랜던의 경선
- 1000만명이 넘는 사람으로부터 대선 설문 조사 진행 → 공화당 랜던 승리 예측
- 갤럽은 겨우 2000명을 대상으로 격주로 여론 조사 실시 → 민주당 루즈벨트 승리 예상
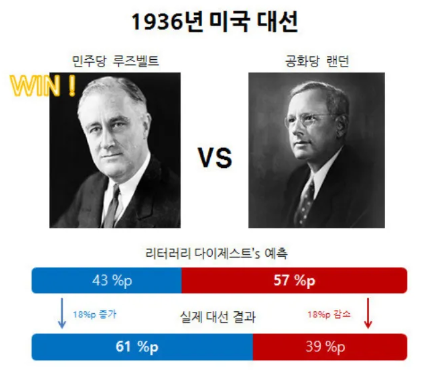
- why ?
- 다이제스트 사 : 자동차와 전화번호의 기록으로 설문조사 진행
→ 실제로 두 제품은 부유층(즉 공화당 지지자들 다수)의 소유물 - 결과적으로 다이제스트사는 망하고 갤럽이 여론조사의 대표 회사로 자리매김
- 다이제스트 사 : 자동차와 전화번호의 기록으로 설문조사 진행
이처럼 편향을 없애기 위한 다양한 표본추출 방법이 있다 링크텍스트
정규분포의 중요성
- 데이터 분석에 대한 피라미드
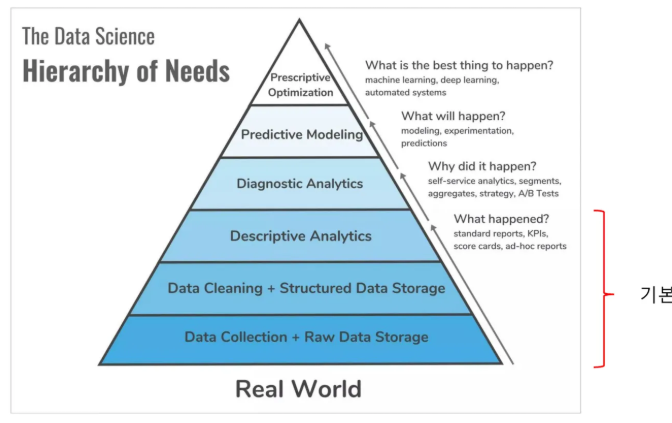
- 통계학의 대표적인 방법론은 1️⃣기술통계와 2️⃣추론통계
- 기술통계가 데이터의 특징을 요모조모보는 과정이라면, 추론통계는 표본으로부터 모집단을 추정하는 과정
- 이 추론통계를 하려면 기반이 있어야 하는데 이것이 바로 분포 그리고 가장 기반을 많이 두는 것이 정규분포
분포
: 데이터가 특정 값 중심으로 흩어진 형태를 나타내는 통계적 개념이며 경험적인 데이터의 형태
1. 이산확률분포
2. 연속확률분포
- 장점
- 데이터의 요약(중앙값, 평균, 분산)등에 대한 수식 표현 가능
- 모집단을 추정하는 가설의 기반
- 각 분포는 특정 확률 함수를 가지며 이를 통해 예측이 가능
- 분포를 형태 현상을 모델링할 수 있음
( 모델링 : 현실 세계를 추상화, 단순화, 명확화하는 방법)
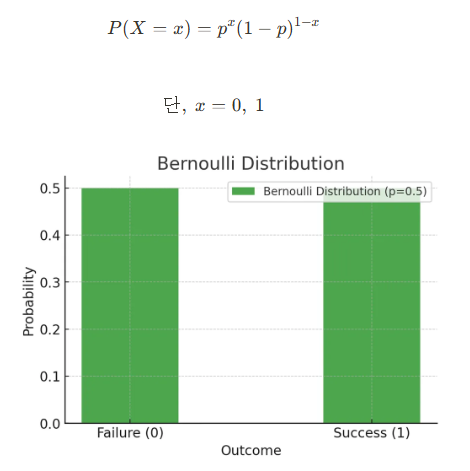
베르누이 분포
: 확률 변수가 취할 수 있는 경우가 2가지인 경우 ( ex:동전 던지기, 클릭 등 )
( 확률 : 0과 1사이 값이며 모든 경우 확률의 합은 1
확률 변수 : 변수가 가질 수 있는 경우의 수를 표현하는 방법)
- 어떤 유저가 웹페이지를 방문하여 버튼을 클릭할 경우가 1, 않는 경우가 0가 동등하다고 생각하면 다음과 같이 표현

- 일반화 수식
이항 분포
-
여러 유저가 입장하는 경우는 어떻게 표현할 수 있을까? 이때 등장하는 것이 사건(경우의 수)
-
베르누이 분포의 n번 확장 버전
ex) 유저 3명이 웹페이지를 방문했을 때 2명이 버튼을 클릭할 경우는
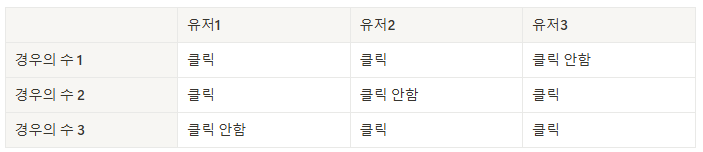
-
이항분포 표현식

-
이항분포 수식

-
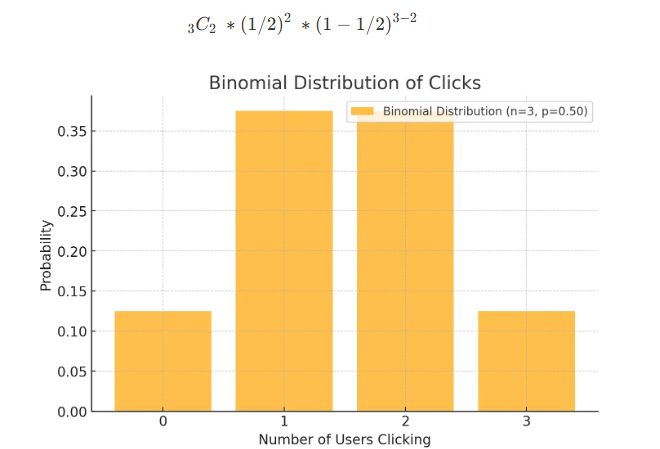
3명의 유저가 버튼을 클릭할 확률이 1/2일 때, 2명의 유저가 클릭할 확률은
- n = 3, k = 2, p = 1/2
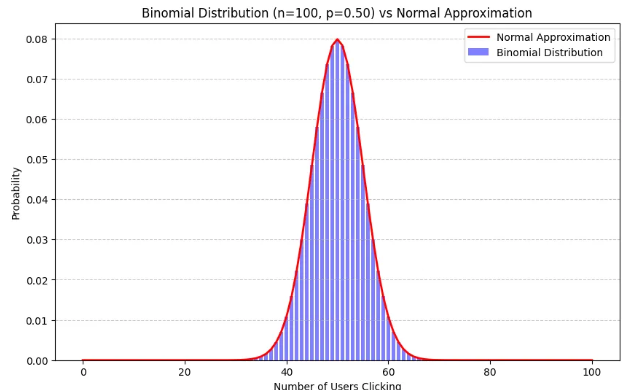
만약 n이 커지면 어떻게 될까? 자연스럽게 정규분포의 모양과 비슷해짐
일반적으로 np>5 이면서 n(1-p) >5인 경우 정규분포를 따른다고 "경험적"으로 알려짐
- n = 3, k = 2, p = 1/2
-
이를 수식으로 표현한다면
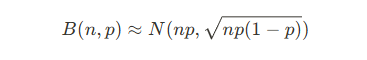
==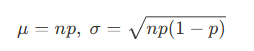
균등 분포
: 모든 x에 대해서 확률이 동일한 분포
- 연속확률 분포 중 하나
이론적으로 주사위는 균등 분포의 유사한 사례긴하지만, 이산확률이기 때문에 정확한 비유는 못 됩니다요
정규분포
: 평균을 기준으로 좌우 대칭이며, 종 모양으로 봉우리가 1개인 연속확률 분포
- 정규분포의 장점은 평균과 표준편차를 알고있으면 전체 데이터의 몇 % 포함되는지 알 수 있다
- 정규분포 표현식
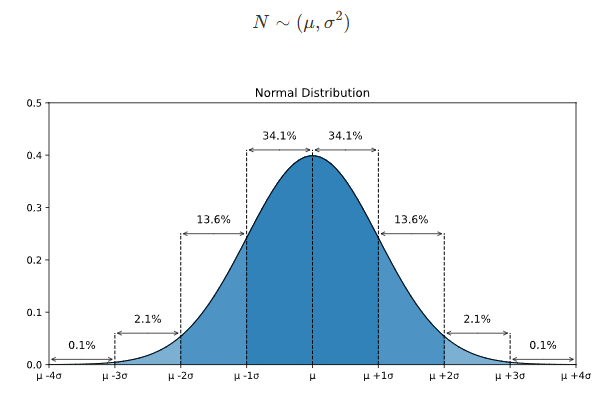
- : 전체 데이터의 68%
- : 전체 데이터의 95%
- : 전체 데이터의 99.7%
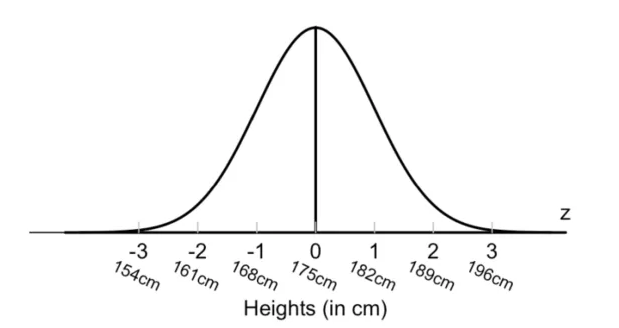
ex) 20대 남자의 키 분포
20대의 경우에는 :
- 정규분포 표현식
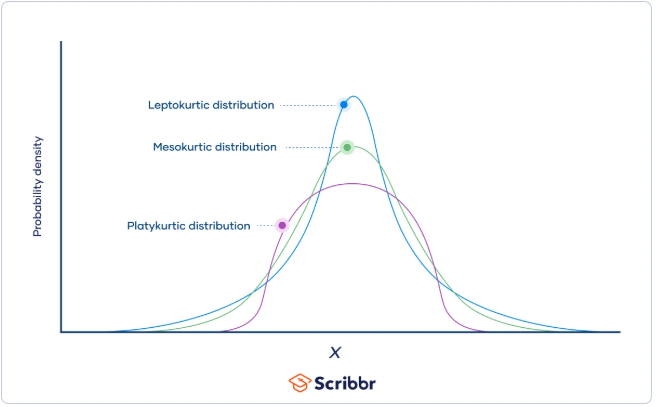
왜도와 첨도
왜도 : 확률의 비대칭 정도를 나태나는 측도
- 긴꼬리 분포라고도 하며 보통 결제 금액, 원급과 같은 수치가 right skewness 특성을 띔
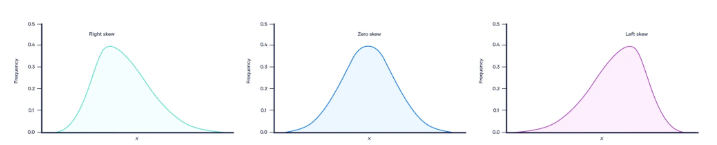
첨도 : 종모양의 뾰족한 정도를 나타내는 측도 - 첨도가 정규분포보다 낮으면 뭉특한 모양으로 이상치가 적으며
- 첨도가 정규분포보다 높으면 꼬리가 길고 이상치가 많다
표준정규분포
매번 다른 측정 값들 (몸무게, 키, 발 사이즈) 등을 데이터를 수집하기보다는 일관된 하나의 분포로 계산하길 원했다 이때 등장한 것이 표준정규분포이고, 통계학자들은 표준정규분포를 만든 뒤 모든 확률에 대해서 계산해놓았음
-
표준정규분포: $\mu = 0,\sigma = 1 $ 인 정규분포
- 달성하기 위하여 모든 데이터에 대해서 "정규화"를 수행
→ 정규화는 어떤 대상을 규칙이나 기준에 따른 상태를 만드는 방법
추론통계에서는 "모든 데이터에서 평균을 빼고 표준편차를 나누는 방법"을 말함
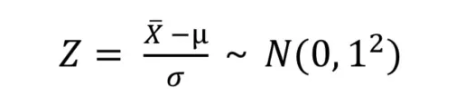
- 달성하기 위하여 모든 데이터에 대해서 "정규화"를 수행
-
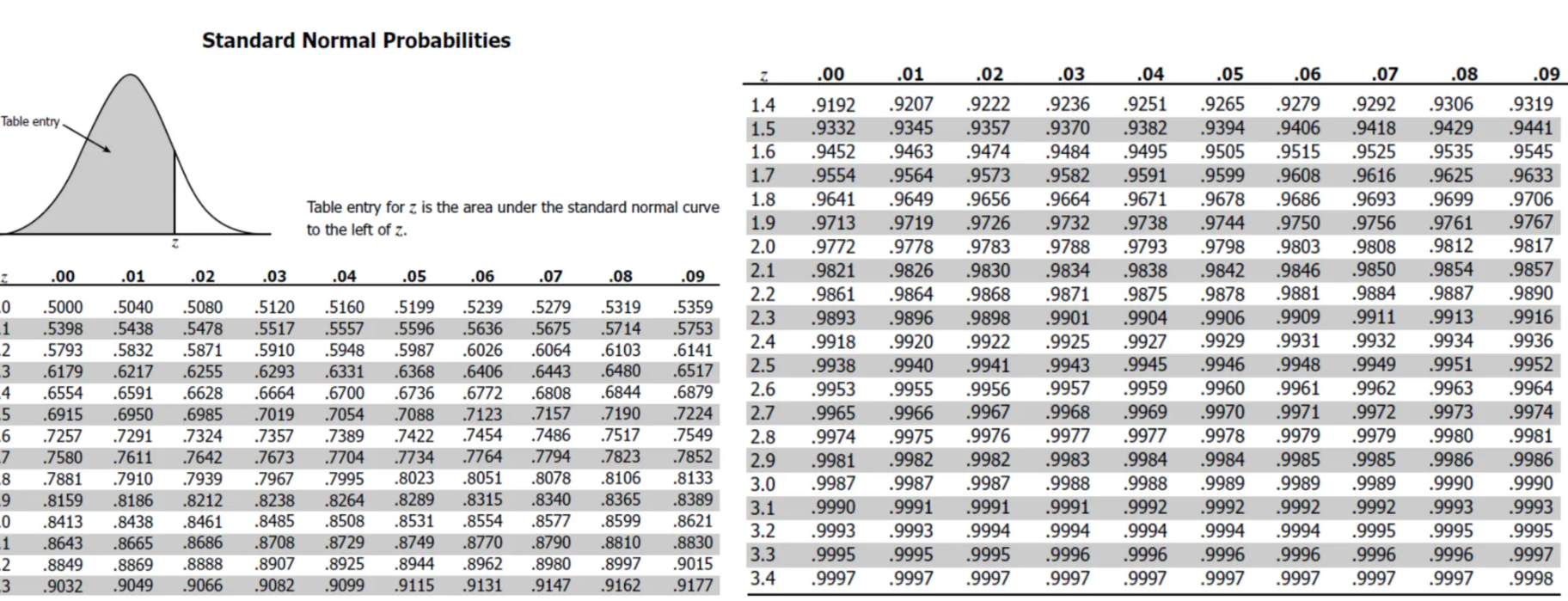
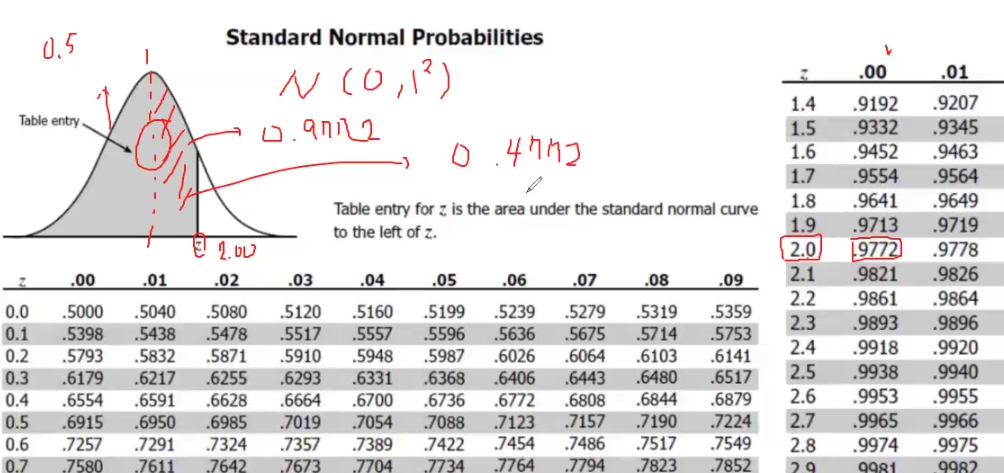
또한 모든 z 값에 대해서 계산해놓은 표가 존재하는데 이를 표준정규분포표 라고 함
-
하기 표는 z값의 왼쪽 끝 ( ) 부터 해당하는 z 값까지 "누적된 확률값" 을 제공
✅
Scipy 모듈
: Scipy 는 Science + Python의 의미로 말 그대로 공학, 사회과학 등에 자주 사용하는 기초통계 모듈과 함수를 모아 놓은 라이브러리
- 자주 쓴느 라이브러리
scipy
│
├── stats # 통계 분석과 확률 분포 관련 함수 제공
│ ├── norm # 정규분포 관련 함수 (PDF, CDF, 랜덤 샘플링 등)
| |── uniform # 균등분포
| |── bernoulli # 베르누이 분포
| |── binom # 이항분포
│ ├── ttest_ind # 독립 두 표본에 대한 t-검정
│ ├── ttest_rel # 대응표본 t-검정
│ ├── mannwhitneyu # Mann-Whitney U 비모수 검정
│ ├── chi2_contingency # 카이제곱 독립성 검정
│ ├── shapiro # Shapiro-Wilk 정규성 검정
│ ├── kstest # Kolmogorov-Smirnov 검정 (분포 적합성 검정)
│ ├── probplot # Q-Q plot 생성 (정규성 시각화)
│ ├── pearsonr # Pearson 상관계수 계산
│ ├── spearmanr # Spearman 순위 상관계수 계산
│ └── describe # 기술 통계량 제공 (평균, 표준편차 등)- 대부분 stats 모듈쪽에 분포관련된 함수들이 존재
- 일반적으로 경로는 scipy.stats.(분포이름).(메소드) 의 규칙을 따름
