데이터 분석으로 할 수 있는 일
기술통계/시각화 : 데이터 명확하게 보기
추론통계 : 수집된 데이터를 기반으로 진짜 그 사실이 맞나? 확인
머신러닝/딥러닝 : 알고리즘에 기대어 결과를 예측하거나 새로운 정보 도출
통계학 도구
- Excel
- SAS
- R
- Python
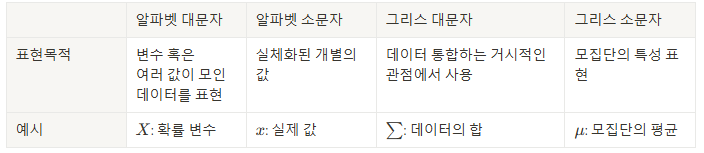
수식
자료형의 종류
범주형 자료
- 명목형 자료 : 순서가 의미 없는 자료 (ex : 혈액형 A, B, O, AB)
- 순서형 자료 : 순서가 의미 있는 자료 (ex : 학점 A, B, C)
수치형 자료
- 이산형 자료 : 두 데이터 구간이 유한한 자료 (ex : 1명,2명)
- 연속형 자료 : 두 데이터 구간이 무한한 자료 (ex : 키 160 ~ 170)
범주형 자료는 인간의 언어로 표현된 자료이기 때문에 컴퓨터 혹은 수식에 적용할 때는 반드시 숫자형으로 변형하여 전달해야 함
computer science에서는 이를 인코딩 방법을 이용함
: 인코딩(encoding) : 어떤 정보를 정해진 규칙에 따라 변환하는 것
중심경향치
‣ 범주형의 요약은 최빈값을 이용할 수 있음 (가장 많이 등장하는 값)
‣ 수치형의 경우 평균(mean), 중앙값(median)이 사용
-
평균

평균은 이상치에 민감함
이상치 : 데이터의 형태에 크게 벗어나느 값을 의미하며, 통계적방법과 도메인 지식을 사용하여 삭제를 고려해볼 수 있음 -
중앙값
‣ 일련의 숫자를 값 순서대로 줄 세웠을 때, 백분위 50%에 해당하는 값
‣ 이상값이 존재하는 경우에도 집단의 대표성을 설명할 수 있음
산포도
‣ 데이터의 퍼짐 정도를 나타내는 방법
‣ IQR(Inter Quantile Range) : 백분위 기준 75%(Q3)와 백분위 기준 25%(Q1)의 차이
- 분산
- 평균에 데이터가 퍼진 정도
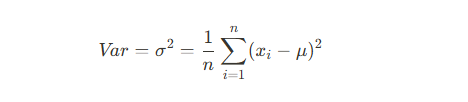
- 10, 20, 30, 40, 50의 분산
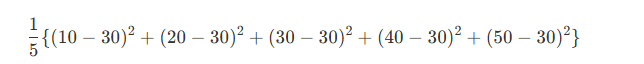
```import numpy as np data = [10,20,30,40,50] my_array = np.array(data) np.var(my_array) ''' 200 '''
- 평균에 데이터가 퍼진 정도
- 표준편차
- 분산의 제곱근
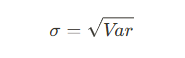
- 변동계수
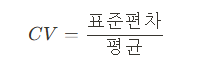
- 서로 값의 스케일이 다르면 분산도 달라짐
- 이를 보정하기 위한 방법
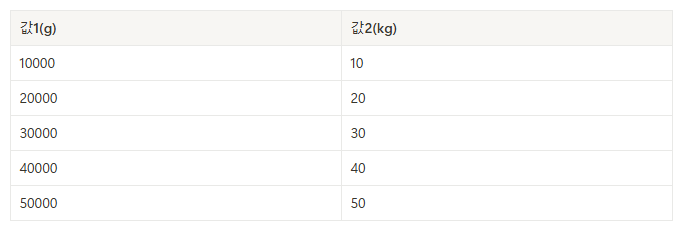
- 값1의 포준편자는 14142, 값2의 표준편차는 14
- 둘의 값 스케일이 달라 일어나는 문제 이를 보완하기 위한 변동계수
- 값 1의 변동계수
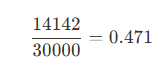
- 값 2의 변동계수
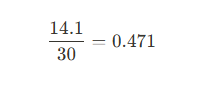
- 분산의 제곱근
Numpy 모듈
- numpy는 다차원 배열을(ex: 행렬) 쉽게 처리해주는 모듈 중 하나
- 특히 통계학 및 데이터사이언스에서는 "선형대수"라는 학문을 탐구할 때 사용
- python은 기본적으로 편의성과 효율성을 교환환 언어, 속도가 느린 점을 보완하여 수학적 계산은 numpy를 자주 활용
- pandas의 기반 언어가 numpy이기 때문에 서로 호환되는 함수/메소드가 많음
자주 쓰는 함수
numpy
│
├── 기본 통계 함수
│ ├── mean() # 데이터의 평균값 계산
│ ├── median() # 데이터의 중앙값 계산
│ ├── std() # 데이터의 표준편차 계산
│ ├── var() # 데이터의 분산 계산
│ ├── sum() # 데이터의 합계 계산
│ ├── prod() # 데이터의 곱 계산
│
├── 퍼센타일 및 백분위 함수
│ ├── percentile() # 데이터의 특정 퍼센타일 값 계산
│ ├── quantile() # 데이터의 특정 분위 값 계산
│
├── 최소값/최대값 관련 함수
│ ├── min() # 데이터의 최소값 반환
│ ├── max() # 데이터의 최대값 반환
│ ├── argmin() # 최소값의 인덱스 반환
│ ├── argmax() # 최대값의 인덱스 반환
│
├── 데이터 생성 및 처리 함수
│ ├── histogram() # 데이터의 히스토그램 계산
│ ├── unique() # 데이터에서 고유 값 반환
│ ├── bincount() # 정수 배열의 값의 빈도 계산
│
├── 랜덤 데이터 생성 (통계적 실험 시 사용 가능)
│ ├── random.randn() # 표준 정규분포를 따르는 랜덤 값 생성
│ ├── random.normal() # 정규분포를 따르는 랜덤 값 생성
│ ├── random.randint() # 정수 범위에서 랜덤 값 생성
│ ├── random.choice() # 데이터에서 랜덤 샘플 추출numpy의 사용 이유
- array형 자료형을 선언하여 관리
a. 리스트에는 존재하지 않는 기술통계량 사용 가능
b. 데이터 처리 속도가 매우 빠름
-
10000개의 리스트 요소에 각 10을 더할때
``` # list으로 처리 import time start = time.time() my_list = [i for i in range(10000000)] for i in range(len(my_list)): my_list[i] = my_list[i] + 10 end = time.time() print(end - start)# array 자료형으로 처리 import numpy as np start = time.time() np.array(my_list) + 10 end = time.time() print(end-start) ``` -
random 모듈을 사용할 수 있음
- 이는 데이터를 임의로 만들어 시뮬레이션 할 수 있음
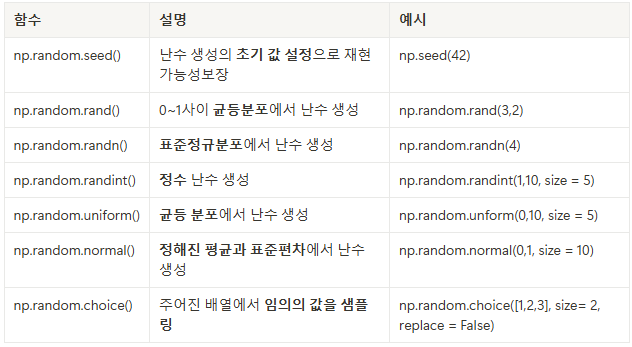
- 이는 데이터를 임의로 만들어 시뮬레이션 할 수 있음
