다이나믹 프로그래밍


다이나믹 프로그래밍의 조건

피보나치 수열

이도 dp를 통해서 구할 수 있다.
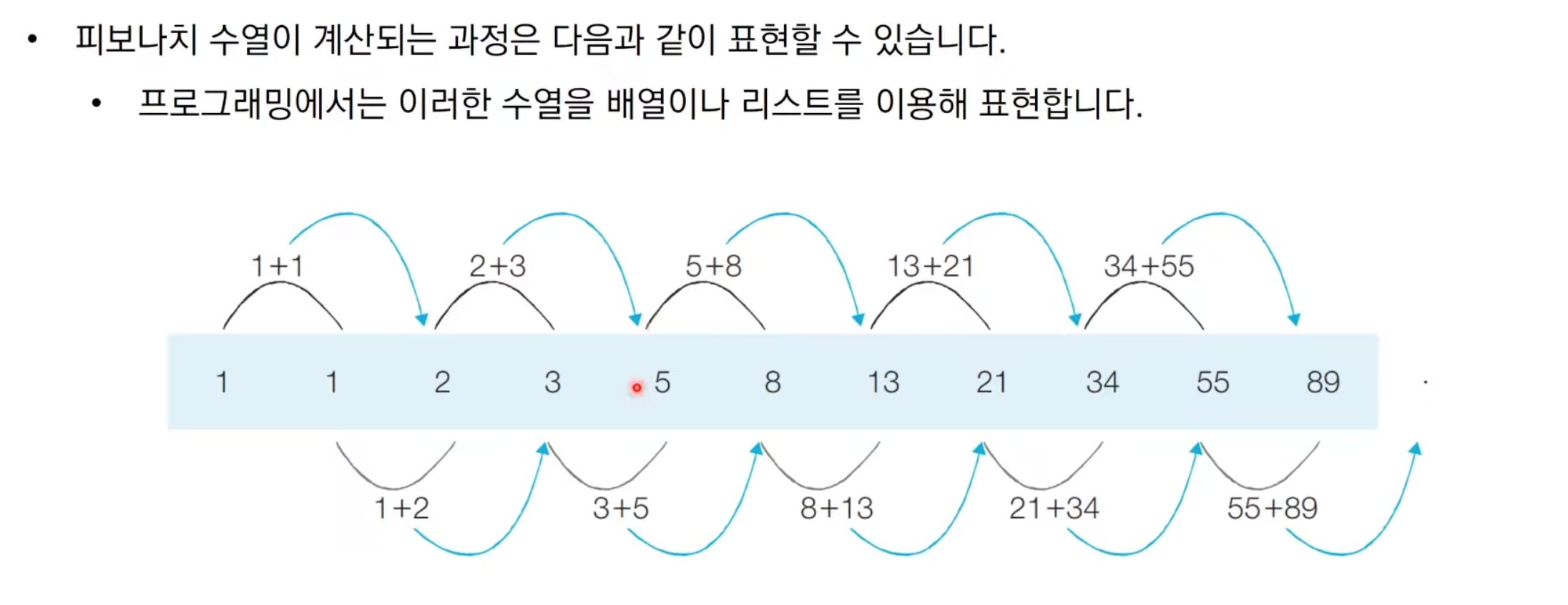
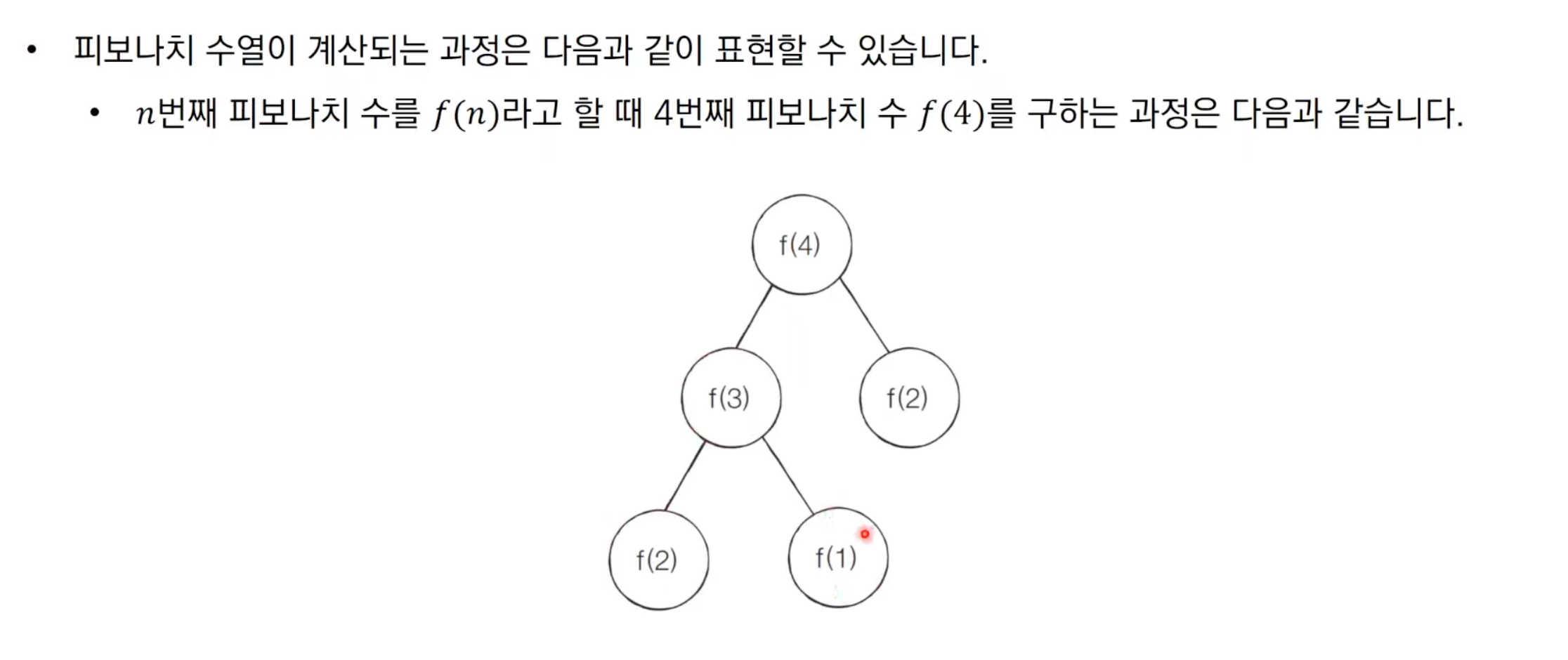
이미 구한걸 계속 더해나간다 디피가 딱 떠오르지 않는가 ?
그런데 우린 피보를 재귀로 보통 배운다 !
재귀의 문제를 한번 확인해보자
피보나치 수열 : 단순 재귀 코드
def fibo(x):
if x==1 or x==2:
return 1
return fibo(x-1)+fibo(x-2)
print(fibo(4))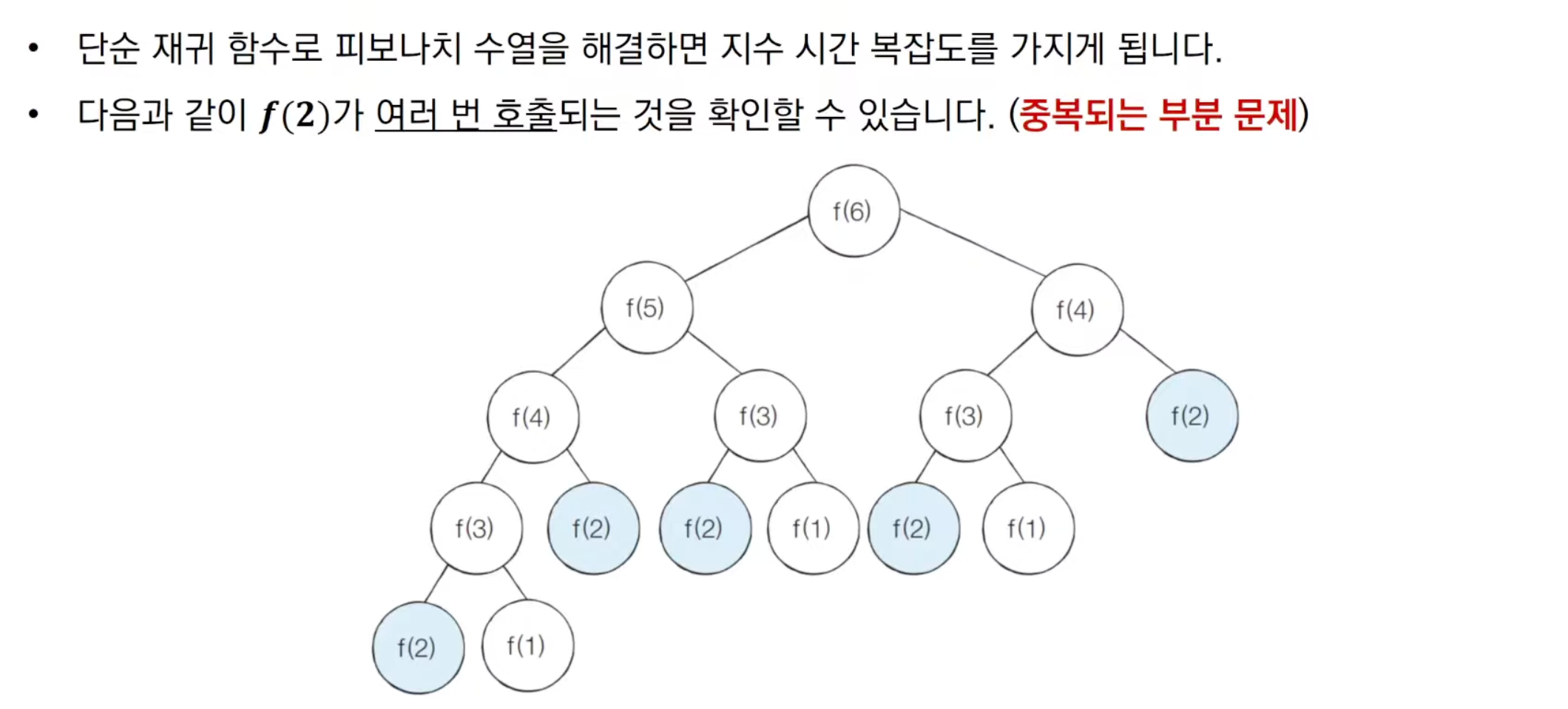
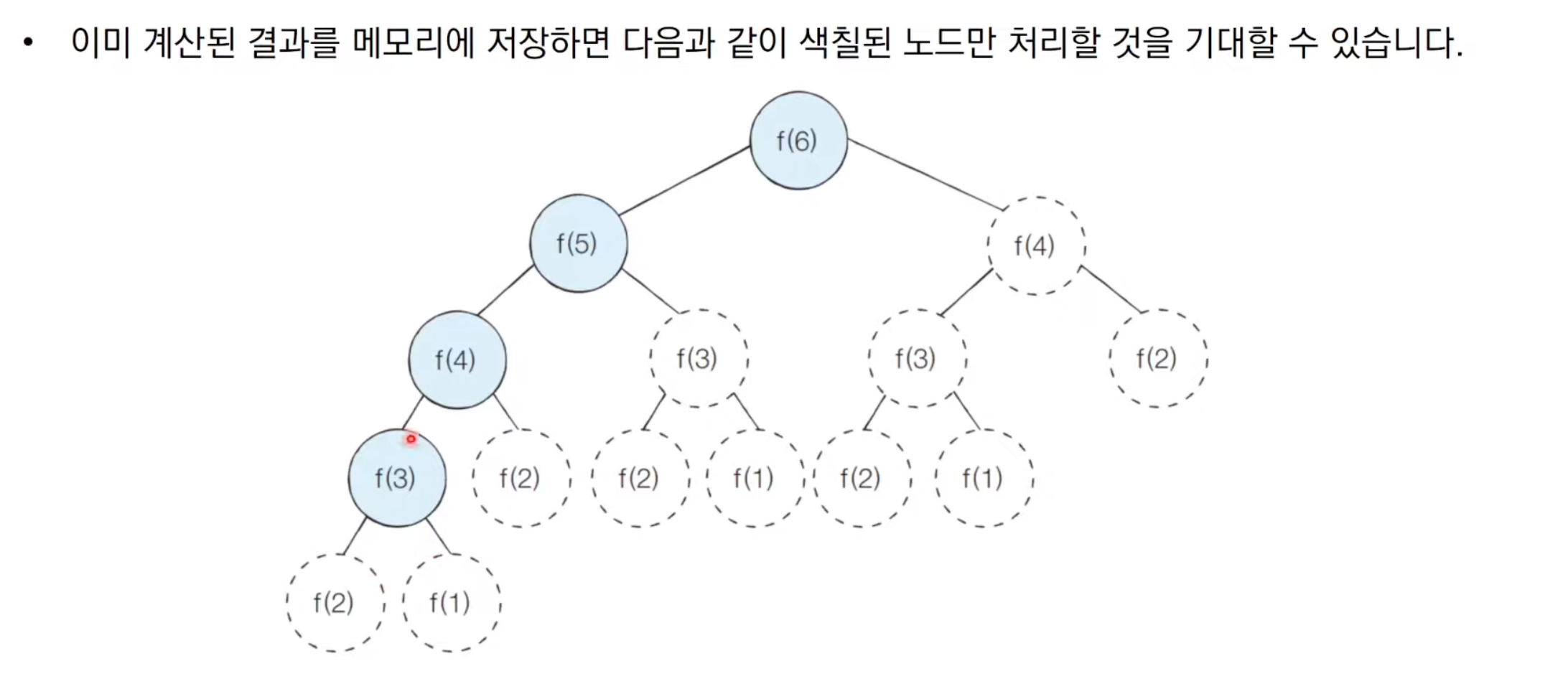
비효율적인 부분이 보이지 않는가!?
이미 해결해봤던 문제를 계속 중복적으로 구한다!
피보나치수열 재귀 : 시간 복잡도

엄~청 복잡하다
이제 앞서 말한 dp를 사용할 수 있는지 생각해보자

메모제이션(Memoization) : 하향식

탑다운 VS 보텀업

탑다운 : 재귀
보텀업 : 반복문 형식으로 구현한다.
dp를 접근할때 하향식 방법으로 접근할때 이미 구한걸가져오는 방식으로 메모리제이션을 사용하는것이다.
보통 보텀업을 많이쓴다
피보 : 탑다운
d = [0]*100
def fibo(x):
if x==1 or x==2:
return 1
if d[x] !=0:
return d[x]
d[x] = fibo(x-1) + fibo(x-2)
return d[x]
print(fibo(99))피보 : 보텀업
d = [0] * 100
d[1] = 1
d[2] = 1
n = 99
for i in range(3,n+1):
d[i] = d[i-1]+d[i-2]
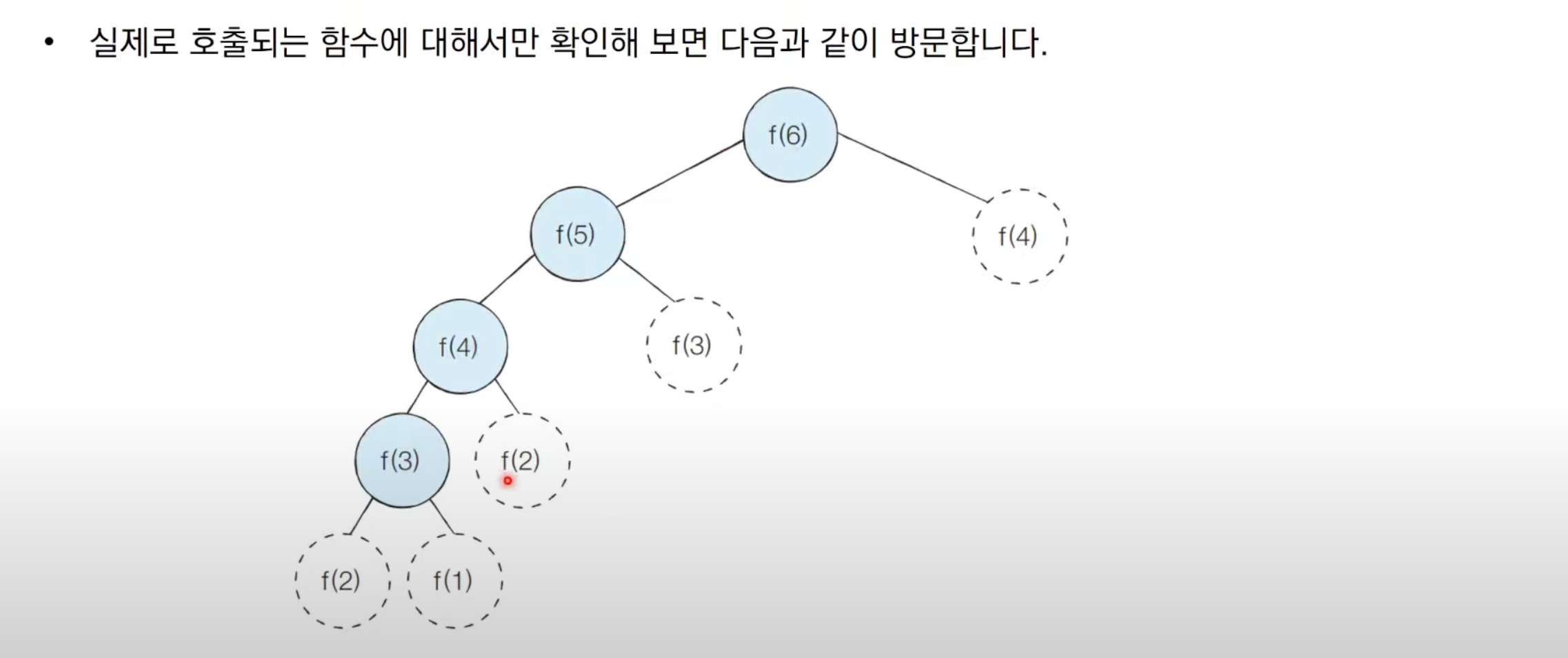
print(d[n])피보 : 메모이제이션 동작 분석
시간복잡도가 압도적으로 줄어든다
다이나믹 프로그램 vs 분할 정복

분할정복 예시
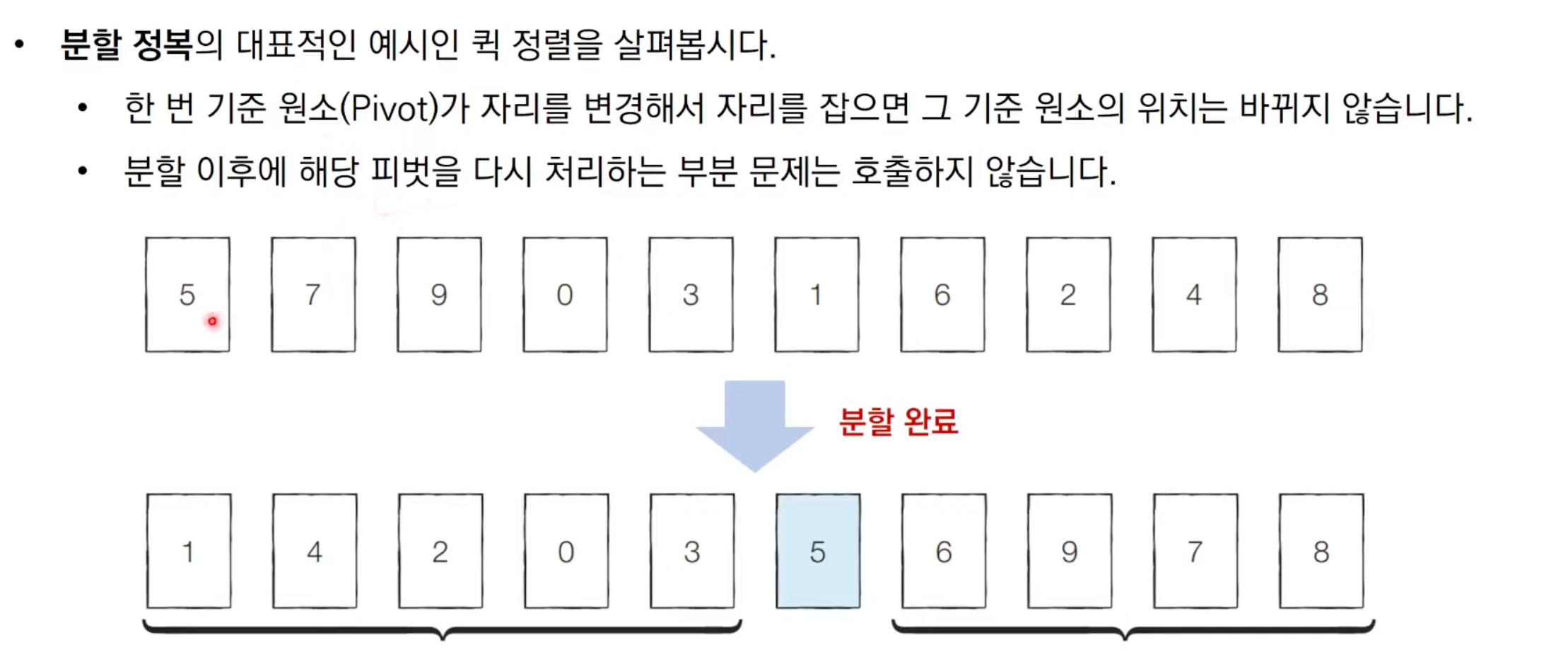
-> 피봇의 위치가 바뀌지 않음
-> 다른 부분문제에 포함되지 않음
다이나믹 프로그래밍 문제에 접근하는 방법

다이나믹 예제
개미전사
문제 설명

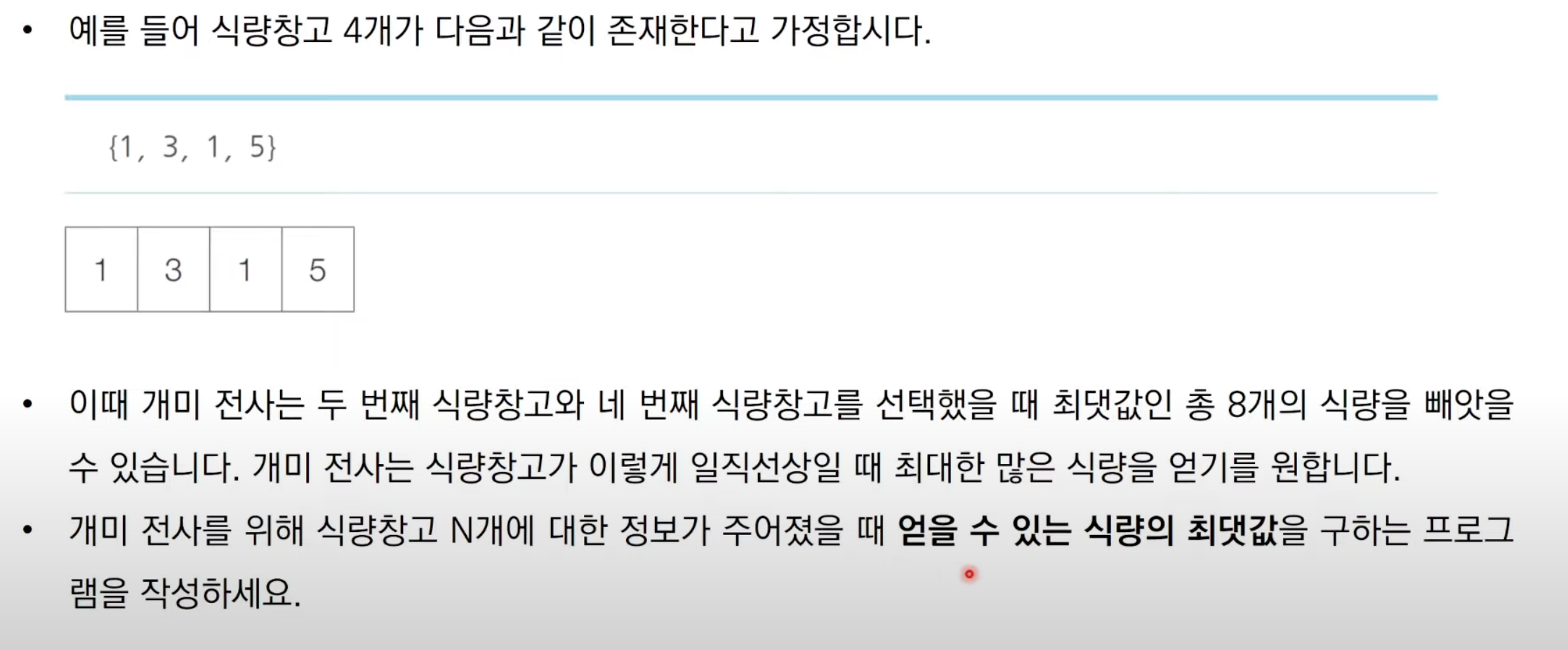

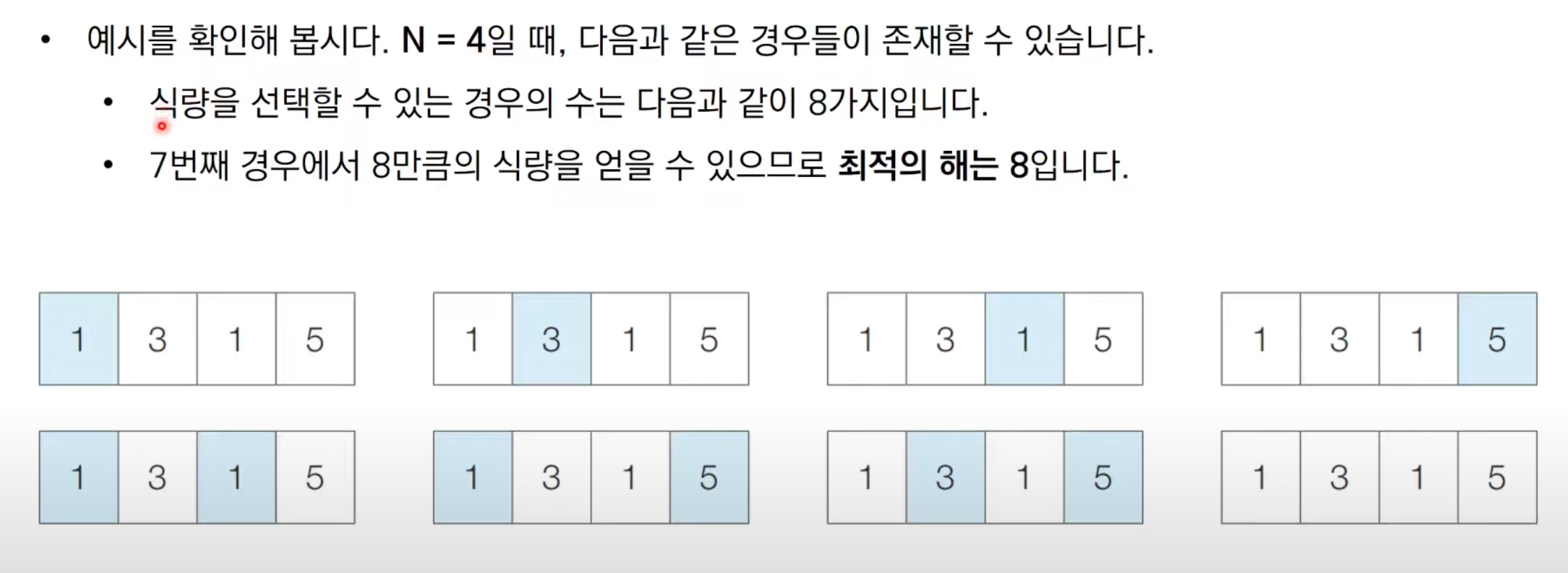
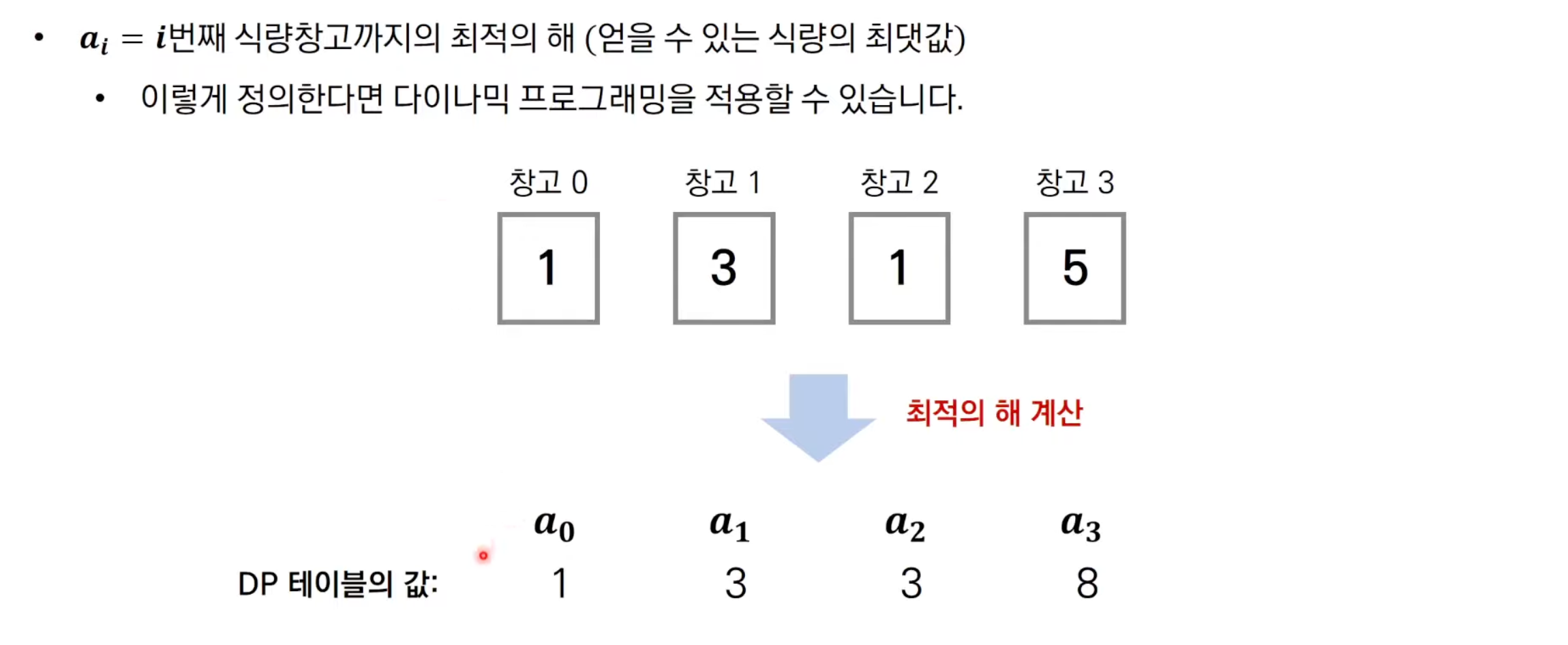
식량을 선택할 수 있는 경우의수를 모두 구한다
그 과정에서 이미 구했던것들을 "반복"해서 구하는 과정이 있을것이다
이 과정들을 보고 dp를 생각해내 풀어나가서 최대값을 찾아내면 될것이다.
해결아이디어
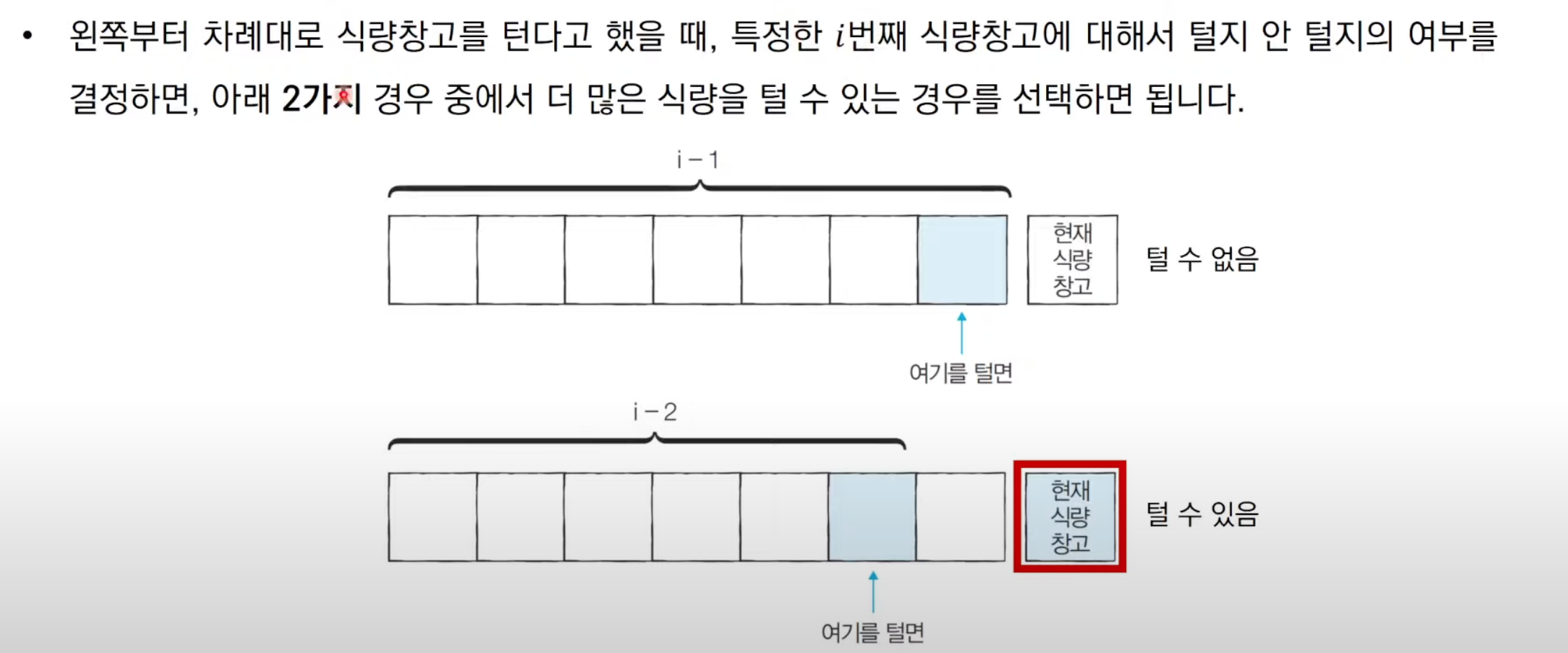

코드
n = int(input())
arr = list(map(int,input().split()))
d = [0]*100
d[0] = arr[0]
d[1] = max(arr[0],arr[1])
for i in range(2,n):
d[i] = max(d[i-1],d[i-2]+arr[i])
print(d[n-1])1로 만들기
문제 설명

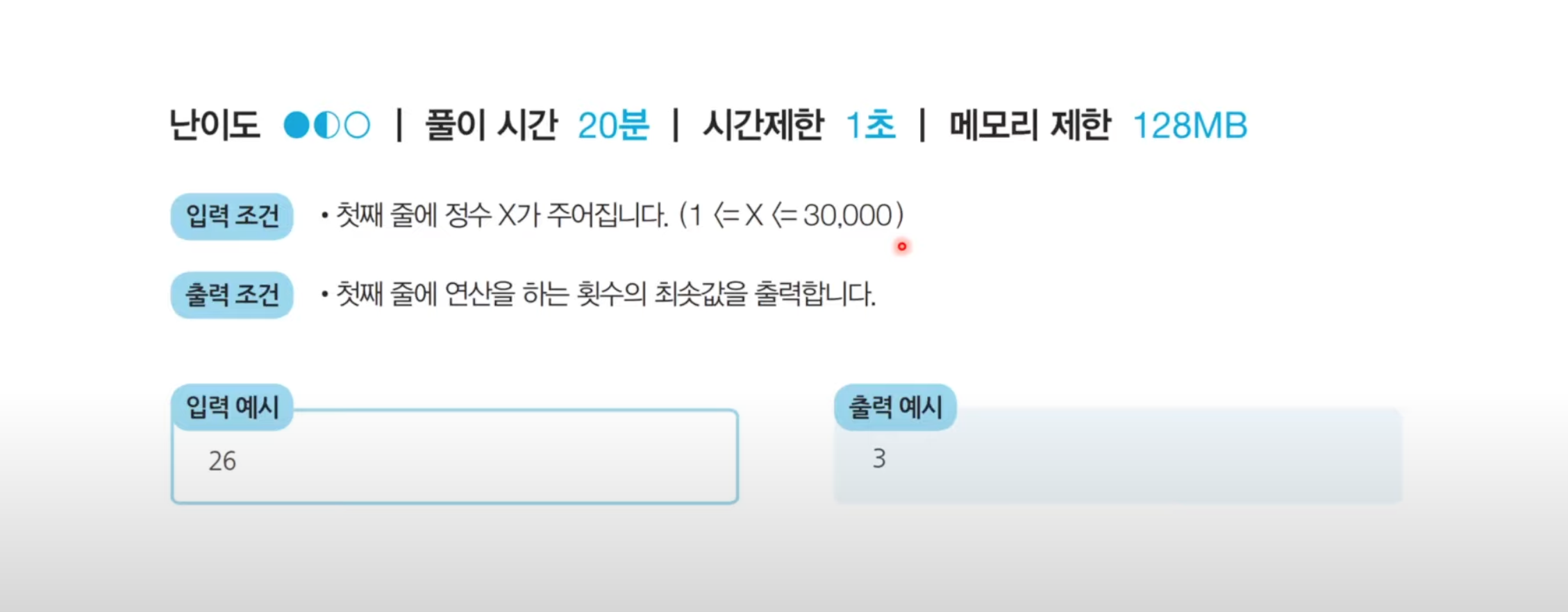
이 문제도 각케이스중 최소의 연산을 테이블에 저장하고 제일 최솟값을 출력하는 방식으로 가면될거같다.
문제 해결 아이디어
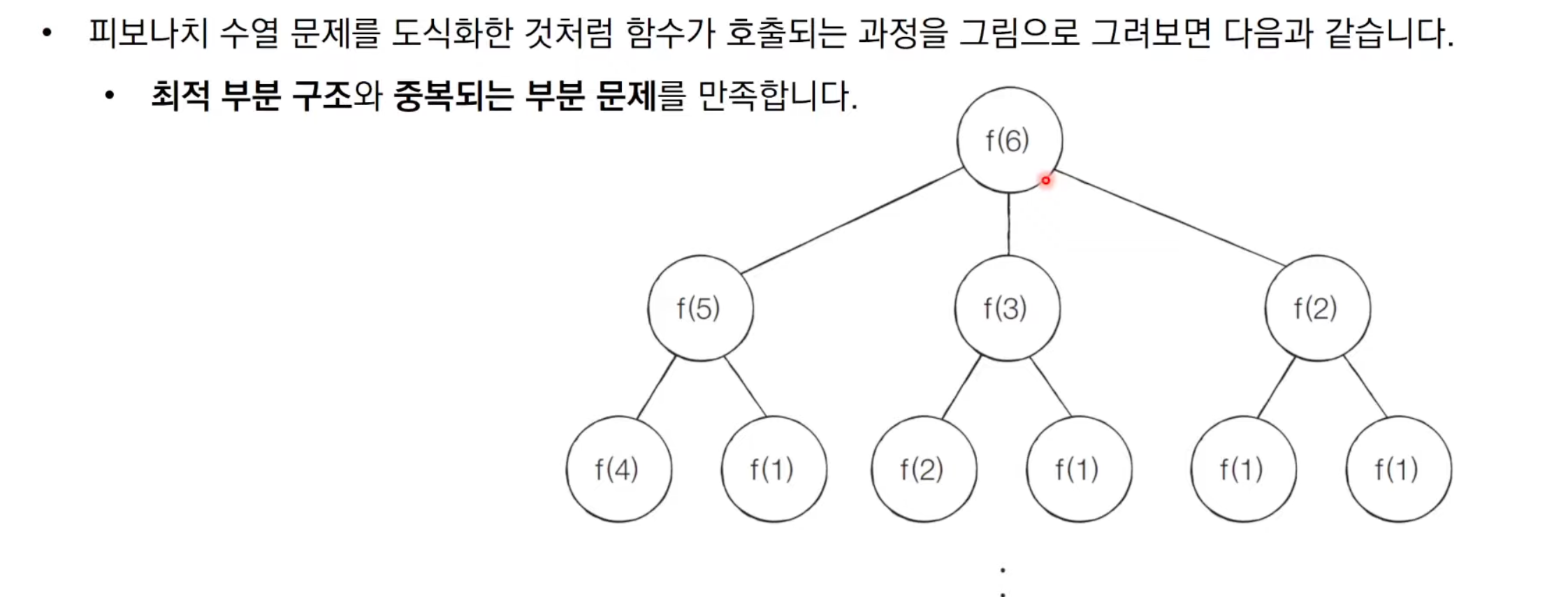
1이 될때까지의 문제와 차이점
1이 될때까지의 문제는 항상 나누는게 베스트임
이건 아님!!!

코드
x = int(input())
d=[0]*30001
for i in range(2,x+1):
d[i] = d[i-1]+1
if i%2==0:
d[i] = min(d[i],d[i//2]+1)
if i%3==0:
d[i] = min(d[i],d[i//3]+1)
if i%5==0:
d[i] = min(d[i],d[i//5]+1)
print(d[i])효율적인 화폐 구성

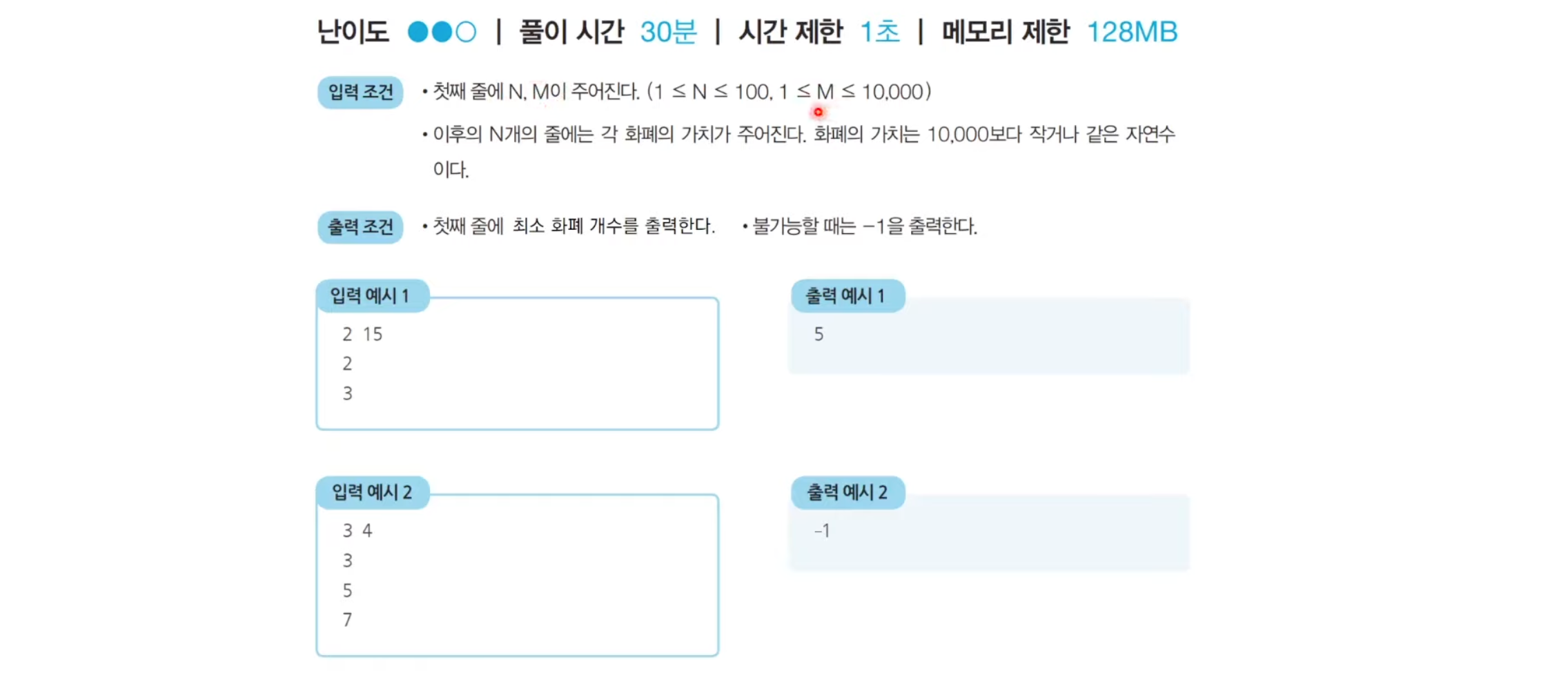
아마 1원부터 쭉쭉 그 돈을 만들기 위한 화폐의 개수를 구해나가서 사용하면 되는 문제일것같다
문제 해결 아이디어

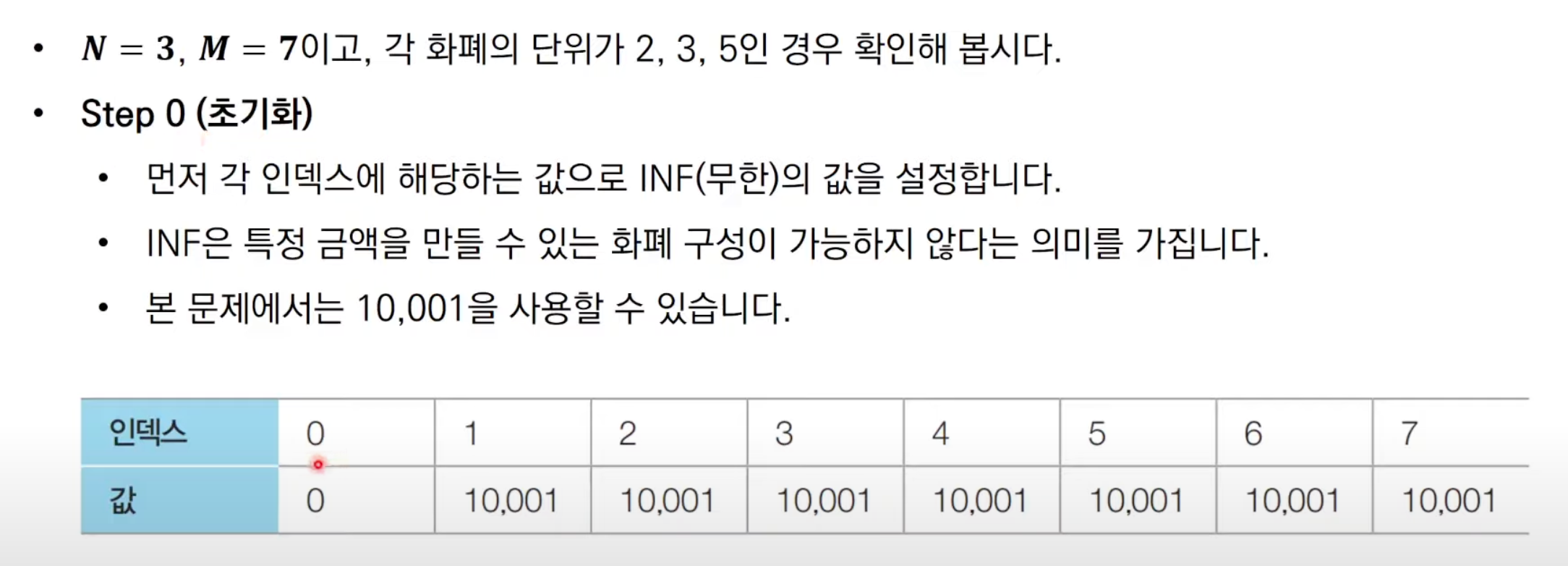
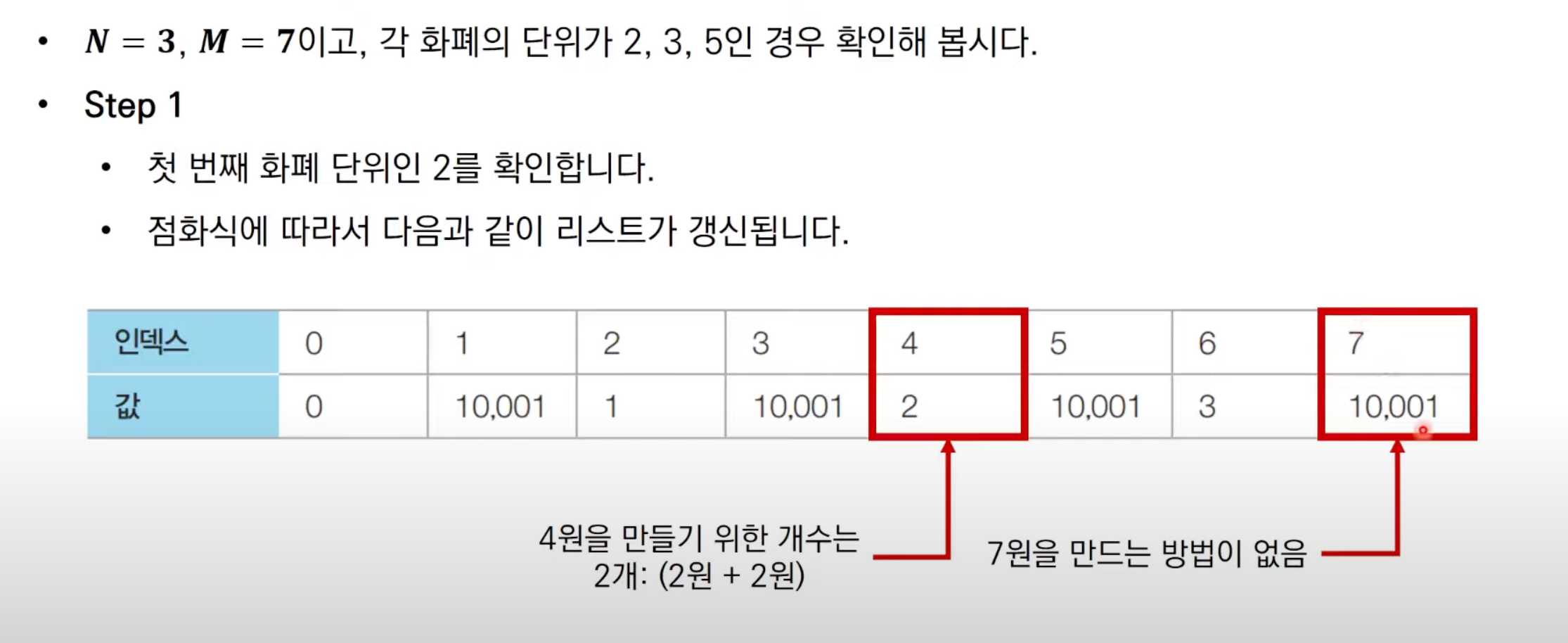
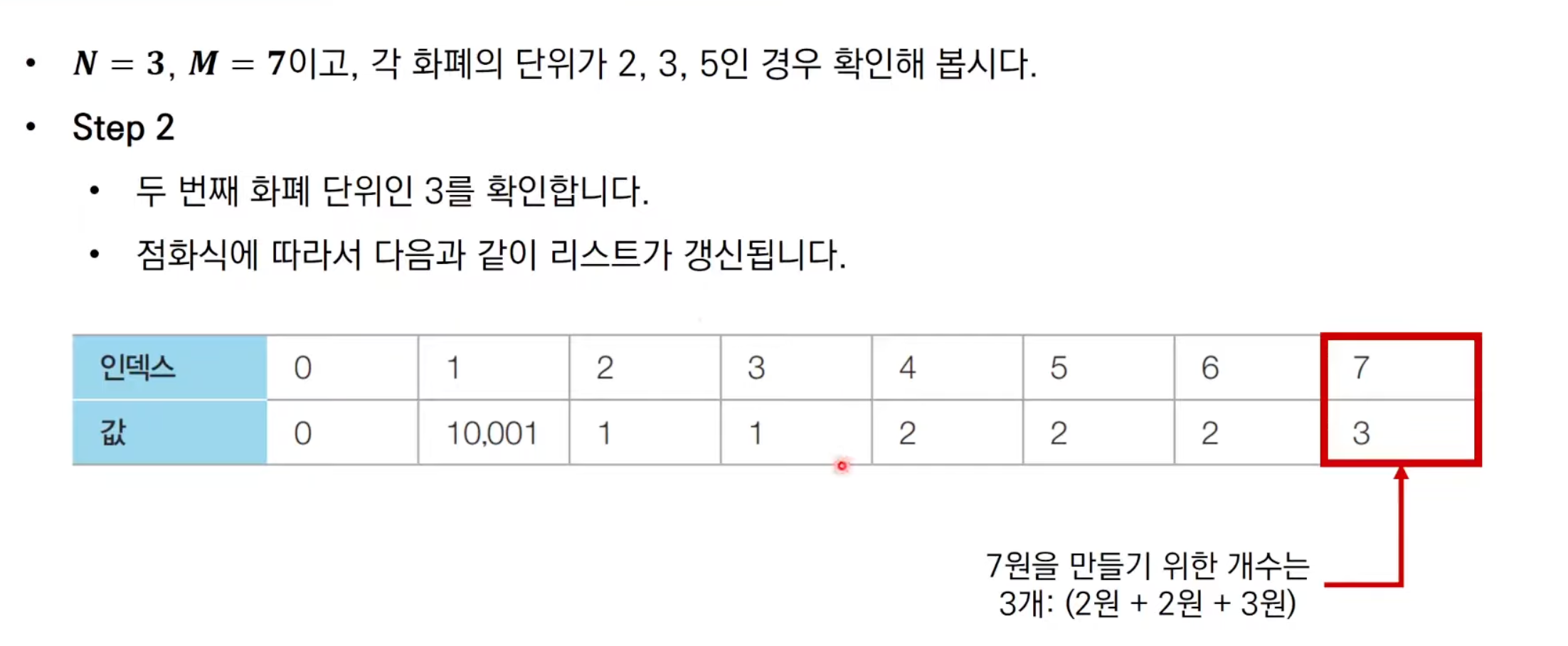
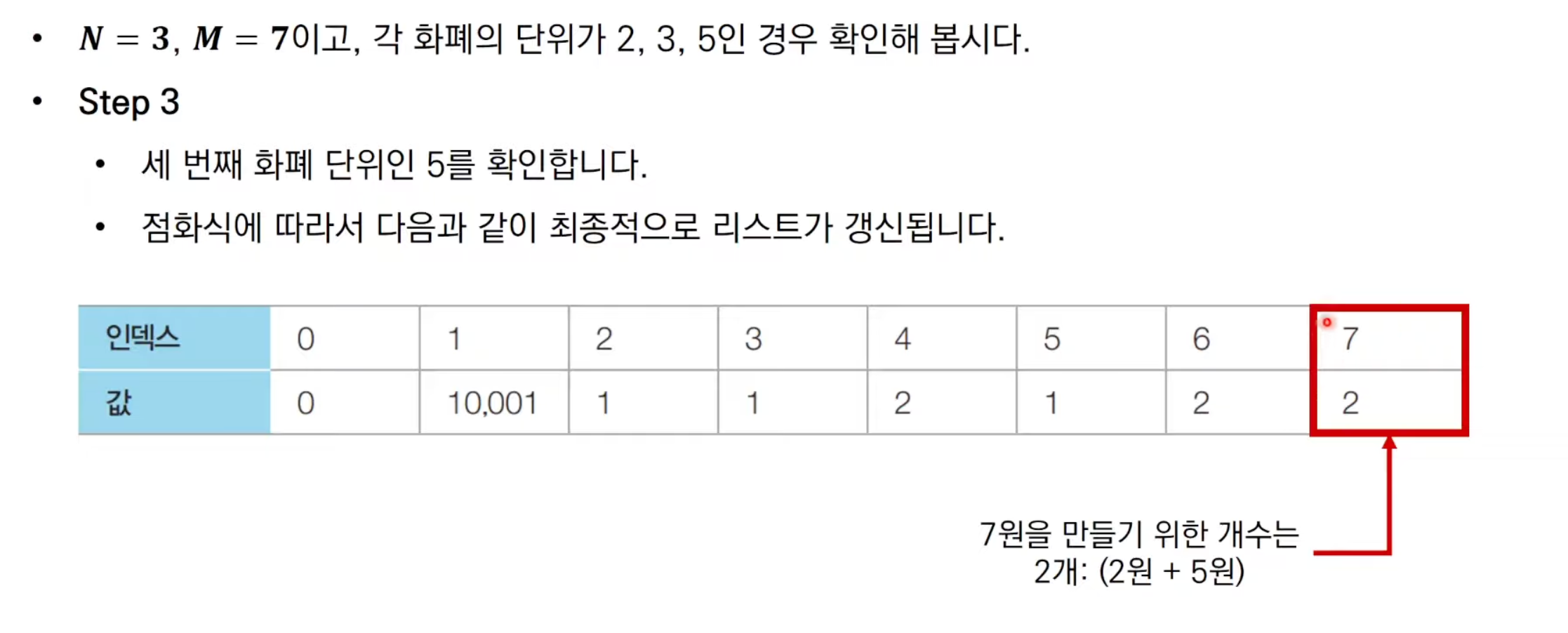
각각의 금액차례로 확인해보면 된다.
코드
n,m = map(int,input().split())
arr = []
for i in range(n):
arr.append(int(input()))
d = [10001] * (m+1)
d[0] = 0
for i in range(n):
for j in range(arr[i],m+1):
if d[j-arr[i]] != 10001 : #만들수있는 방법 존재
d[j] = min(d[j],d[j-arr[i]]+1)
if d[m]==10001:
print(-1)
else :
print(d[m])금광
문제 설명
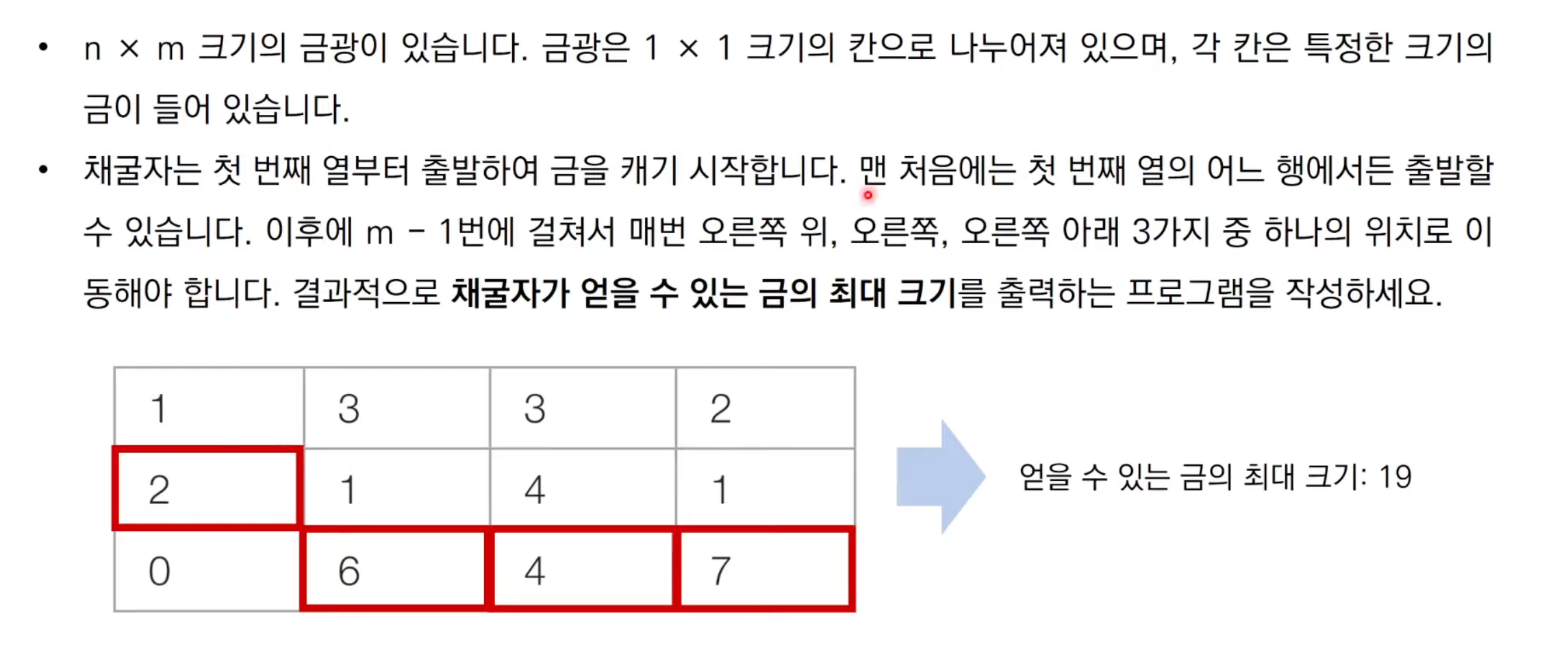

이 문제도 같은 방식으로
문제를 해결하면 될것같다
각 위치로 갈때마다 최댓값을 저장하는 방식 .. ?
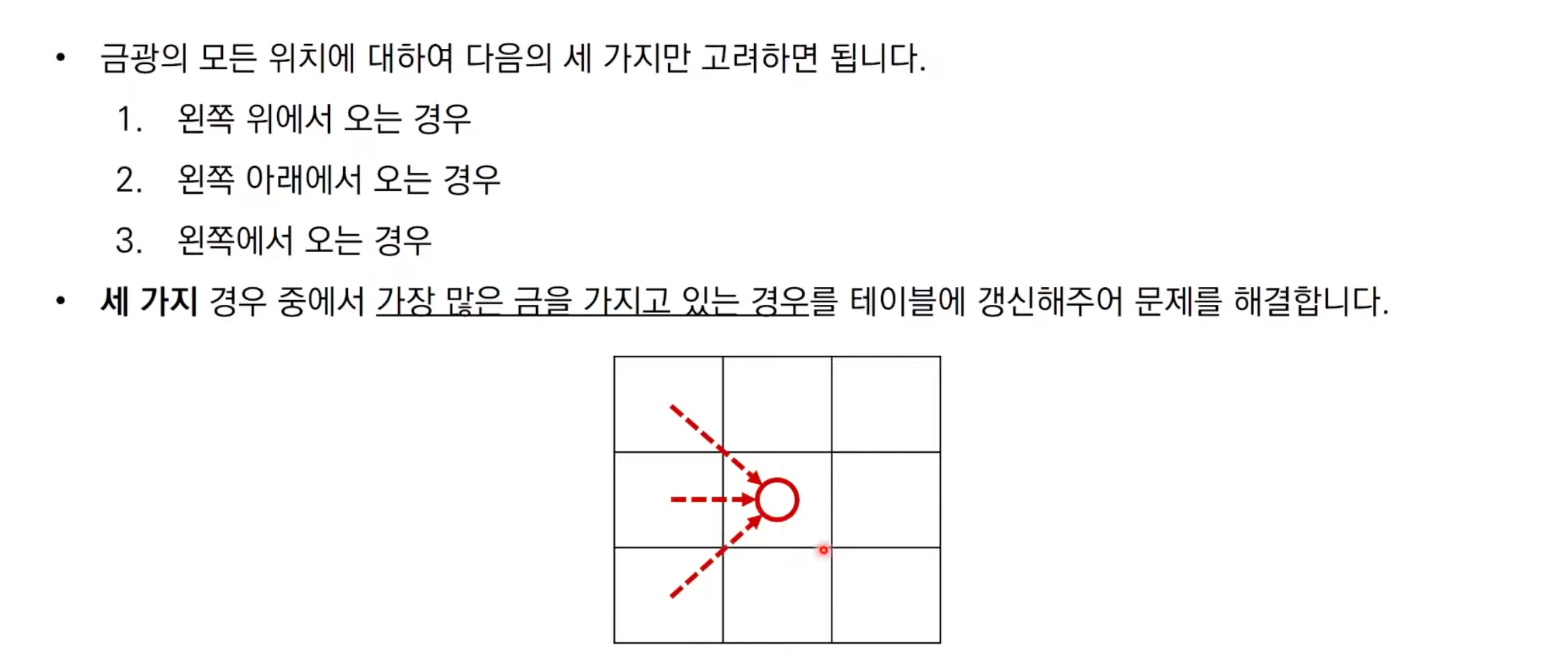
문제 해결 아이디어

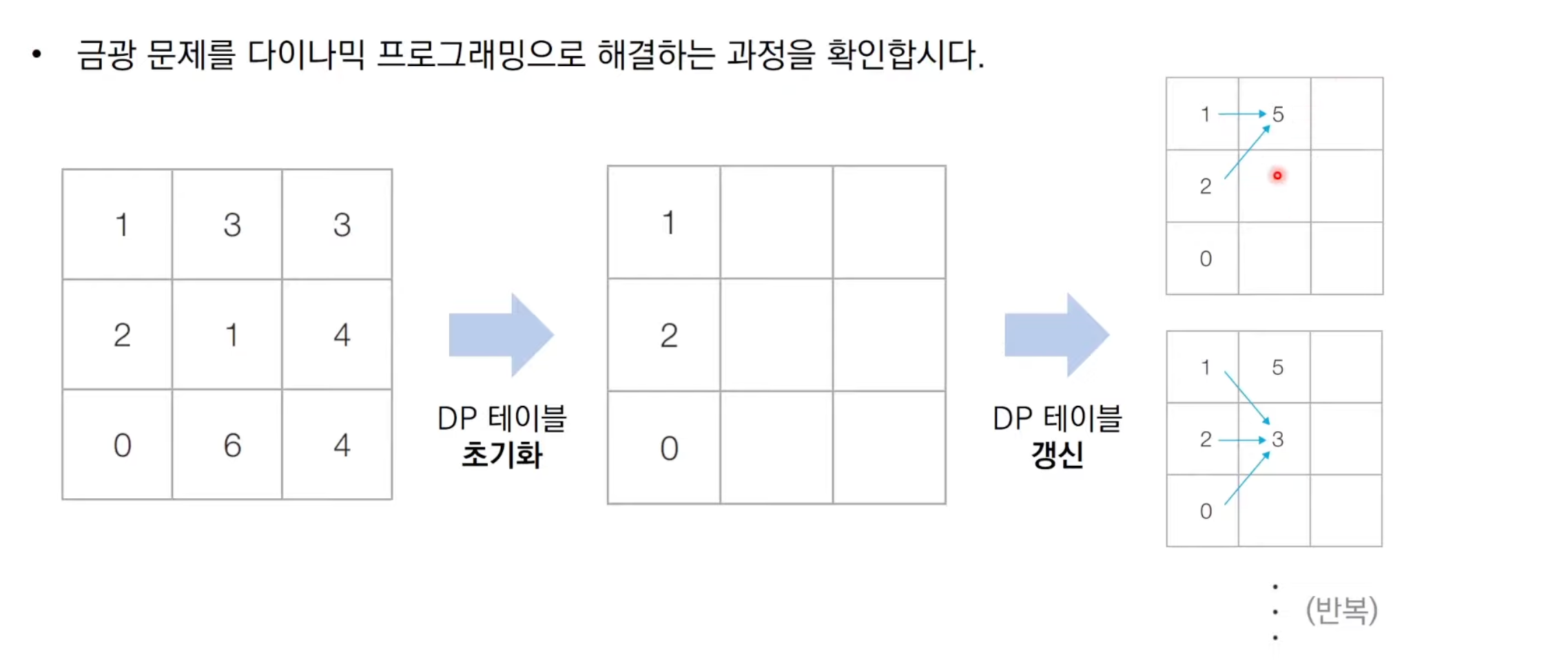
코드
for _ in range(int(input())):
n,m = map(int,input().split())
arr = list(map(int,input().split()))
dp = []
idx = 0
#2차원 dp테이블 초기화
for i in range(n):
dp.append(arr[idx:idx+m])
idx += m
for j in range(1,m):
for i in range(n):
if i==0:
left_up =0
else :
left_up = dp[i-1][j-1]
if i == n-1 :
left_down = 0
else :
left_down = dp[i+1][j-1]
left = dp[i][j-1]
dp[i][j] = dp[i][j] + max(left_up,left_down,left)
result = 0
for i in range(n):
result = max(result,dp[i][m-1])
print(result)병사 배치하기
문제 설명

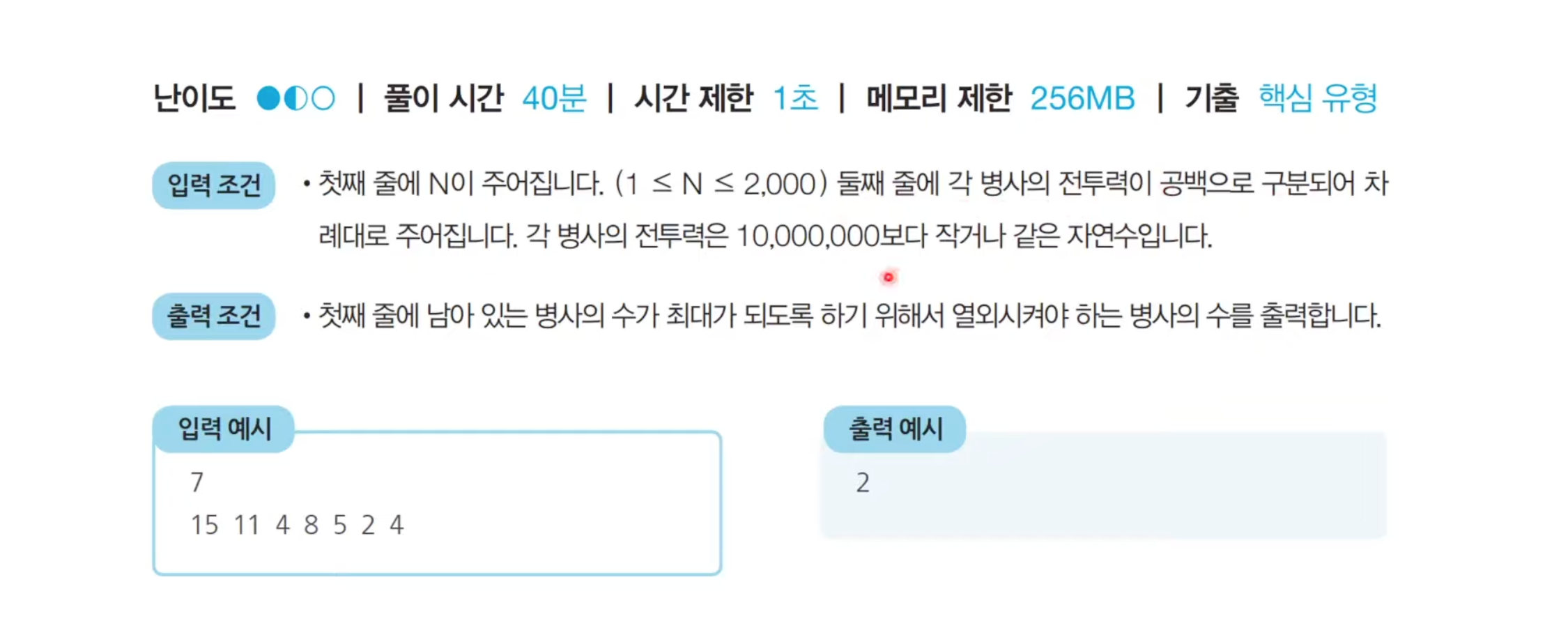
문제 해결 아이디어


문자열 길이를 세주는것이다.. !
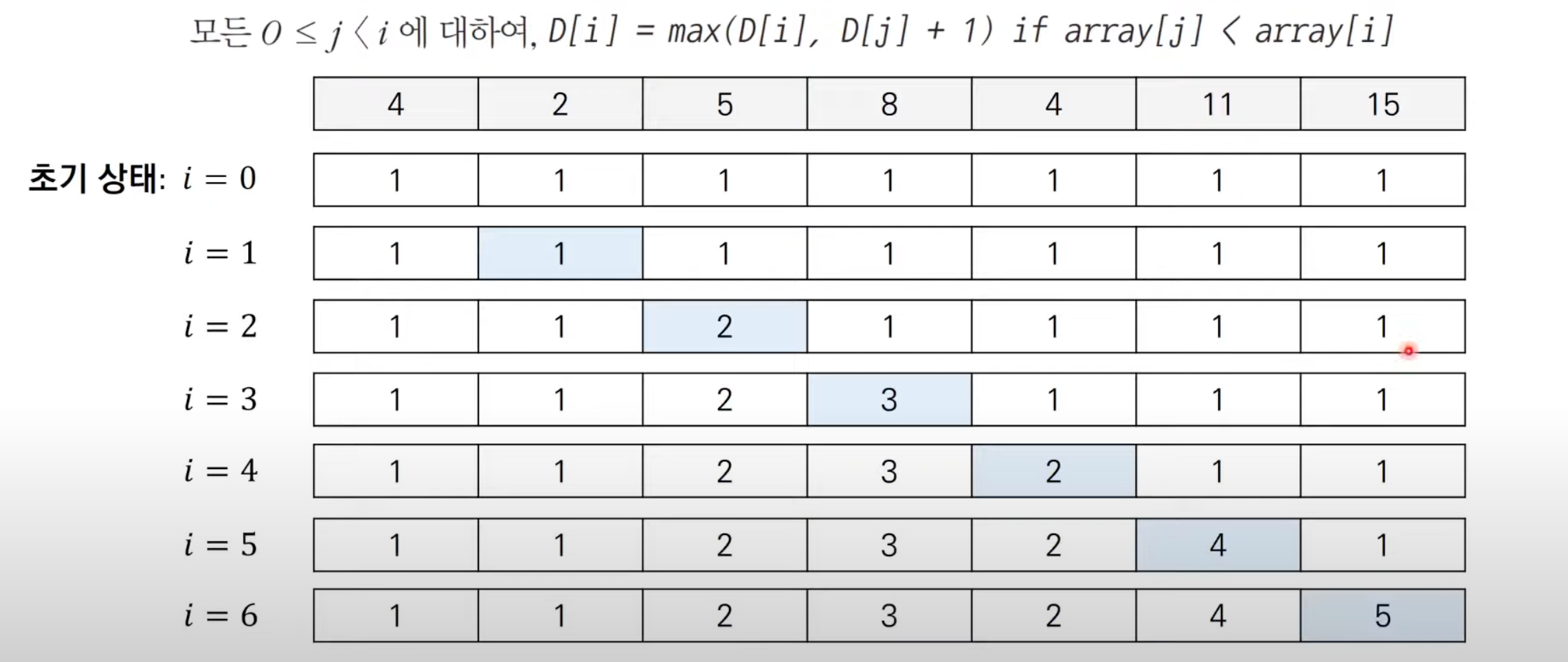

코드
n = int(input())
arr = list(map(int,input().split()))
arr.reverse()
dp = [1]*n
#LIS 알고리즘 수행
for i in range(1,n):
for j in range(0,i):
if arr[j]<arr[i]:
dp[i] = max(dp[i],dp[j]+1)
print(n-max(dp))DP는 증말.... 미지의세계이다
결국 점화식을 잘작성할줄 알고 이를 토대로 코드를 잘작성해야 하는 유형인것같다 ...