[이코테]최단 경로 알고리즘 - 플로이드 워셜 알고리즘

플로이드 워셜 알고리즘

그놈의 디피...
시간복잡도가 log(n**3)으로 디따크다..
앞서 알아봤던 다익스트라에 비하면 진짜..
근데 구현난이도가 쉬워서 n이작을때 사용하면된다.

플로이드 워셜 알고리즘 : 동작 과정 살펴보기

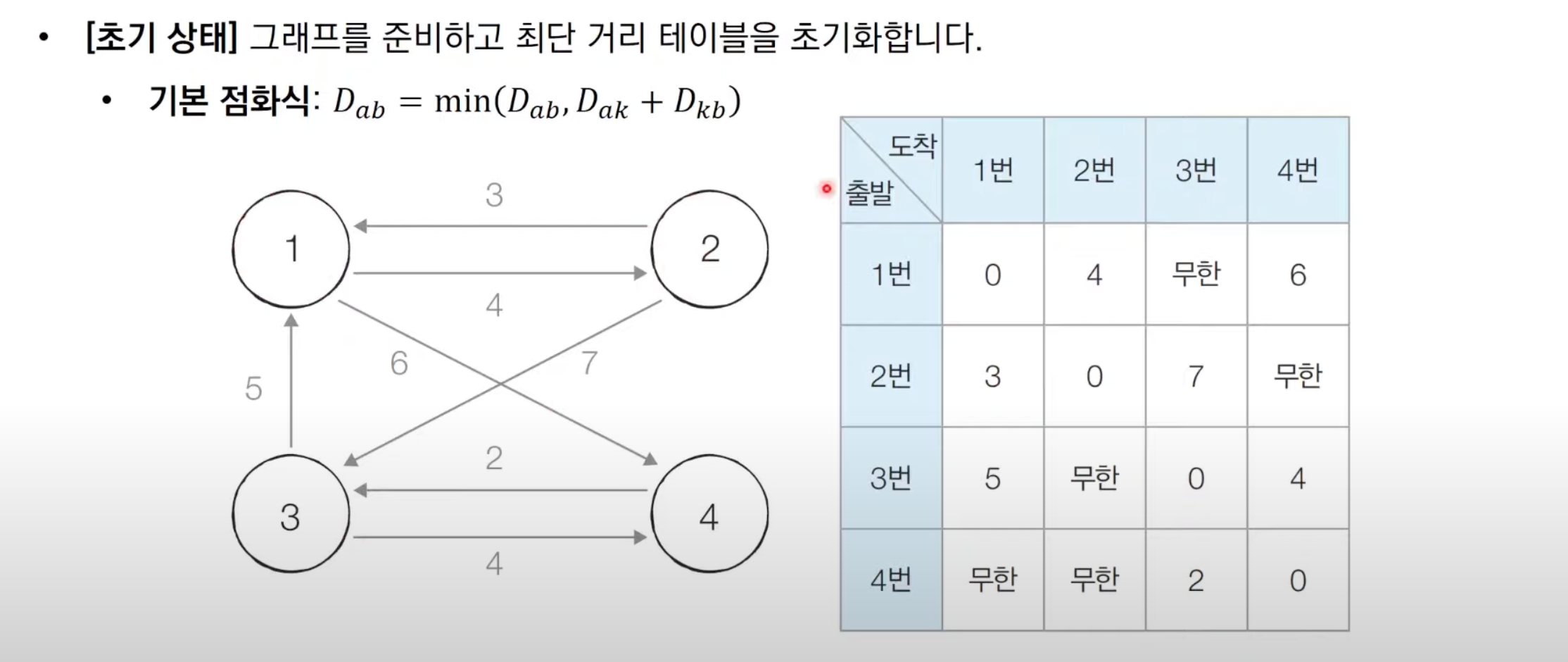
킹갓..제네럴 삼중반복문을 통해서 이를 구현할 수 있다.

플로이드 워셜 알고리즘 : 구현

INF = int(1e9) 

# 노드의 개수 및 간선의 개수 입력받기
n = int(input())
m = int(input())
# 2차원 리스트를 만들고, 무한으로 초기화 
graph =[[INF] * (n+1) for _ in range(n+1)]

# 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화 
for a in range(1,n+1):
    for b in range(1,n+1):
        if a == b:
            graph[a][b] = 0 

# 각 간선에 대한 정보를 입력 받음 
for _ in range(m):
    #A->B 비용 C 
    a,b,c = map(int,input().split())
    graph[a][b] = c 

# 점화식에 따라 폴로이드 워셜 알고리즘 수행 
for k in range(1,n+1):
    for a in range(1,n+1):
        for b in range(1,n+1):
            graph[a][b] = min(graph[a][b],graph[a][k]+graph[k][b])

# 수행된 결과를 출력 
for a in range(1,n+1):
    for b in range(1,n+1):
        #도달할 수 없는 경우 무한 
        if graph[a][b] == INF:
            print("INF",end=" ")
        else :
            print(graph[a][b],end=" ")
    print()

플로이드 워셜 알고리즘 성능 분석

쿠쿠,,, 시간복잡도 오진당