[자료구조] 정렬(Sorting) 10-1(선택 정렬)

선택 정렬 : 이해와 구현

이번에 소개하는 선택정렬은 버블 정렬보다도 쉽고 간단한 알고리즘이다.

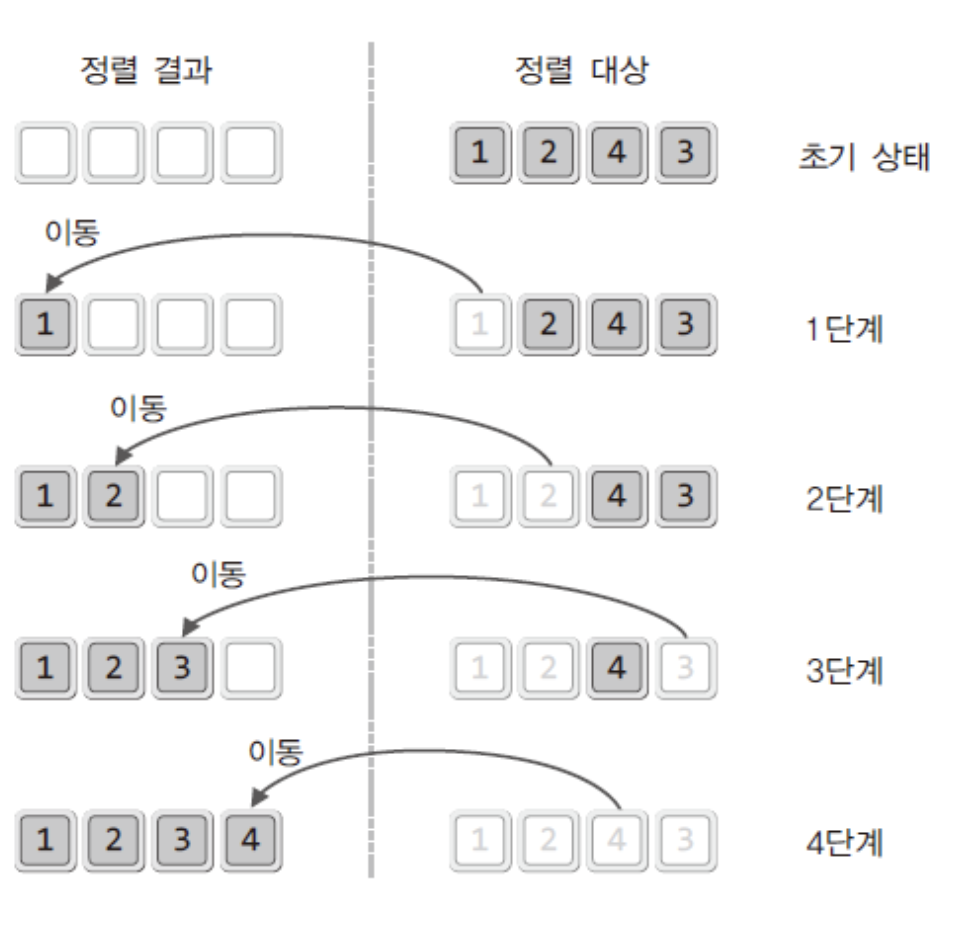
그림만 봐도 이해가 되지 않는가!?
말 그대로 선택해서 정렬한다!
그런데.. 보면 이런 생각이 들것이다

"그럼 선택 정렬은 정렬결과를 담을 별도의 메모리 공간이 필요하겠네요!"

위 그림 대로 진행한다면 그렇지만 !
알고리즘을 개선 시키면 필요없다!

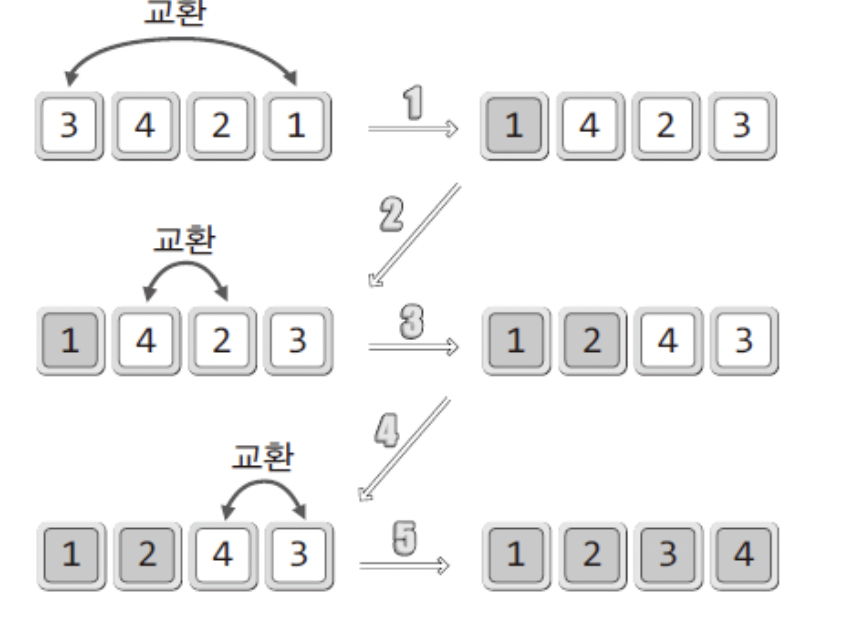
교환이라기 보다는 다음과 같이 이해해야한다.

정렬 순서상 가장 앞서는 것을 선택해서 가장 왼쪽으로 이동시키고, 원래 그 자리에 있던 데이터는 빈자리에 가져다 놓는다.

결론적으로 교환은 맞긴 맞지만!
"빈 자리를 활용하는 과정에서 비롯된 교환" 이라는 사실을 이해해야한다.

그럼 이제 예를 보이겠다!

#include <stdio.h>

void SelSort(int arr[],int n)
{
    int i,j;
    int maxIdx;
    int temp;
    
    for(i=0;i<n-1;i++)
    {
        maxIdx = i;
        
        for(j=i+1 ; j<n ; j++) //최솟값 탐색
        {
            if(arr[j]<arr[maxIdx])
            {
                maxIdx = j;
            }
        }
        //change
        temp = arr[i];
        arr[i] = arr[maxIdx];
        arr[maxIdx] = temp;
    }
}

int main(void)
{
    int arr[4] = {3,4,2,1};
    int i;
    
    SelSort(arr, sizeof(arr)/sizeof(int));
    
    for(i=0;i<4;i++)
    printf("%d ", arr[i]);
    
    printf("\n");
    return 0;
}

선택 정렬 : 성능 평가

코드만 봐도 버블 정렬과 성능상 큰 차이가 없음을 추리할 수 있다.
비교연산 횟수의 확인을 위해 반복문을 보자 !
그런데..
얘도..

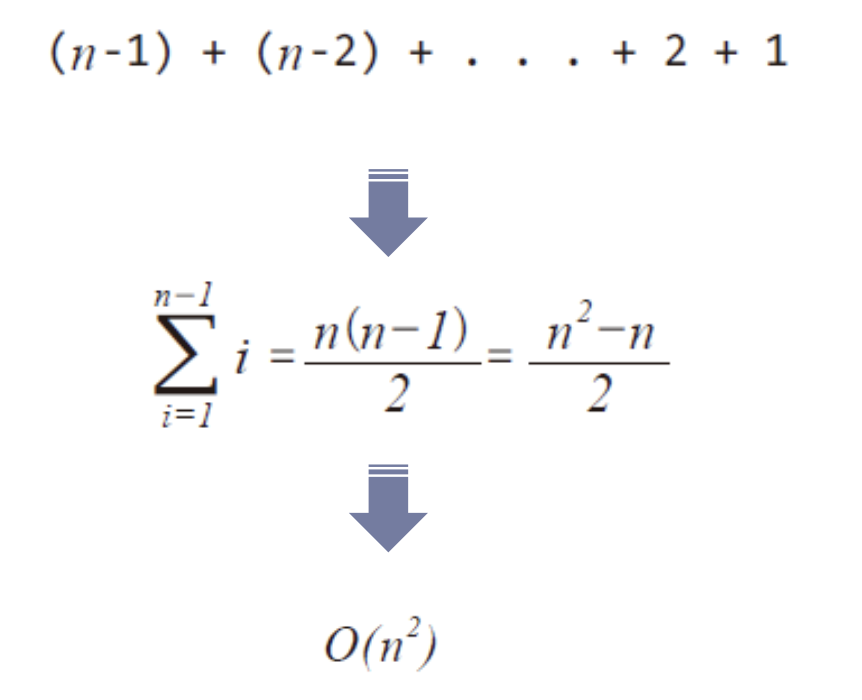
빅-오가 버블 정렬과 동일히다.
그렇다면 이동횟수도 버블 정렬과 차이가 없을까!?
그러나!!!!
여기에는 제법 차이가 있다.
버블 정렬이나 선택정렬이나 데이터의 교환을 위해 세 번의 대입연산이 다음과 같이 진행된다.

temp =A;
A = B;
B = temp;

하지만! 다르다!
눈치챘는가!
바로 존재하는 위치가 다르다.

버블 정렬의 경우에는 안쪽 for문에 속해있고
반면 선택 정렬의 경우 바깥쪽 for문에 속해있다.
따라서 선택 정렬의 경우 n-1회의 교환이 이뤄지므로 데이터의 이동횟수는 이의 세 배인 3(n-1)dlek.

그러므로 이동연산에 대한 빅-오는 최선이나 최악이나 O(n)이다.

버블 같은 경우 최선일경우 0이고 데이터들이 늘 최악의 상황으로 배치되지 않는다는 점을 감안하면.. 이 둘의 우열을 가리는 것은 무의미 하다 !