윤성우의 열혈 자료구조
1.[자료구조]큐(Queue)[7-1]
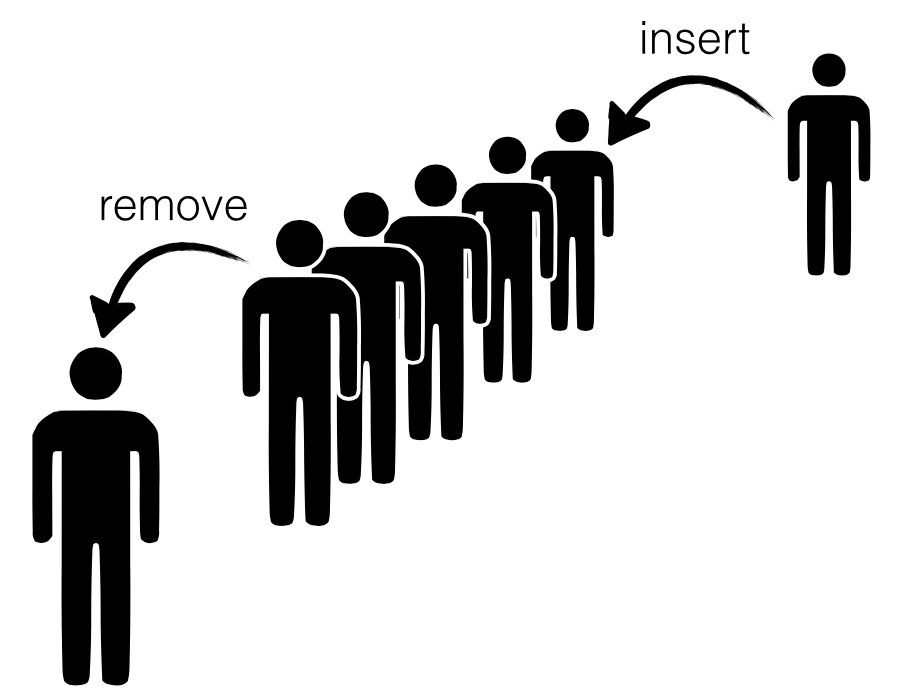
스택과 큐의 차이 스택은 먼저 넣은것을 마지막에 빼는 선입후출
2.[자료구조] 큐(Queue)(7-2) 큐의 배열 기반 구현
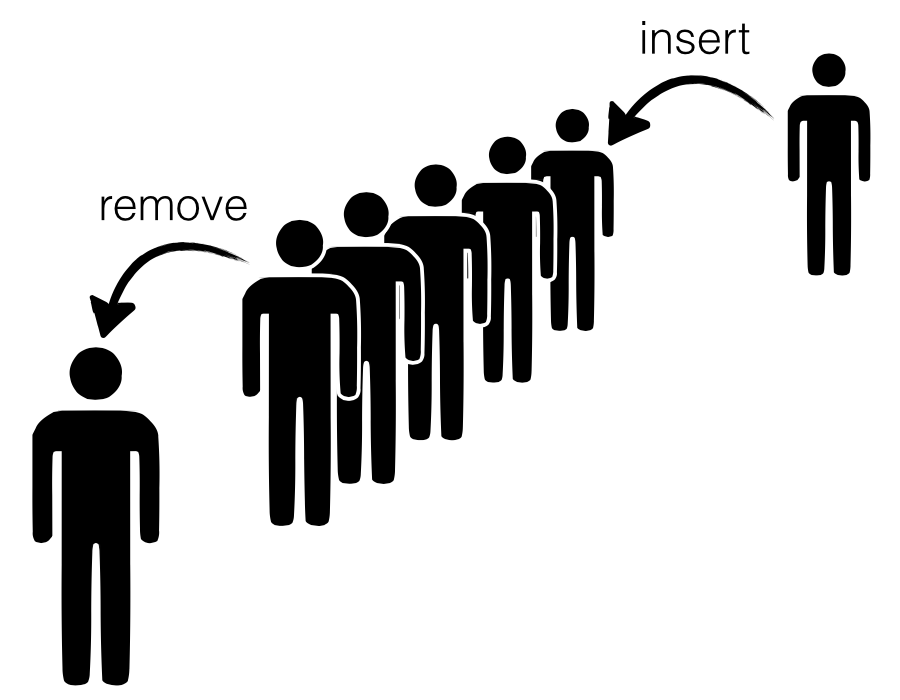
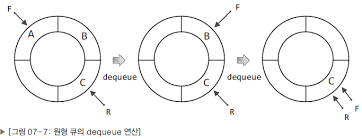
큐의 머리를 F 꼬리를 R이라고 생각하자 ! enqueue(데이터추가)연산 시 F는 그대로 있는 채 꼬리인 R이 한칸씩 뒤로가리키면서 연산이 진행된다. 그렇다면 ! dequeue연산시에는 이와는 반대로 F를 참조하여 머리를 삭제해 나가는 방식이다 에는 일반적이지 않은
3.[자료구조]원형 큐(Circular Queue) - 개선
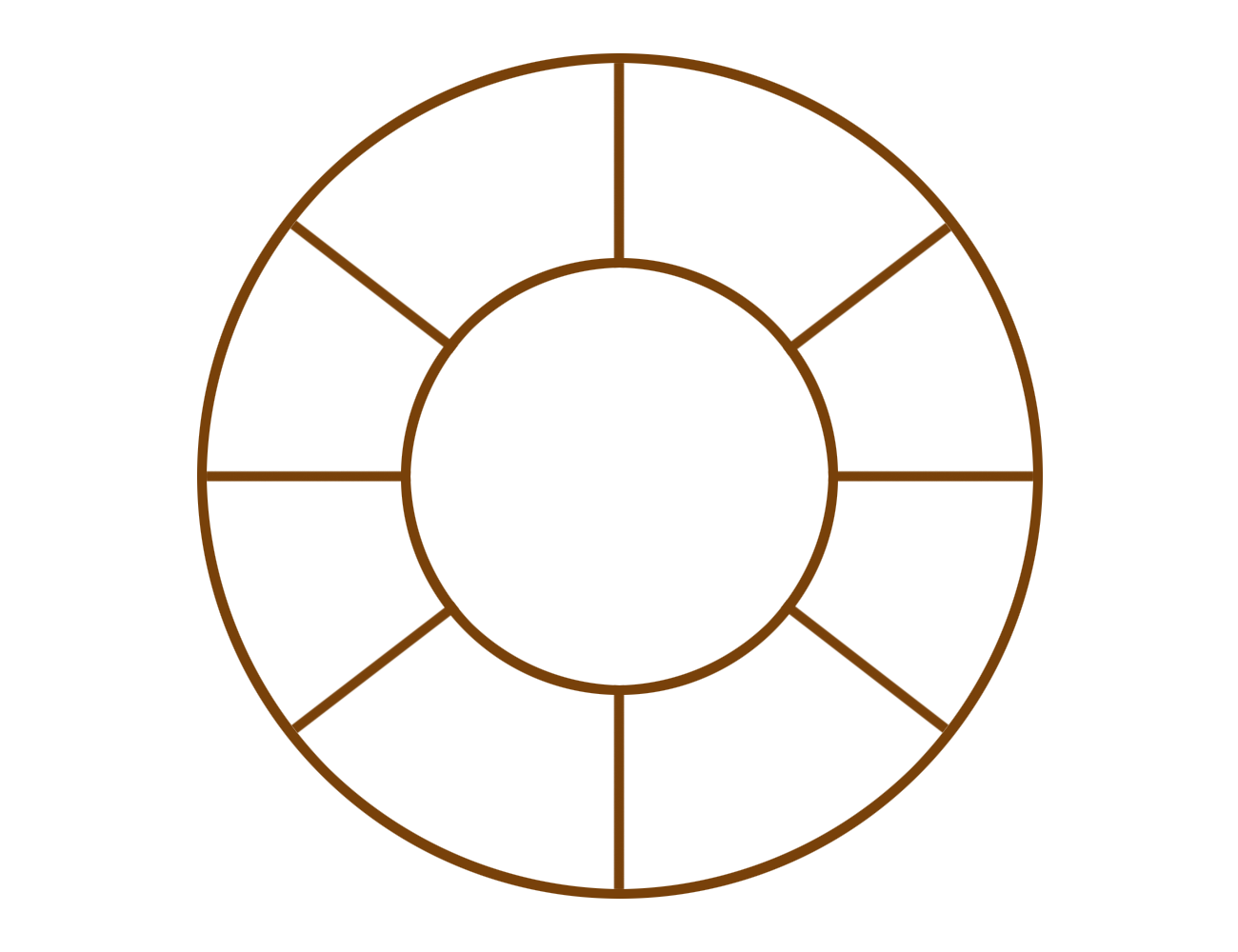
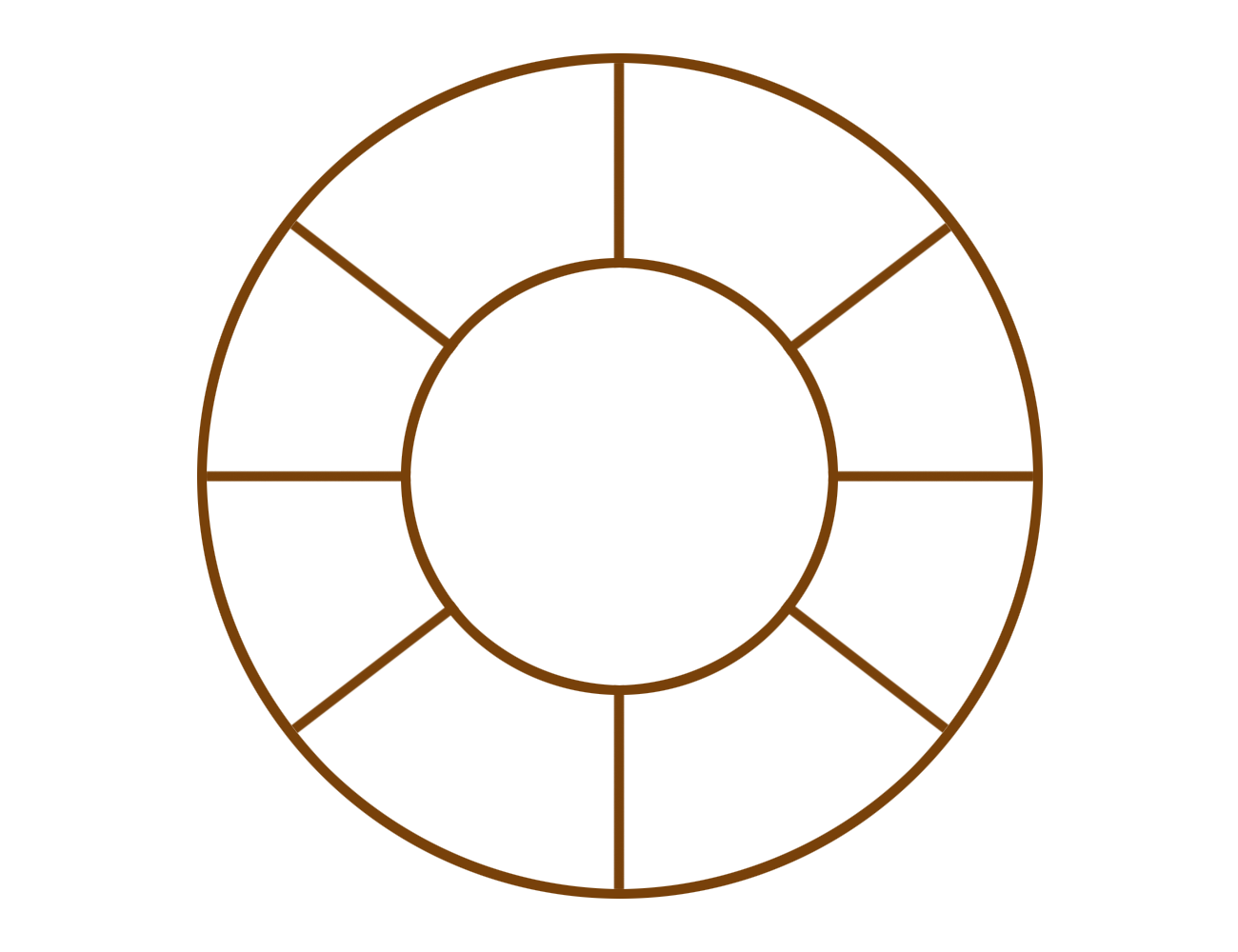
그림을...그렸는데.... 오류때문에 열리지않아,,text로 임시로 씁니다...원형 큐를 활용하여 앞선 큐의 단점을 보완할 수 있는데원형 큐에서도 생각할것이 하나 더 있다.그것은 바로 큐가 완전 비어져있을때와 꽉 차 있을때 R 다음 F인 같은 형식을 띠고 있어서 차이점
4.[자료구조]개선된 원형 큐의 구현
배열기반의 큐는 대부분 원형 큐를 의미한다고 봐도 무리가 아니다.코드는 그저 F와 R이 배열의 끝에 도달했을 떄 앞으로 이동 시키는 것이 전부이다. CircularQueue.h 헤더 파일을 통해서 함수들을 정의해주었다. CircularQueue.c이 중 nextPosI
5.[자료구조]큐의 연결리스트 기반 구현
연결리스트 기반으로 구현한다고 쳐도 여전히 스택과 큐는 차이점이 있는데 바로 stack은 push/pop이 이뤄지는 위치가 동일한 반면, 큐는 enqueue/dequeue가 이뤄지는 위치가 다르다는것이다. 우선 연결리스트 기반 큐의 헤더파일을 소개한다 ! ListBas
6.[자료구조]큐의 활용
큐는 운영체제 및 네트워크 관련된 소프트웨어의 구현에 있어서 중요한 역할을 하는 자료구조이다 !큐잉 이론 이라는 학문에서는 수학적으로 모델링 된 결과의 확인을 위해서 특정 현상을 시뮬레이션 하게 되는데 여기서 큐가 중요한 역할을 담당한다. 따라서 ! 우리도 시뮬레이션이
7.[자료구조]덱(Deque)의 이해와 구현
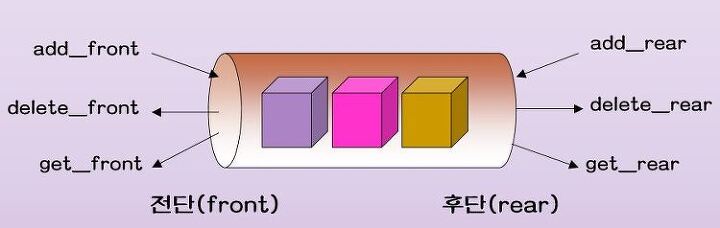
이다면 double-ended queue 의 줄임말이다.따라서 덱의 ADT를 구성하는 핵심 함수 네 가지의 기능은 ! 앞으로 넣기뒤로 넣기앞에서 빼기뒤에서 빼기 이다.이를 통해 덱의 ADT를 정의하자면 ...! 덱 또한 연결리스트/배열로 구현 가능하지만 베스트는 양방향
8.[자료구조]문제 7-1[덱을 기반으로 큐를 구현하기]
덱을 큐처럼 사용 할 수 있으니 덱을 이용해서 큐를 구현할 수 있다!!구현해봐라 !DequeBaseQueue.hDequeBaseQueue.c생각외로 간단하지 않는가..?그 이유는 앞에서 삽입/빼기 뒤에서 삽입/빼기 가 가능한 이미 만들어진 덱의 함수에서 큐를 구현한다는
9.[자료구조] Tree (8-1)
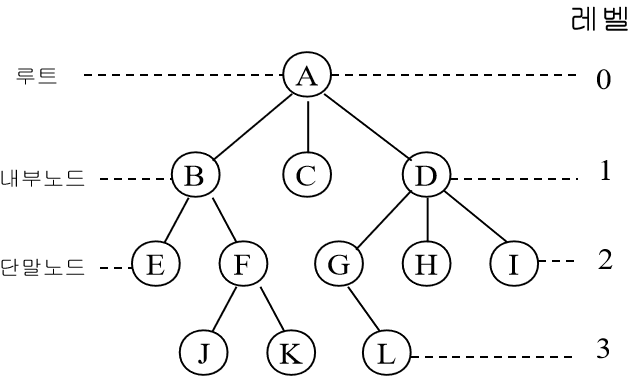
트리를 통해서 무엇인가를 저장한다는 생각보다 "표현" 한다고 생각하는 것이 좋다."데이터의 저장, 검색 및 삭제가 용의하게 정의 되어있나여?"보다는"트리의 구조로 이뤄진 무엇인가를 표현하기에 적절히 정의되어 있나요?" 라는 시야가 필요하다.트리는 이르케 생겼고 트리를
10.[자료구조]Tree - (8-2)
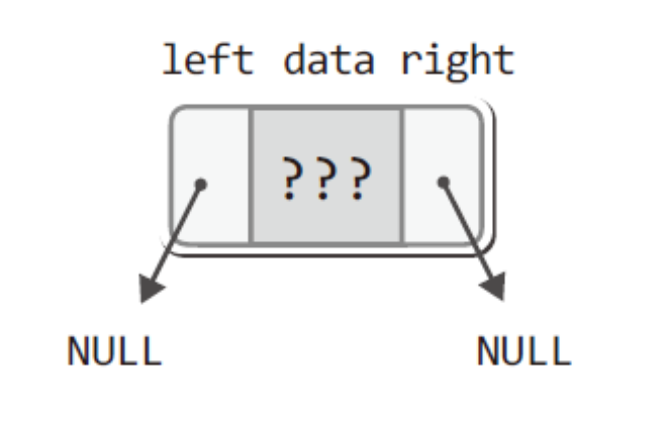
이진트리의 구현 방법 또한배열기반과 연결리스트 기반이 있다. 대체적으로 연결리스트 기반으로 하는 방식이 더 유연하지만 "완전 이진트리" (트리가 완성된 이후로는 그 트리로는 매우 빈번한 탐색이 이뤄진다)같은 경우라면 배열 기반이 연결 리스트에 비해서 탐색이 매우 용이하
11.[자료구조] 순회를 통한 트리 데이터의 소멸 8-3 문제
앞서 구현한 이진트리에는 소멸관련 함수가 없다.우린 소멸을 위해 순회를 배웠으니 ! 배운 내용들을 토대로 순회를 통한 동적으로 할당된 노드들을 소멸시키고 종료해보자.binaryTree.c 파일에이 코드를 추가해주면된다.그 이후 다른파일에도 참고 해주면된다.소멸시키는 함
12.[자료구조] 이진 트리의 순회 8-3
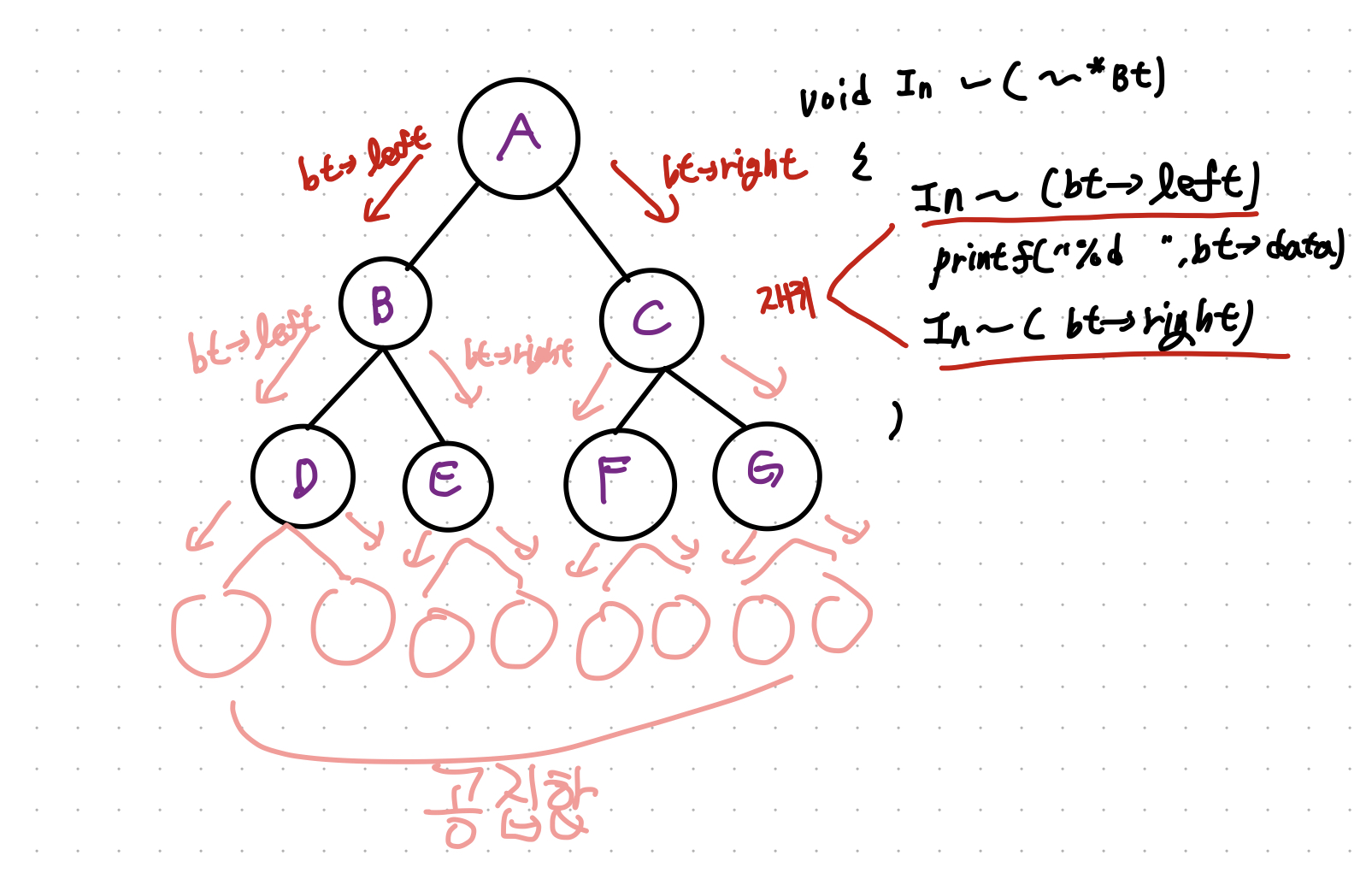
전위 순회 : 루트 노드를 먼저 !중위 순회 : 루트 노드를 중간에 !후위 순회 : 루트 노드를 마지막에 !이렇듯 이진트리를 순회하는 방법에는 "루트 노드를 언제 방문하느냐" 에 따라서 나뉜다. 이렇게 높이가 1인 트리의 순회는 어렵지 않는데..그 이상의 높이를 가진
13.[자료구조] 수식 트리(Expression Tree)의 구현 8-4
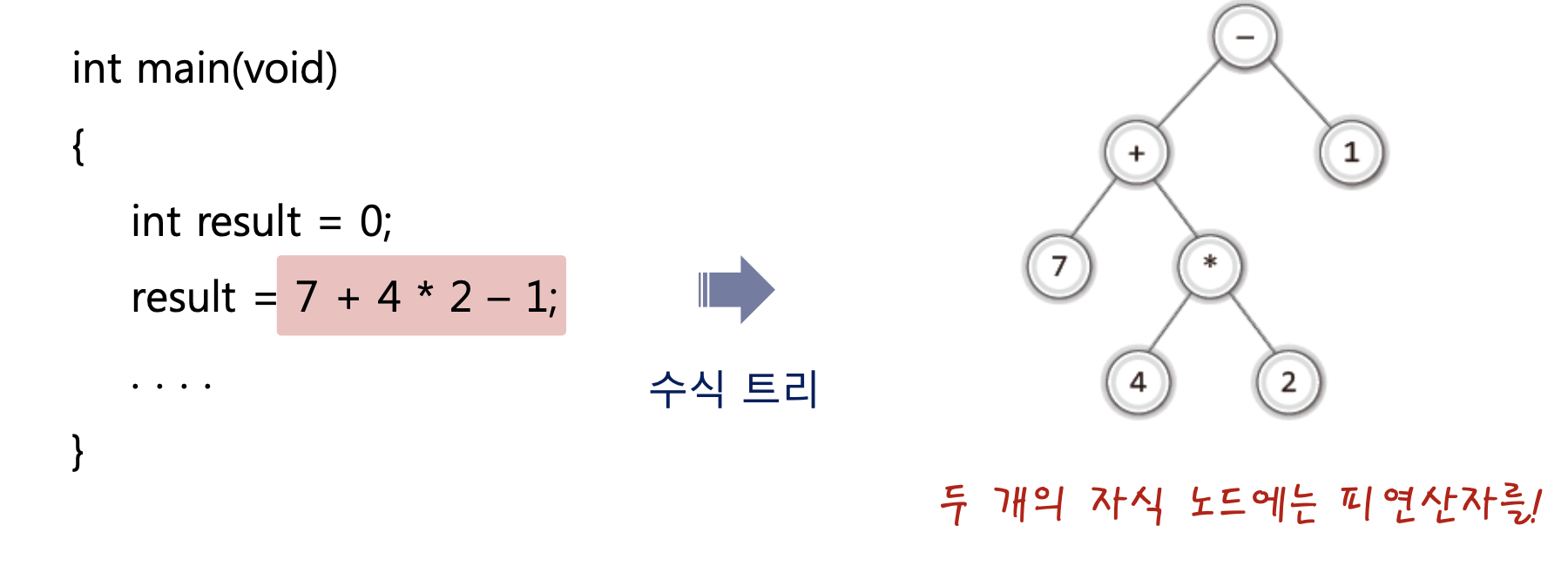
이진 트리에 대한 설명에 이어서이제는 이진 트리의 일종인 수식 트리에 대해 배워보자.앞에서는 이진 트리를 구성하는데 필요한 도구에 대해 만들었다면 이제는 이 도구를 이용하여 이진 트리의 일종인 "수식 트리"를 만들 것이다.이러한 방식으로 중위 표기법 수식을 컴퓨터가 알
14.[자료구조] 중위 표기법의 소괄호 문제 8 - 2
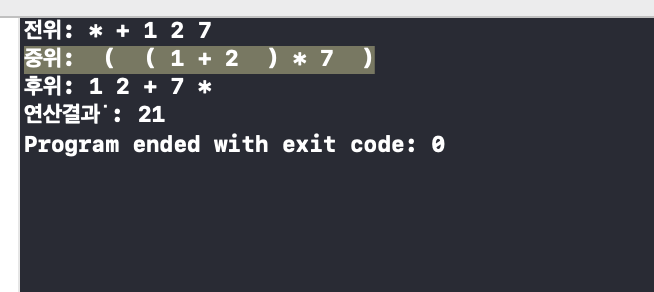
보통 자료구조 과목에서는 중위 표기법의 소괄호 출력까지는 신경을 쓰지 않지만....우리는 한번 구현해보자.중위 표기법에는 다음 세가지가 있다3 + 2 \* 73 + ( 2 \* 7 )( 3 + ( 2 \* 7 ) ) 연산자의 수만큼 소괄호를 구성하는 방법이 수식 트리에
15.[자료구조] 우선순위 큐(Priority Queue)와 힙(Heap) 힙의 구현과 우선순위 큐의 완성 9-2-1

힙의 구현은 곧 우선순위 큐의 완성으로 이어진다고해서 이 둘이 동일하다는것은 정확하지 않는것이다. 그러므로 구분할 수 있어야한다. >힙은 우선순위 큐의 구현에 어울리는, 완전 이진 트리의 일종이라는 사실을 기억해야한다. 힙에서의 데이터 저장과정 "마지막 위치"는
16.[자료구조]우선순위 큐(Priority Queue)와 힙(Heap) 힙의 구현과 우선순위 큐의 완성 9-2-2
우선 좋은 모델은 아니나 이해하기 용이한 방식으로 힙을 구현한 후 보다 합리적인 형태로 변경하자 ! 우선 헤더파일을 보자 SimpleHeap.h위의 파일은 순수한 힙의 구현을 위한 헤더파일이라고 하기보다는 우선순위 큐의 구현을 염두에 두고 정의한 헤더파일이다. 이것은
17.[자료구조]우선순위 큐(Priority Queue)와 힙(Heap) 힙의 구현과 우선순위 큐의 완성 9-2-4
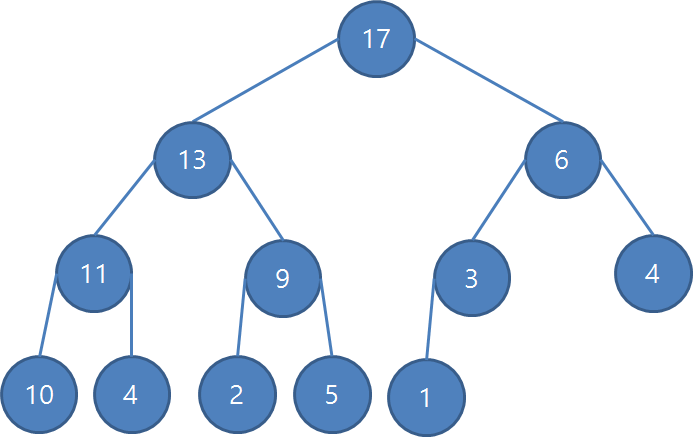
바로 우선순위 큐의 헤더,소스,메인 다보자 ! PriorityQueue.hPriorityQueue.cPriorityQueueMain.c
18.[자료구조] 우선순위 큐(Priority Queue)와 힙(Heap) 우선순위 큐의 이해 9-1

우선순위 큐는 이 이름에서 의미하듯이 큐와 관련있어서 "큐"를 확장하는 수준에 마무리 될 것 같지만.. 많은 차이가 있다.큐와 우선 순위 큐는 핵심연산이 enqueue dequeue 로 동일하지만..연산결과에는 차이가 있다.큐는 연산의 결과로 먼저 들어간 데이터가 먼저
19.[자료구조]우선순위 큐(Priority Queue)와 힙(Heap) 힙의 구현과 우선순위 큐의 완성 9-2-3
앞선 상황들의 문제의 해결을 위한 요구사항을 다음 한 문장으로 정리할 수 있다. 프로그래머가 우선순위의 판단 기준을 힙에 설정할 수 있어야 합니다.앞서 정의한 이 구조체를 변경해야한다.이 둘을 다음과 같이 하나의 구조체로 대신하자.가장 큰 변화는 구조체 HeapElem
20.[자료구조] 우선순위 큐의 활용

힙의 구현결과 : UsefulHeap.h,c우선 순위 큐의 구현결과 : PriorityQueue.h,cusefulHeap.h의 typedef 선언 변경typedef char HData; -> typedef char \* HData;Main.c
21.[자료구조] 포인터 함수
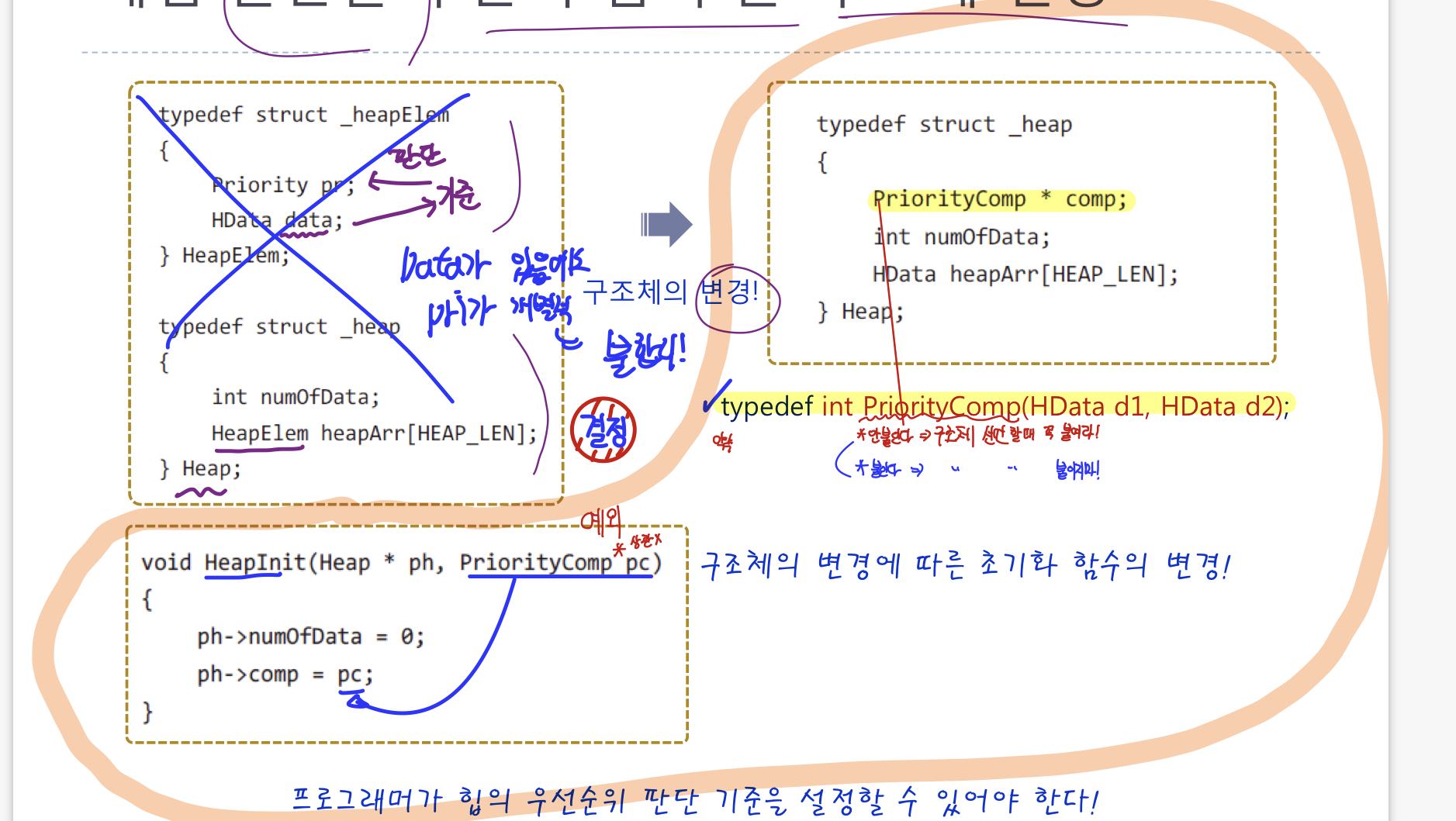
다른 곳에 세세히 설명 잘 되있겠지만, 내가 이해한것을 토대로 간편하게 보기위해 여기 남김!typedef 포인터 함수 선언시 \*를 붙이냐 안붙이냐에 따라서 구조체 정의가 달라질 수 있다.붙임 : 구조체 선언할때 꼭 붙인다.안붙임 : 구조체 선언시 붙이면 안된다. 파라
22.[자료구조] 정렬(Sorting) 10-1(버블정렬)
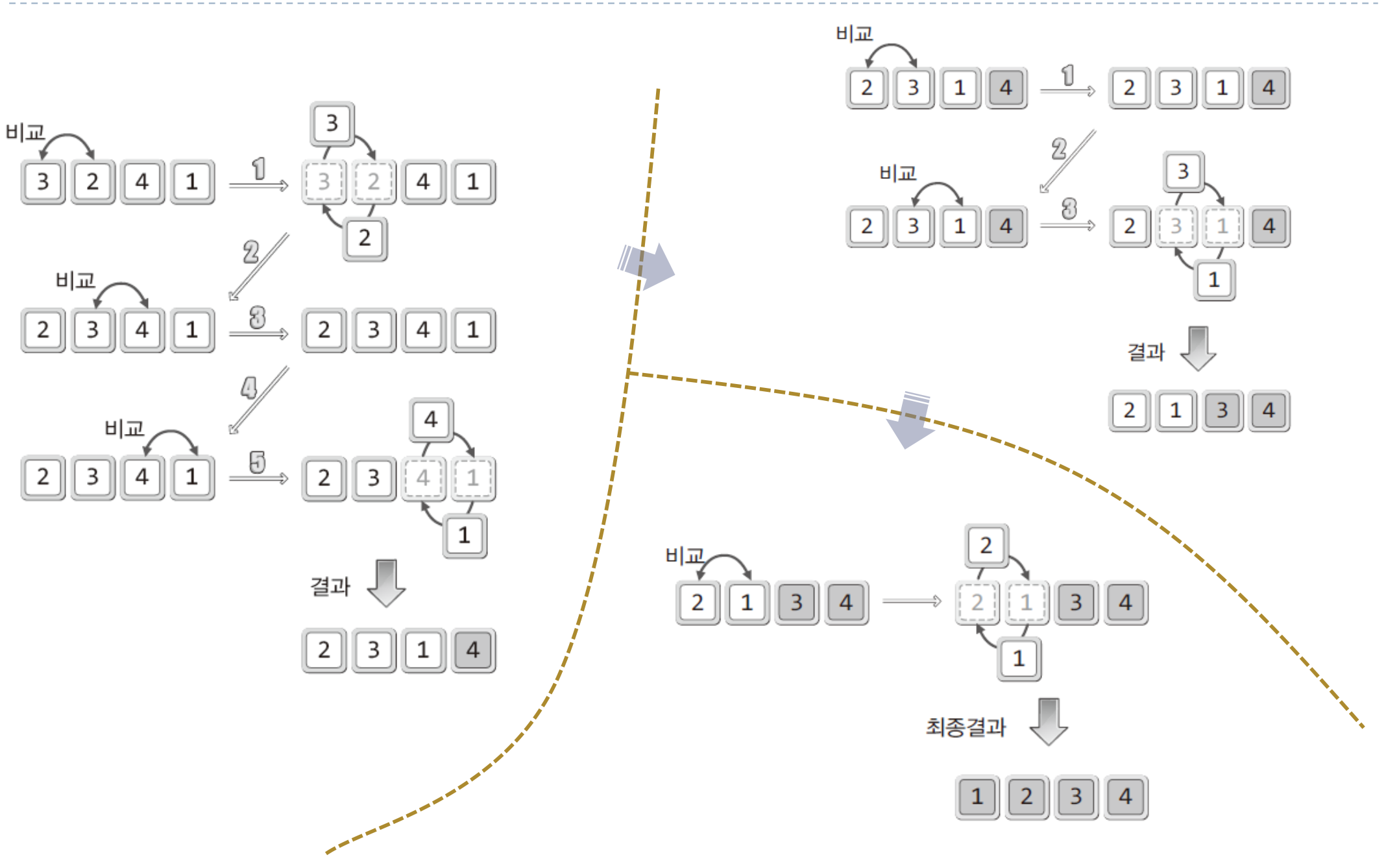
버블 정렬은 정렬의 대명사로 알려져 있는 만큼 이해하기도 구현하기도 쉽다. 하지만.. 그런만큼 성능에는 아쉬움이 있다.우선 버블 정렬의 과정을 보자 ! 이렇듯 버블 정렬은 인접한 두 개의 데이터를 비교해가면서 정렬을 진행하는 방식이다. 즉! "정렬의 우선순위가 가장 낮
23.[자료구조] 정렬(Sorting) 10-1(선택 정렬)
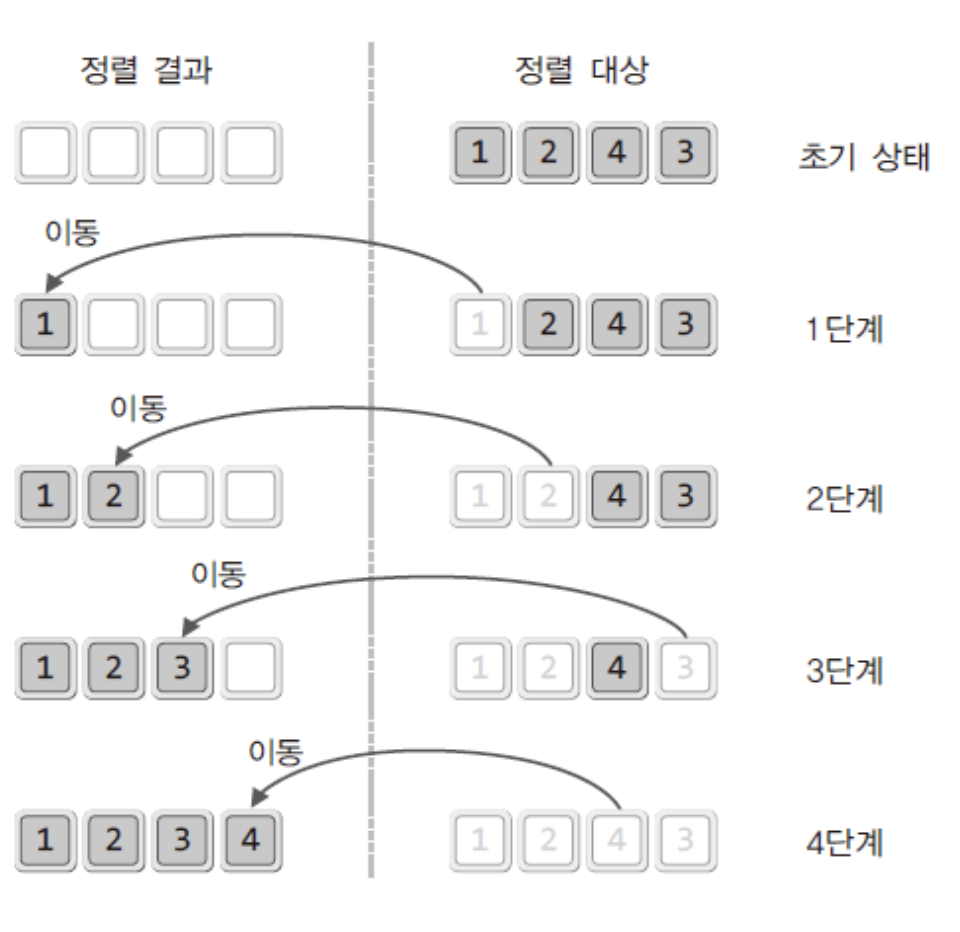
이번에 소개하는 선택정렬은 버블 정렬보다도 쉽고 간단한 알고리즘이다. 그림만 봐도 이해가 되지 않는가!?말 그대로 선택해서 정렬한다!그런데.. 보면 이런 생각이 들것이다"그럼 선택 정렬은 정렬결과를 담을 별도의 메모리 공간이 필요하겠네요!"위 그림 대로 진행한다면 그렇
24.[자료구조] 정렬(Sorting) 10-1(삽입 정렬)
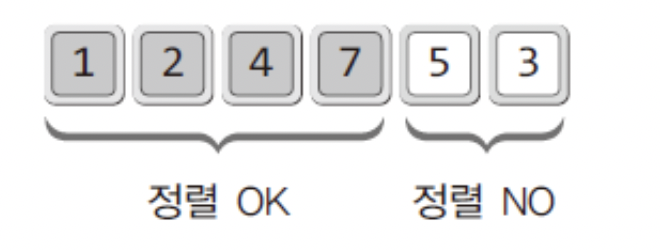
삽입 정렬은 보는 관점에 따라서 별도의 메모리를 필요로 하지 않는 "개선된 선택 정렬"과 유사하다고 느낄 수 있지만 전혀 다른 방법으로 정렬을 이뤄나간다.위 그림의 배열은 정렬이 완료된 부분과 완료되지 않은 부분으로 나뉘어 있다. 이렇듯 삽입 정렬은 정렬 되지 않은 부
25.[자료구조] 복잡하지만 효율적인 정렬 알고리즘 10-2(힙 정렬)
앞서 소개한 단순한 정렬 알고리즘은 정렬대상의 수가 적은 경우 효울적으로 사용할 수 있지만 정렬 대상의 수가 적지 않은 경우에는 아니다!그러므로 우리는 이 경우에서도의 만족스러운 결과를 보장하는 알고리즘이 필요하다.제목만 복잡하지만..이지! 사실상 앞서 설명한 정렬들이
26.[자료구조] 복잡하지만 효율적인 정렬 알고리즘 10-2(병합 정렬)
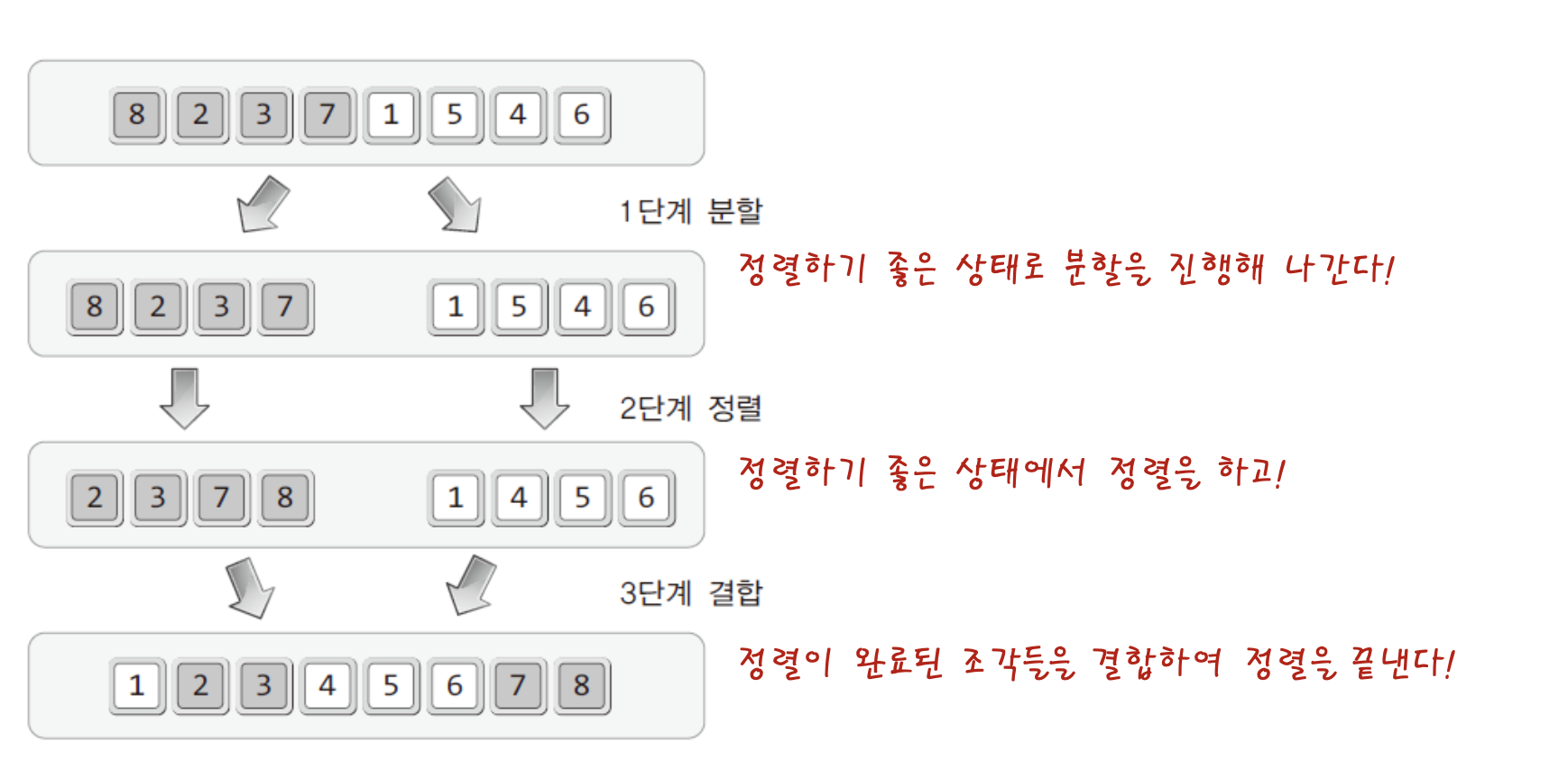
병합 정렬은 "분할 정복" 이라는 알고리즘 디자인 기법에 근거하여 만들어진 정렬 방법이다.분할 정복이란, 말 그대로 복잡한 문제를 복잡하지 않은 문제로 분할하여! 정복! 하는 방법이다.단!! 분할을 하고 정복까지 했으니 결합의 과정을 거쳐야 완성된다1 단계 분할 : 해
27.[자료구조] 복잡하지만 효율적인 정렬 알고리즘 10-2(퀵 정렬)

이번 퀵 정렬도 앞서 본 병합 정렬과 마찬가지로 "분할 정복"에 근거하여 만들어진 정렬 방법이다.실제로 이 또한 정렬대상을 반씩 줄여나가는 과정을 포함한다."퀵 자가 들어가는 걸 보면 제법 빠른 정렬인가봐요..? 그럼 그만큼 어렵겠쥬..?" 라는 생각을 할수 있지만 아
28.[자료구조] Median of three - 퀵 정렬
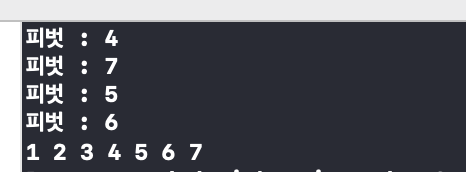
printf 를 추가해주면 선택된 피벗이 무엇인지, 정렬과정에서 몇 개의 피벗이 선택되었는지 확인할 수 있다.이와 같이 ! 선택된 피벗의 수는 정렬의 효율을 가늠하는 기준이 된다. 그럼 다음 배열로 설정해보자 . int arr15 = {1,2,3,4,5,6,7,8
29.[자료구조] 복잡하지만 효율적인 정렬 알고리즘 10-2(기수 정렬) - 1

퀵 정렬까지 알고 나면 그 나름의 만족감에 더 이상의 정렬 알고리즘에는 관심이 가지 않는 다는 말이 많다!하지만! 기수 정렬 알고리즘은 다음과 같은 특징이 있다."정렬 순서상 앞서고 뒤섬의 판단을 위한 비교연산을 하지 않는다."비교연산은 정렬 알고리즘의 핵심이다.특히!
30.[자료구조] 복잡하지만 효율적인 정렬 알고리즘 10-2(기수 정렬) - 2
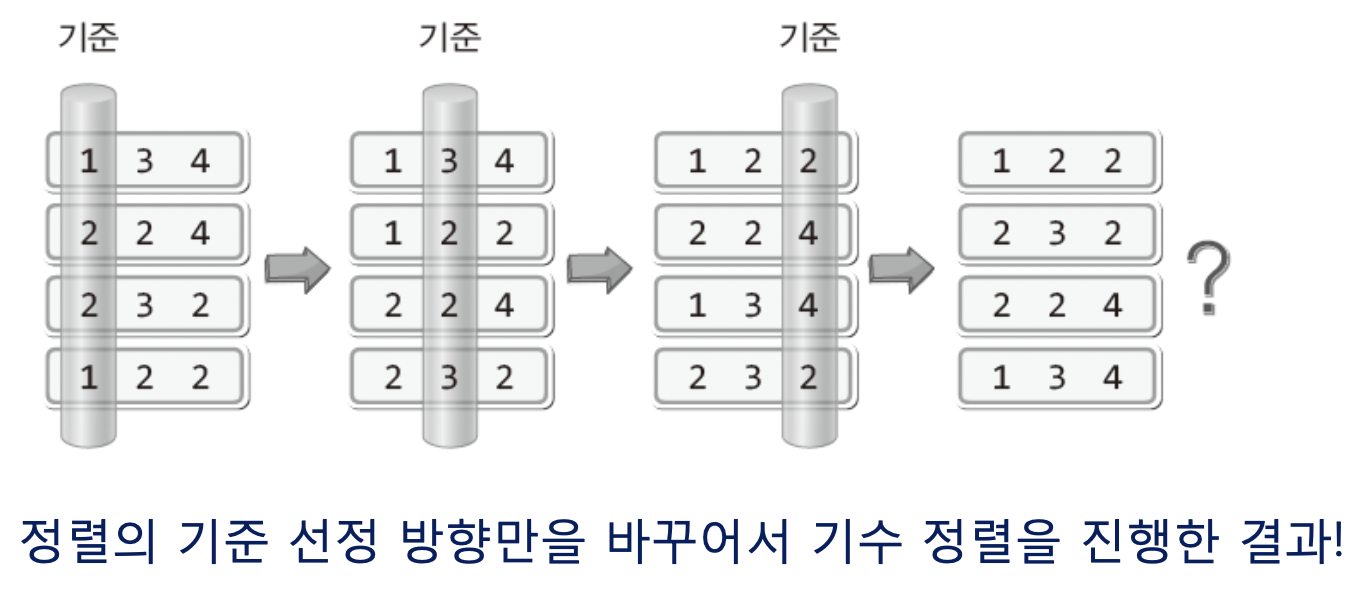
앞서 설명한 LSD와 반대로MSD는 Most Significant Digit의 약자로써 가장 중요한 자릿수, 다시말해서 가장 큰 자릿수부터 정렬이 진행된다는 의미를 담고 있다."그럼 LSD와 방향만 다르고 정렬과정은 같나요!?" 안타깝지만.. 아니다..이를 확인하기위해
31.[자료구조] 탐색(Search) 1 - 탐색의 이해와 보간 탐색(11-1)
탐색의 이해 탐색 다시말해서 "데이터를 찾는 방법"이다. >탐색은 트리의 뒷 이야기에 해당한다. 탐색은 알고리즘보다 자료구조에 더 가까운 주제이다! 이유는 >"효율적인 탐색을 위해서는 "어떻게 찾을까"만을 고민해서는 안되고 "효율적인 탐색을 위한 저장방법이 무엇일까"
32.[자료구조] 탐색(Search) 1 - 이진 탐색 트리 (11-2)
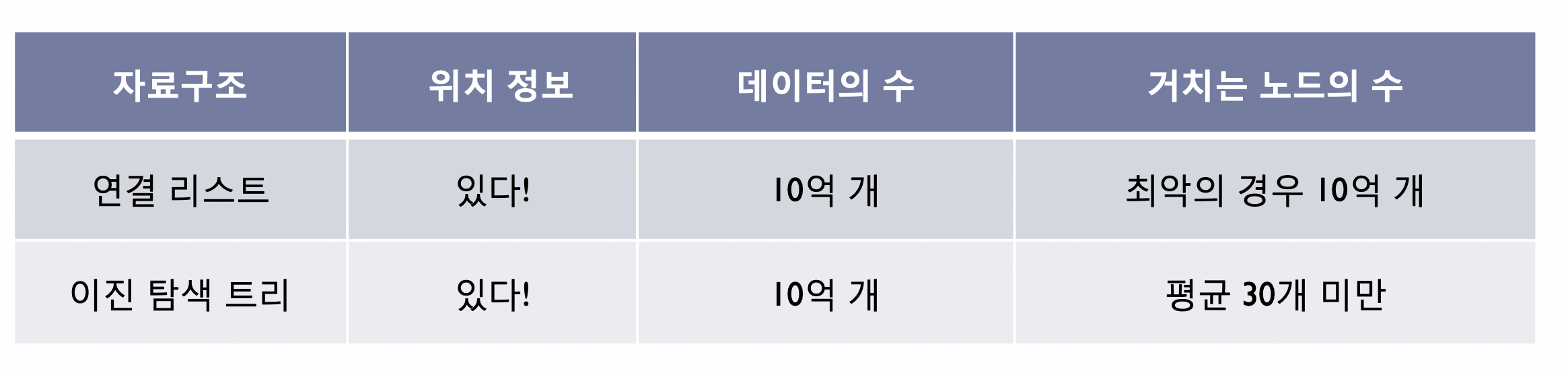
이진 트리의 구조를 보면, 트리는 탐색에 효율적이라는 사실을 쉽게 알 수 있다. 저장된 데이터의 수가 10억 개 수준에 이른다 해도!!트리의 높이는 30을 넘지 않기 때문이다!!우리가 찾는 데이터가 리스트의 정중앙에 위치한다는 정보를 가지고 있음에도 10억개의 노드중
33.[자료구조] 탐색(Search) 1 - 이진 탐색 트리의 조건 - 11-1 문제
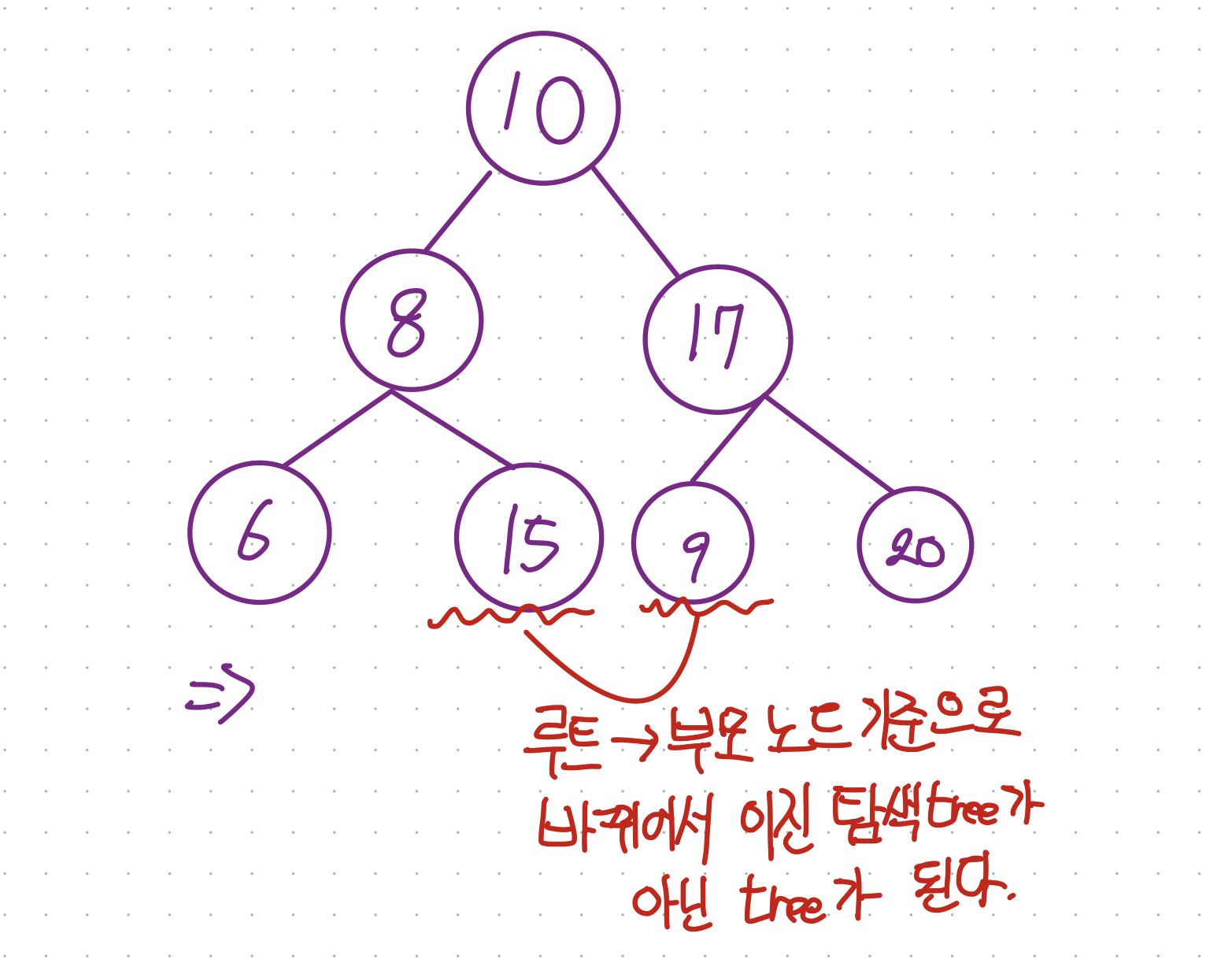
앞서 이진 탐색 트리의 노드에 저장된 키는 유일하다.루트 노드의 키가 왼쪽 서브 트리를 구성하는 어떠한 노드의 키보다 크다.루트 노드의 키가 오른쪽 서브 트리를 구성하는 어떠한 노드의 키보다 작다.왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.을 설명했다그리고왼쪽 자식
34.[자료구조] 탐색(Search) 1 - 이진 탐색 트리 (11-2-2) 삽입

구현에 앞서 우리는 구현방법을 결정해야 한다.다음 두 가지중 한가지 방법을 선택하자 ! 구현 방법 1 이전에 구현한 이진 트리를 참조하여 처음부터 완전히 다시 구현한다. 구현 방법 2 이진 탐색트리도 이진 트리이니, 이전에 구현한 이진 트리를 활용하여 구현한다. 첫번째
35.[자료구조] 탐색(Search) 1 - 이진 탐색 트리 (11-2-2) 탐색
자 ! 이제 이어서 탐색을 담당하는 BSTSearch 함수를 보자 ! 탐색의 과정은 삽입의 과정을 근거로한다 ! while 문에서 비교대상의 노드보다 값이 작으면 왼쪽/크면 오른쪽으로 이동 하고 있다.이렇게 반복문안에서 계속해서 이동하다가 target==cd가 되면 r
36.[자료구조] 탐색(Search) 1 - 이진 탐색 트리 (11-2-3) - 삭제 - 1
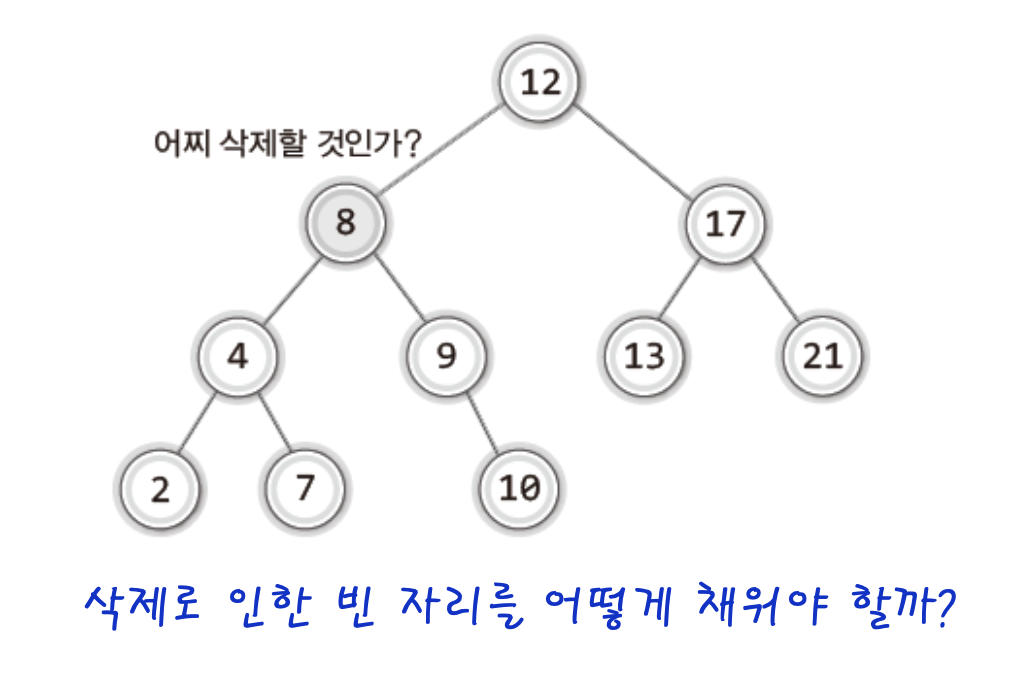
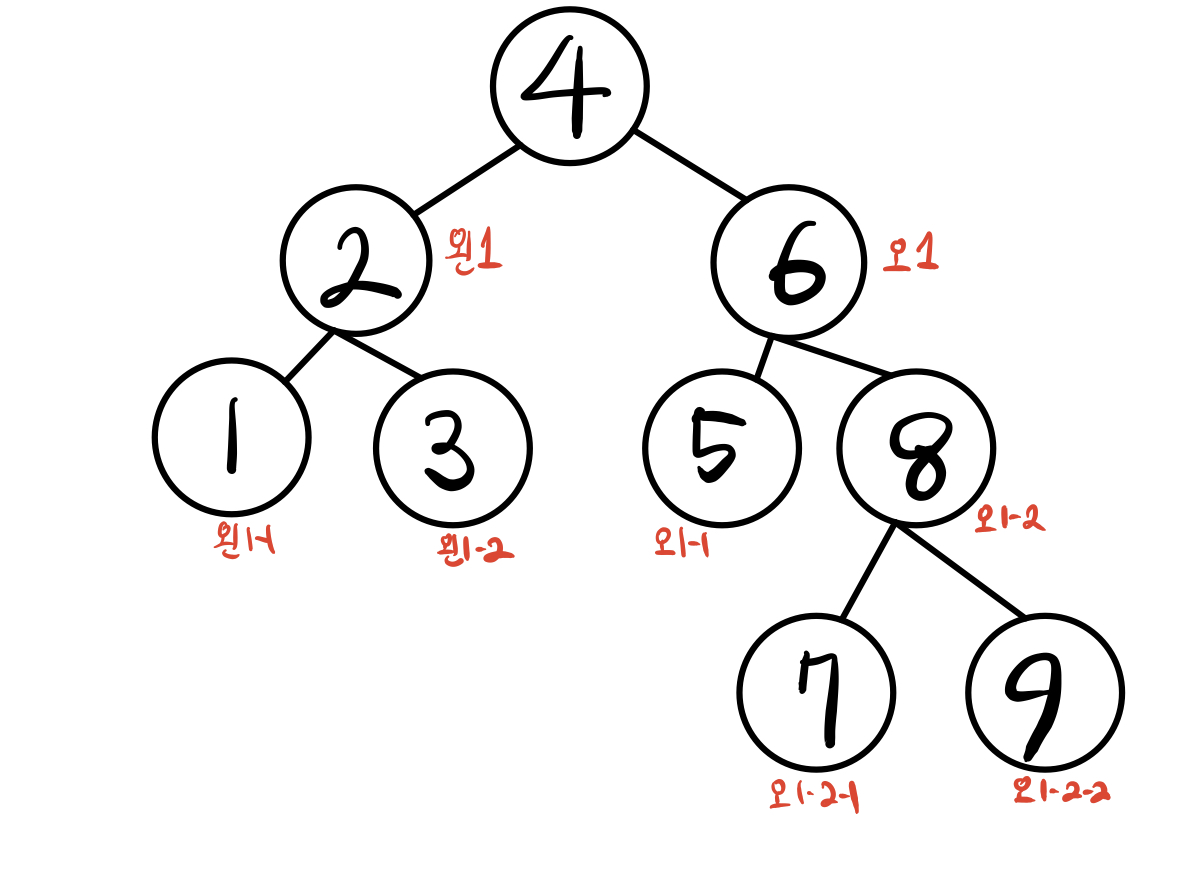
이제 대망의 삭제에 대해 배워보자 ! 위 그림에서 8을 삭제한다고 하면 삭제 한 후 이 자리를 누군가 대신 채워여만 이진 탐색 트리가 유지되므로 어떻게 이 빈자리를 채워야 할지가 이진 탐색트리의 삭제가 어랴운 이유중 하나이다.단말노드라면 그저 삭제하면 되지만 아니라면
37.[자료구조] 탐색(Search) 1 - 이진 탐색 트리 (11-2-4) - 삭제 - 2

이를 구현 하기 위해 BinaryTree2.h,c에 다음 4개의 함수를 추가로 선언 및 정의하자 우선 BinaryTree2.c 는 이진 탐색 트리 구현에 충분한 도구가 되지는못하는데 그 이유는 다음 두 가지이다. 노드의 제거에 대한 기능이 정의되지 않았다.MakeLef
38.[자료구조]탐색 2 (12-1-1) AVL트리,LL회전
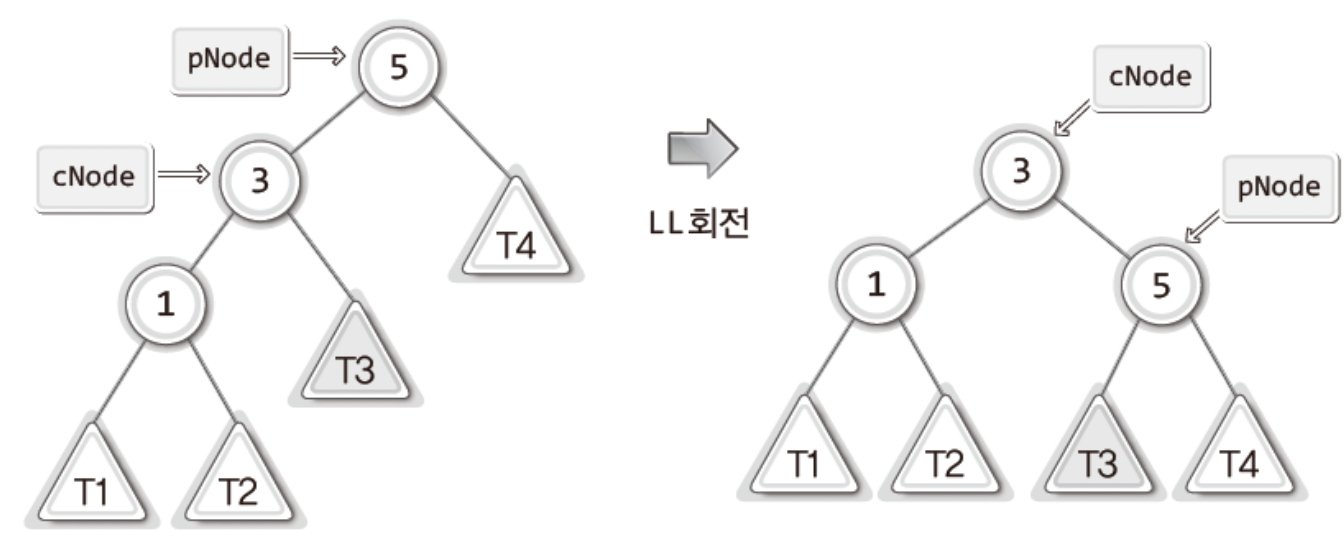
이제 ! 탐색1을 끝마쳤으므로 탐색2를 배워보자.제일 첫 챕터는 이다.이진 탐색 트리의 탐색 연산은 로그이엔의 시간 복잡도를 가지지만..균형이 맞지 않게 쌓여수록 빅오는 n에 가까운 시간 복잡도를 보인다.그림을 보면 노드의 수 만큼 높이가 형성된거와 같이 매우 불균형해
39.[자료구조]탐색 2 (12-1-2) RR회전
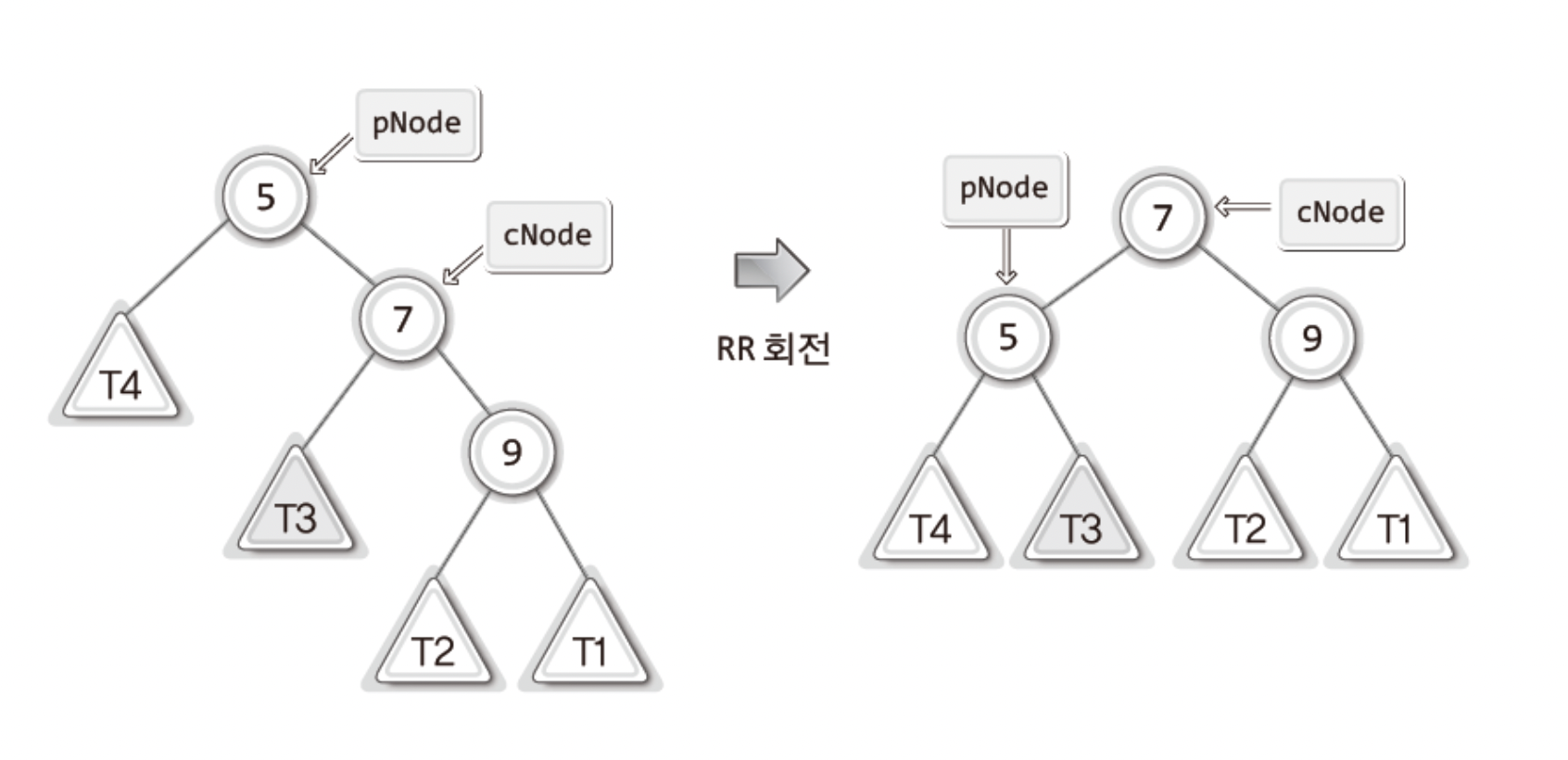
이제 어느정도 눈치가 있다면!RR회전은 Right Right 상태의 이진 탐색 트리를 회전시킨다는것임을 알것이다!그리고 이것은"RR상태와 LL상태의 차이점,회전의 유일한 차이점은 방향아닌가요?" 라는것에!맞다!! 유일한 차이점은 방향이다!!! 참고로 LL회전을 가리켜
40.[자료구조]탐색 2 (12-1-3) LR,RL회전
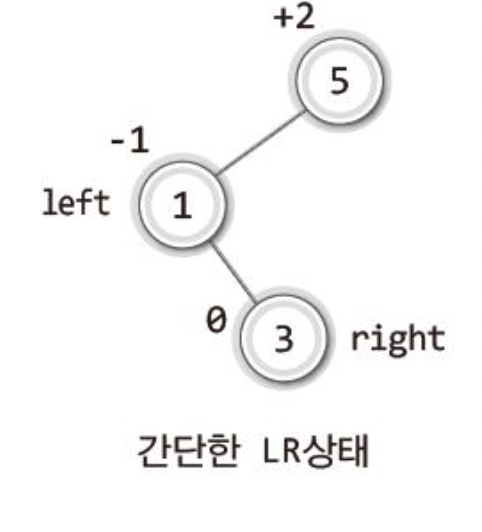
이제 LR을보고..아!"LR회전이란 LR상태에서의 리밸런싱을 위한 회전방법이겠군!?"이라고 짐작하여 "LR상태는 자식 노드가 왼쪽 하나! 그리고 이어서 오른쪽 하나 달린 상태를 뜻하겠군!!"이라고 웬만한 눈치가 있다면 생각할것이다!정답이다!!이제 이 상태를 그림으로 보
41.[자료구조]탐색 2 (12-2-1) 높이계산 도구

이렇게 구현과 이해를 구분한 이유는 이해만으로도 매우~ 의미 있기에 그랬다! 그러니 이제 이 의미있는 것을 구현해보자! 이또한 이진탐색트리이므로 BinaryTree3.hBinaryTree3.cBinarySearchTree2.hBinarySearchTree2.h를 확장해
42.[자료구조]탐색 2 (12-2-1) LL/RR회전 도구
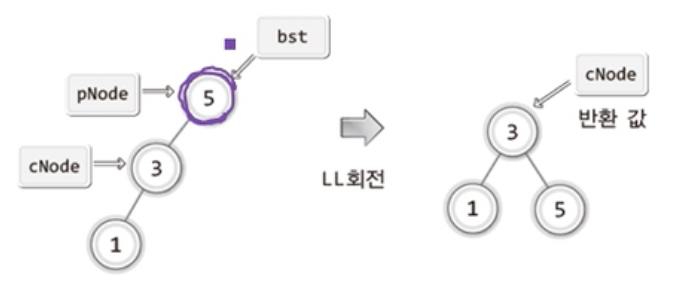
LL회전은 어떻게 진행될까?앞선 포스트들을 잘 보아왔다면 충분히 생각해낼수 있고개념의 이해일때 추가해야할 함수도 생각했었다.그러니 바로 코드를 짜보자 ! 어떤가 !그저 pNode,cNode를 생성 후 초기화를 진행중이고 앞서 구현한 회전 도구들을 이용한 후 ! 루트 노
43.[자료구조]탐색 2 (12-2-2) LR/RL회전 도구
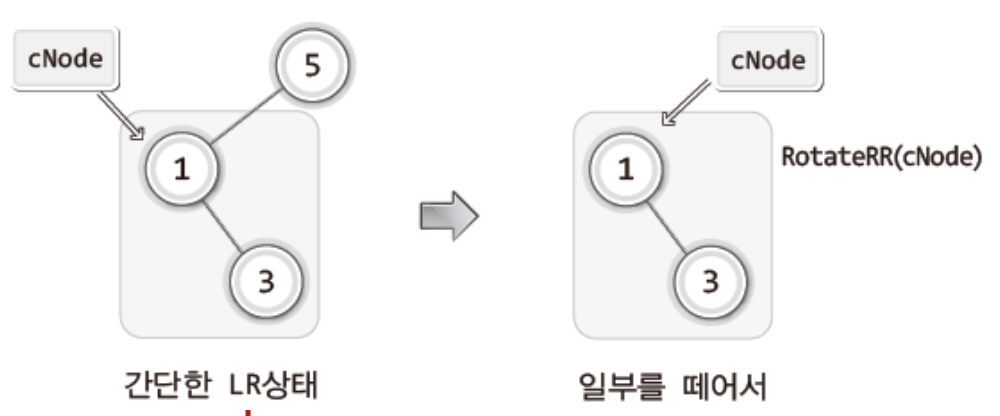
도구를 구현하기 앞서 우리는 LR회전 : 부분적 RR회전에 이어서 LL회전을 진행한다.RR회전 : 부분적 LL회전에 이어서 RR회전을 진행한다.그럼 바로 LR회전을 담당하는 함수의 구현을 보자어떤가!생각보다 간단하지 않는가?!앞서 LR회전을 위해서는 부분적RR회전후 전
44.[자료구조]탐색 2 (12-2-3) Rebalance 함수
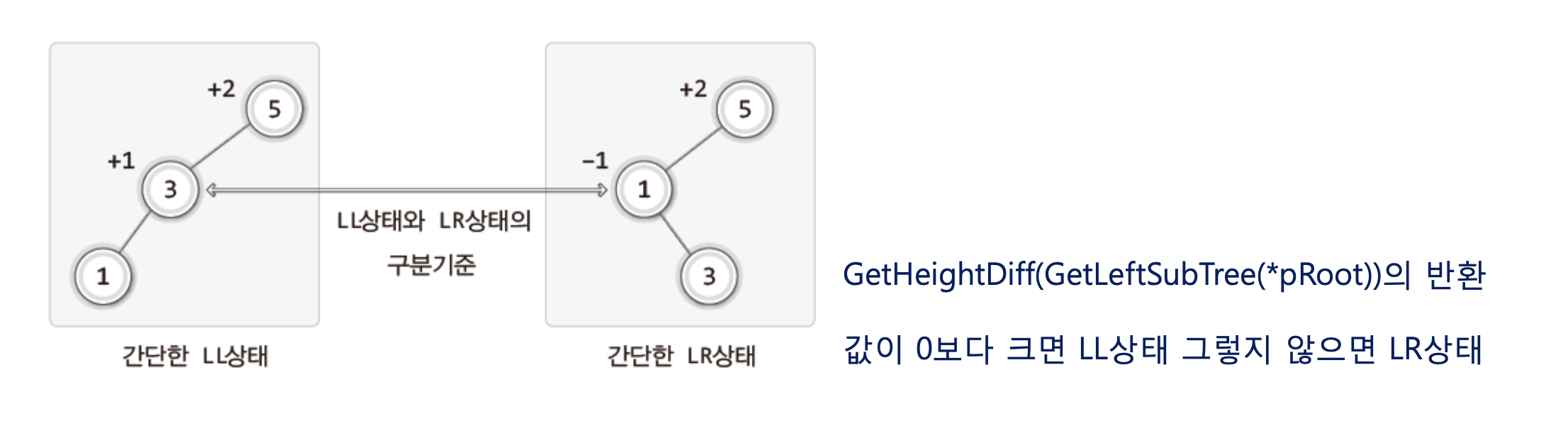
이제 기본적인 도구들이 마련되었으니 이 많은 도구들을 사용하기 위한 도구의 사용순서 및 사용시기를 모두! 다음 도구를 하나 더 만들자!\+2 이상이면 LL/LR 이고 -2이하이면 RR/RL 이다.그럼 이제 LL 와 LR을 구분하는 방법을 정리해보자 ! 어떤가! 루트노드
45.[자료구조]탐색 2 (12-2-4) AVL트리의 구현
이제 만든 도구들을 모아둔 헤더/소스 파일을 보이겠다 ! AVLRebalance.hAVLRebalance.c이렇듯 헤더파일에는 필요한 선언만 하는것이 코드를 깔끔하게 쓸 수 있는 팁? 이다! 기존에 Insert/Remove 함수에 노드 추가 후 리밸런싱으로 그저 끝을
46.[자료구조] 테이블과 해쉬 - 1
이번 내용도 탐색과 관련되있어 앞선 탐색1,2의 연장으로 볼 수 있지만!!!!트리와 관련된 어떠~한 것도 언급되지않는다!!!!오예!!!!AVL트리는 탐색과 관련하여 매우! 만족스러운 성능을 보였지만.... 탐색 키의 비교과정을 거치는 과정이 찾는 대상에 가까워지는 방식
47.[자료구조] 테이블과 해쉬 - 2
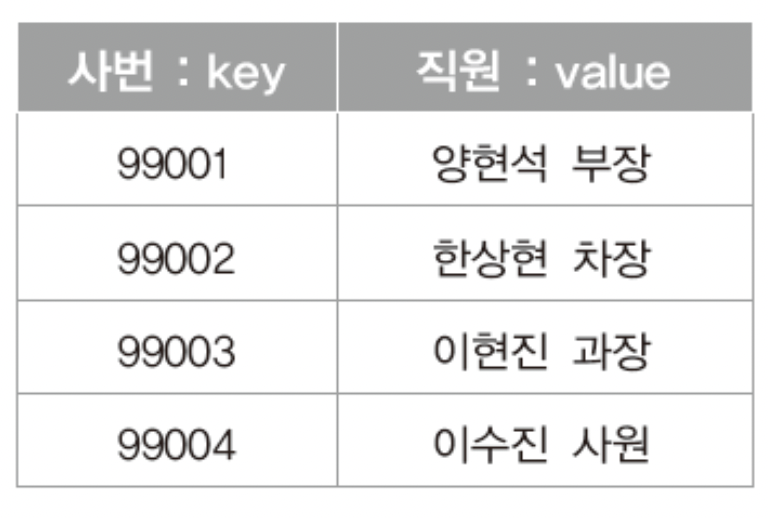
앞선 테이블에서의 문제점을 정리하자면 직원 고유번호의 범위가 배열의 인덱스 값으로 사용하기 적당하지 않다.직원 고유번호의 범위를 수용할 수 있는 매우 큰 배열이 필요하다.그렇기에 우리는 해쉬 함수를 활용해 이 문제점들을 해결할려고한다.이 함수를 소개하기전 앞서 보인 예
48.[자료구조] 테이블과 해쉬 - 3
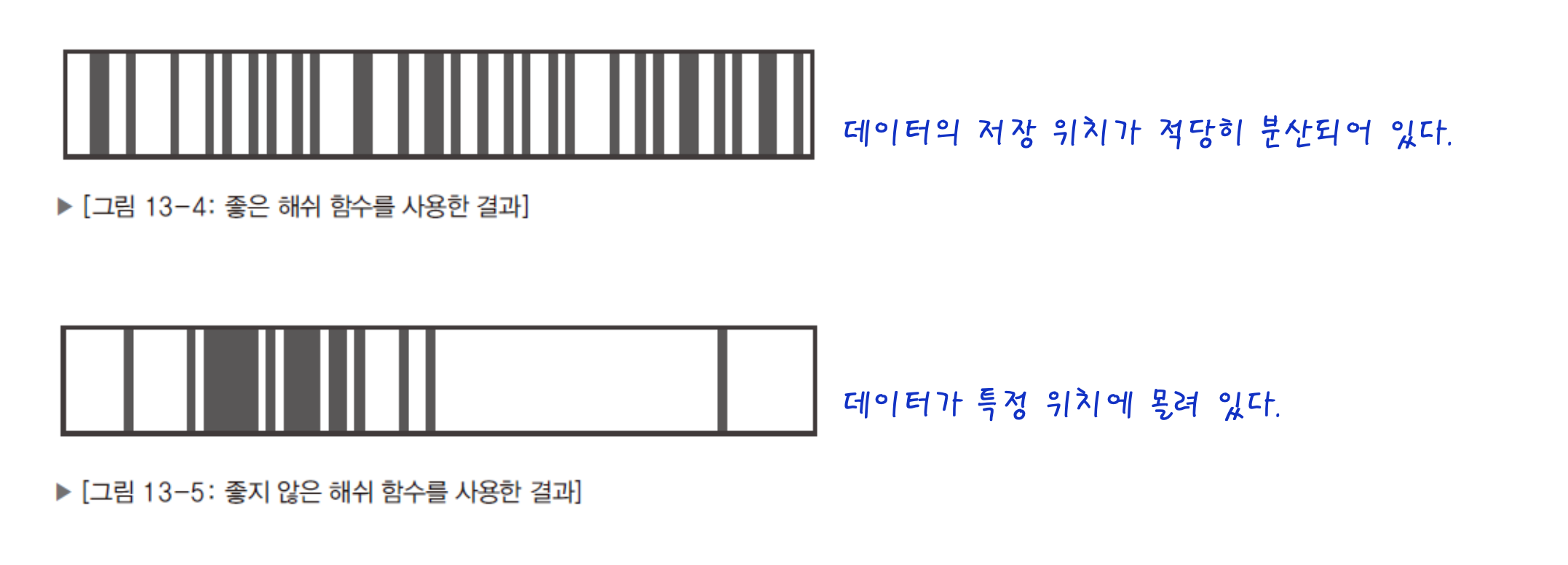
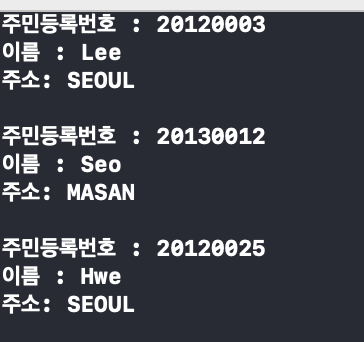
좋은 해쉬함수의 조건을 언급하기에 앞서 좋은 해쉬함수와 좋지 않은 해쉬함수의 차이점을 보여주겠다.이렇듯 좋은 해쉬함수는 골고루 데이터들이 분포되어있어 "충돌" 발생 확률이 낮다.그에 반해서 좋지 못한 해쉬함수는 데이터가 몰려있어 충돌할 확률이 높다.이렇듯 좋은 해쉬함수
49.[자료구조] 테이블과 해쉬 - 4

충돌문제해결이라는것은 생각외로 우리가 생각하는 수준에서 벗어나지 않는다!충돌이 발생하면 그 자리를 대신할 자리를 찾는 방법을 찾는것이니깐 말이다!!해쉬 함수 f(x)가 있고 테이블의 내부 저장소가 배열이라고 가정하면 이와 같다!말그대로 선형적이며 충돌이 발생하면 충돌발
50.[자료구조] 테이블과 해쉬 - 5

앞서 우리가 배운 방법들을 가리켜"열린 어드레싱 방법(Open addressing Method)"라고 하는데 이는 충돌이 발생하면 다른 자리에 대신 저장한다는 의미가 담겨 있다.반면, 이번에는 "닫힌 어드레싱 방법(closed addressing method)"이라 한
51.[자료구조] 그래프 - 1(그래프 이해와 종류)
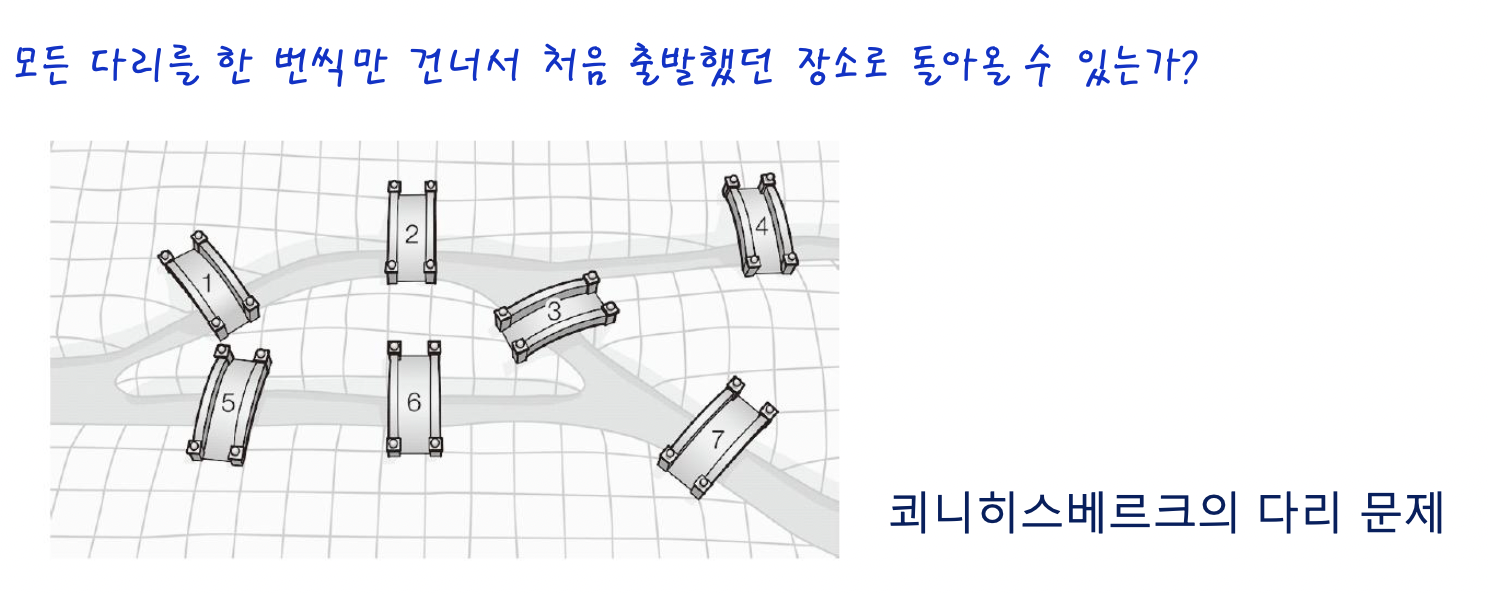
드디어 마지막 챕터이다..그래프만 끝내고 이제 쉬자!!!!!는 개뿔....c++/알고리즘문제/java 가 남아있다..ㅇㅁㅇ 집인데 집가고싶당.....그럼 마지막 챕터 그래프를 시작하겠다.그래프 알고리즘은 수학자 '오일러'에 의해 고안됬다.오일러는 이 문제를 해결하기 위
52.[자료구조] 그래프 - 2(인접 리스트 기반의 그래프 구현)
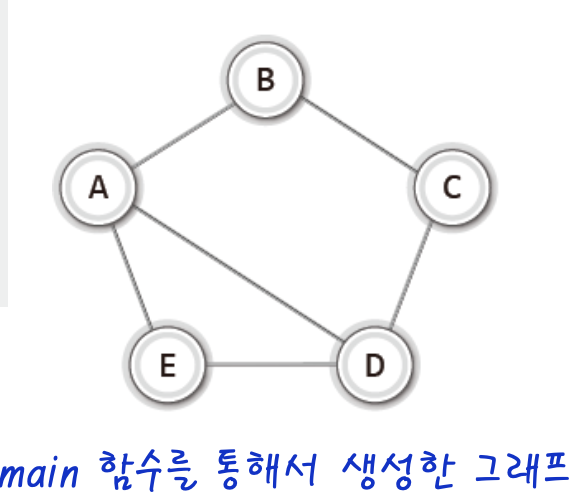
구현 해보일것인데 우리는 인접 리스트 기반의 그래프를 구현해보자.그 중 무방향 그래프를 할것인데 그 이유는 방향 보다 연결 리스트에 추가해야 하는 노드의 수가 두 배 더 많기 때문이다.자 ! 바로 헤더파일을 정의해보자ALgraph.h이 중 enum {A,B,C,D,E.
53.[자료구조] 그래프 - 3(그래프의 탐색)
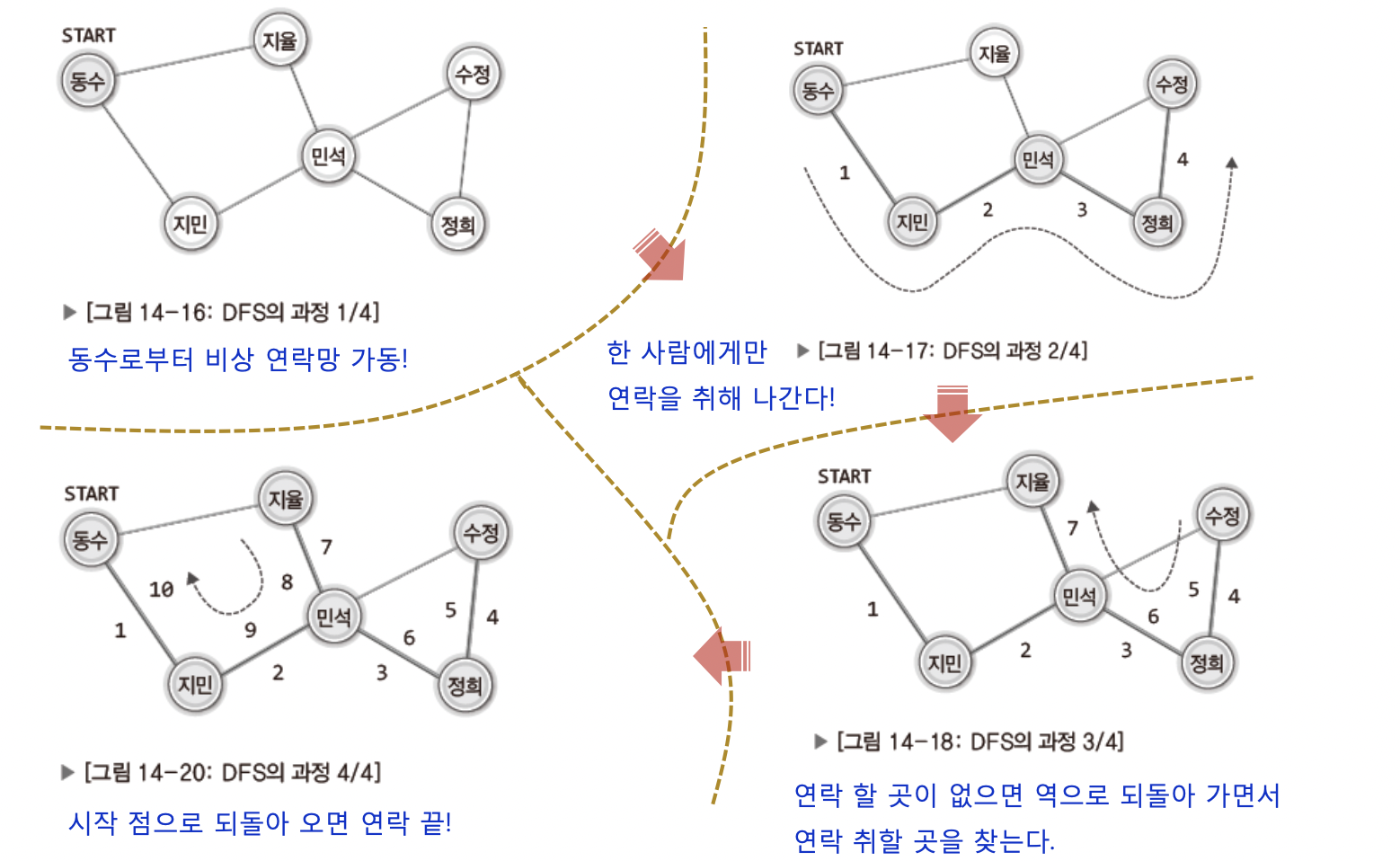
그래프 또한 탐색을 해야한다!그래프의 탐색과정은 어떻게 진행될까?모든 정점을 돌아다니려면 어떻게 해야할까?그래프의 탐색에는 별도의 정점을 모두 돌아다니기 위한 별도의 알고리즘 두 가지가 있다.깊이 우선 탐색(Depth Frist Search : DFS)너비 우선 탐색(
54.[자료구조] 그래프 - 4(그래프의 탐색) DFS 구현
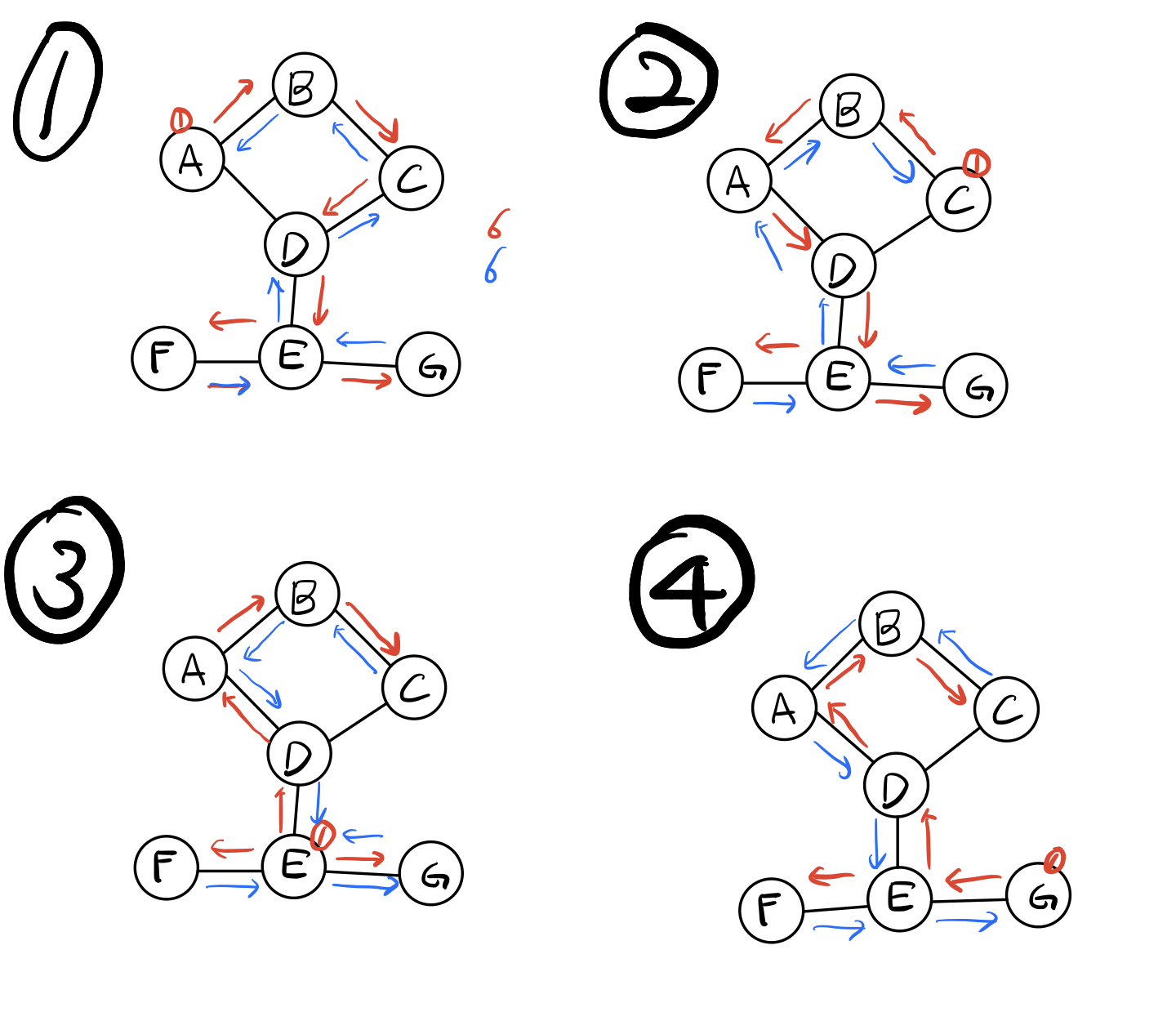
구현하기 위해서는 ALGraph.c,h 그래프ArrayBaseStack.c,h 스택DlinkedList.c,h 연결리스트DFSMain.c 가 필요하다ALGraphDFS.h 부터 보자 구조체에 visitInfo 맴버가 추가 됐는데 이 이유는 탐색이 진행된 정점의 정보를
55.[자료구조] 그래프 - 5(그래프의 탐색) BFS 구현
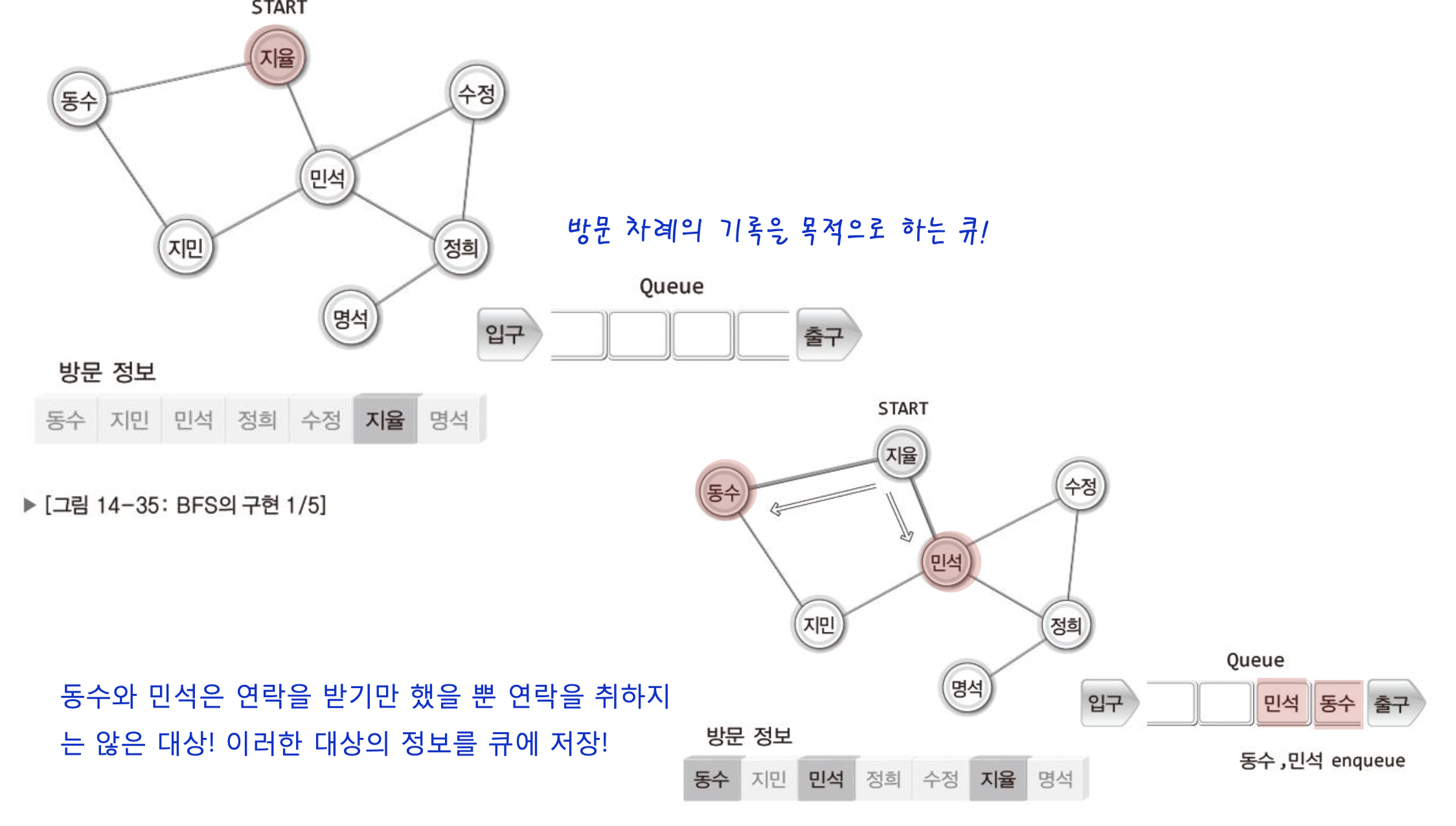
BFS는 DFS와 다르게 스택이 아닌 큐를 활용한다.그러므로큐 : 방문 차례의 기록을 목적배열 : 방문 정보의 기록 목적 이 두개가 필요하다.우선 그림으로 이해 해보자이렇게 지율이 부터 시작한다면 지율이는 동수와 민석이에게 연락을 취할것이다. 그럼 이 연락을 받은 동
56.[자료구조] 그래프 - 6 (최소 비용 신장 트리)

마지막은 그놈의 트리가 또 등장했다.망할놈,,,..... 사실 트리는 그래프의 한 유형이기에 그래프에서 등장하는것이다.이와 같이 두개의 정점을 잇는 간선을 순서대로 나열한 것을 가리켜 "경로"라고 하고 동일한 간선을 중복하여 포함하지 않는 경로를 가리켜 "단순 경로"라
57.[자료구조]그래프 - 7 (크루스칼 알고리즘의 구현) 자료구조 끝 !!!
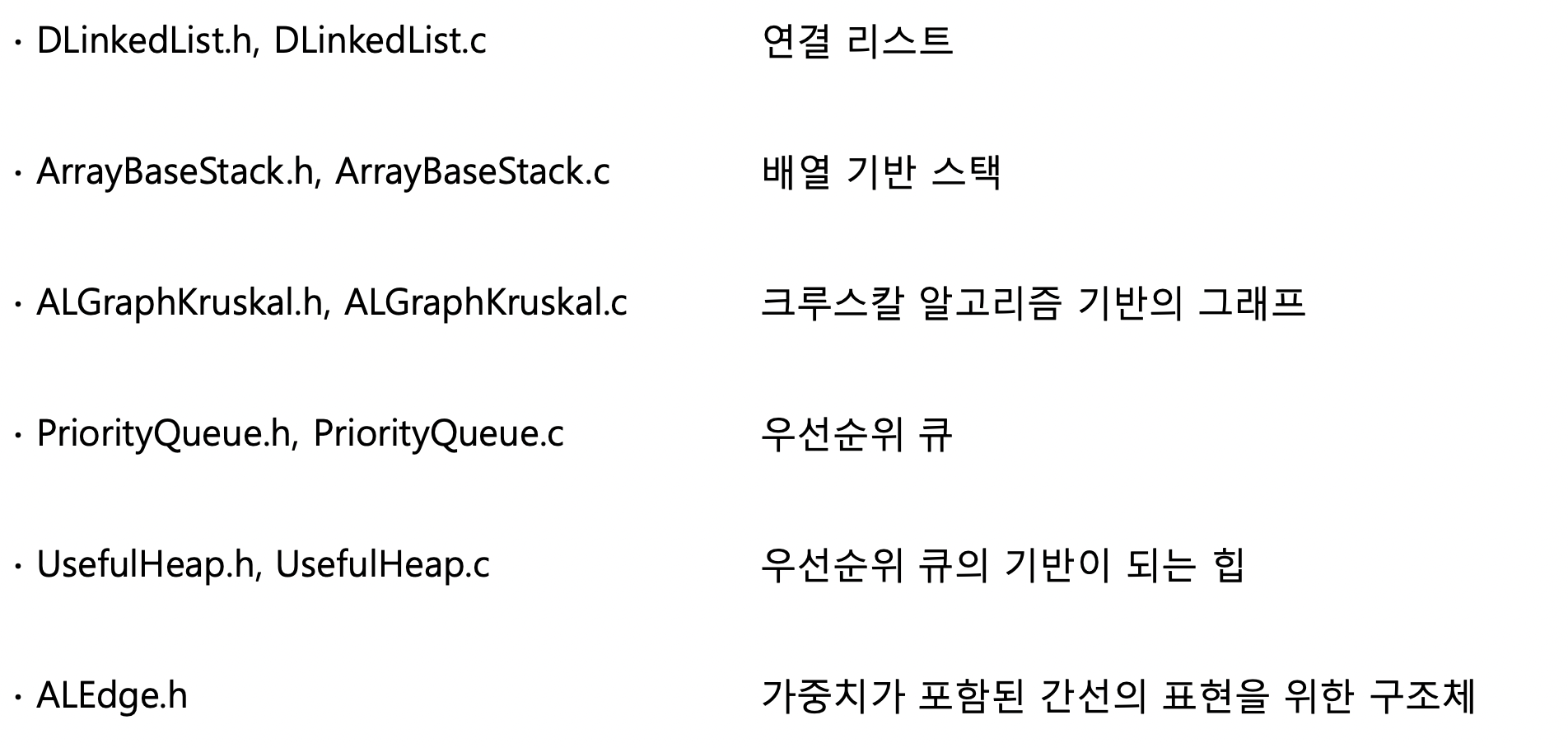
크루스칼 알고리즘은 다음과 같다."가중치를 기준으로 간선을 내림차순으로 정렬한 다음 높은 가중치의 간선부터 시작해서 하나씩 그래프에서 제거하는 방식"이전에 구현한 것들을 최대한 활용해보자!!!이를 위해 DFS 구현결과인 다음 파일을 활용하자DLinkedList.h,c