이진 탐색 트리의 헤더파일
구현에 앞서 우리는 구현방법을 결정해야 한다.
다음 두 가지중 한가지 방법을 선택하자 !
- 구현 방법 1
이전에 구현한 이진 트리를 참조하여 처음부터 완전히 다시 구현한다.- 구현 방법 2
이진 탐색트리도 이진 트리이니, 이전에 구현한 이진 트리를 활용하여 구현한다.
첫번째 방법을 이용하면, 앞서 공부한 이진 트리의 코드를 이해 없이 바로 분석할 수 있다.
반면!!
두번째 방법에는
- "이진 탐색 트리가 이진 트리의 확장이라는 사실을 코드 레벨에서 확인할 수 있다.
- "앞서 구현한 이진 트리를 점검하는 기회가 된다. 이진 트리의 ADT를 통해서 정의한 함수들이 기능적으로 부족하다면 이에 대한 반성 및 개선의 기회가 된다. "
- " 이진 트리를 활용한 이진 탐색 트리의 구현을 경험하는 것은, 좋은 프로그래밍 모델을 경험하는 기회도 된다."
이라는 장점이 있다.
그렇다면 어떤 방법을 선택해야할지 바로 뙇! 알지 않겠는가!?
바로 두번째 방법이다.
이 방법이 우리가 흔히 말하는 " 프로그래밍을 구조적으로 잘하는 사람"들이 선택하는 방법이다!
(이렇게 자료구조에서는 이미 만들었던것을 활용하는 것이 매우 중요한것같다 ! )
자!
이진 탐색 트리를 위해서는
- BinaryTree2.h,c 파일이 필요하다.
기억이 안날수도 있으니 BinaryTree2.h 에는

이 함수들이 선언되어있다.
옛날에 저자가 했던 말이 생각나는가?
"위에서 소개한 함수들은 이진 트리를 만드는 "도구"로써 정의된 것이다. 도구인 이 함수들을 이용해서 이진 트리르 구성해야 하는 것이지, 이진 트리가 자동으로 만들어지는 것이 아니다 ! "
그러므로! 이 도구를 활용하여 이진 탐색트리를 구현 해보자 !
우선 헤더파일 선언부터 하자 !
BinarySearchTree.h
//
// BinarySearchTree.h
// BinarySearchTree
//
// Created by 서희찬 on 2021/04/17.
//
#ifndef BinarySearchTree_h
#define BinarySearchTree_h
#include "BinaryTree2.h"
typedef BTData BSTData;
//BST의 생성 및 초기화
void BSTMakeAndInit(BTreeNode ** pRoot);
// 노드에 저장된 데이터 반환
BSTData BSTGetNodeData(BTreeNode * bst);
// BST를 대상으로 데이터 저장(노드의 생성과정 포함)
void BSTInsert(BTreeNode ** pRoot, BSTData data);
// BST를 대상으로 데이터 탐색
BTreeNode * BSTSearch(BTreeNode * bst, BSTData target);
#endif /* BinarySearchTree_h */
이제 간단한 메인 함수를 보고 헤더파일에 선언된 함수들의 사용법을 알아보자 .

BTreeNode * bst = bstRoot
BTreeNode ** pRoot = &bstRoot
이진 탐색 트리의 구현 : 삽입과 삭제
삽입은 정말 말 그대로
"비교대상이 없을 때까지 내려간다"
"비교대상이 없는 그 위치가 새 데이터가 저장될 위치이다."
이다.
그림을 통해 예를 보자 !
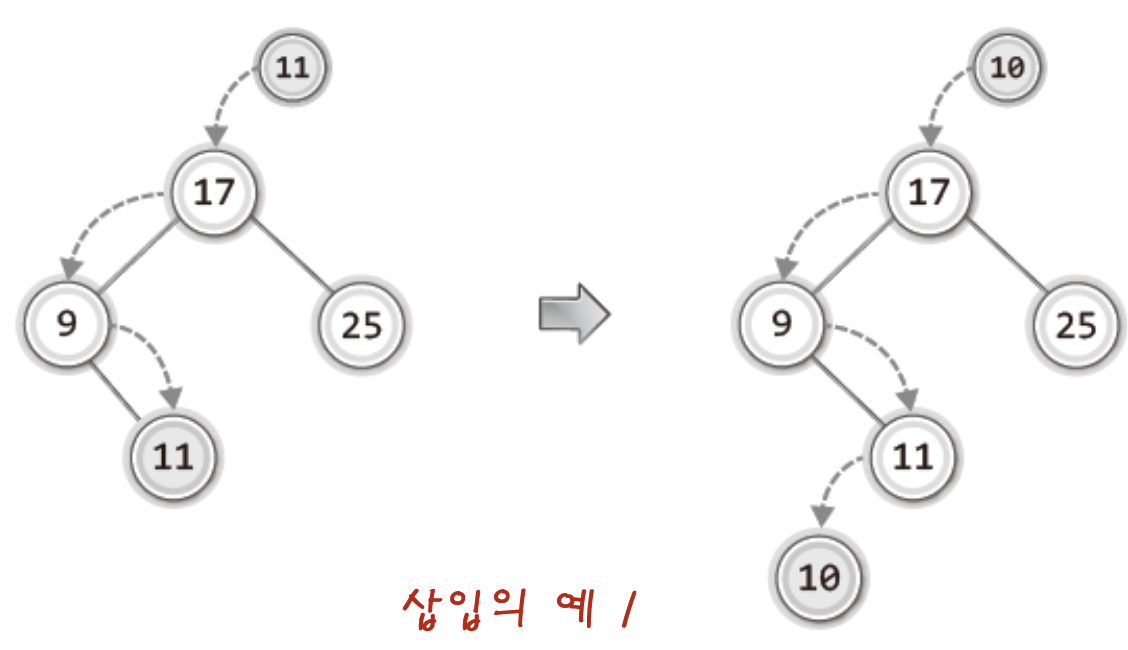
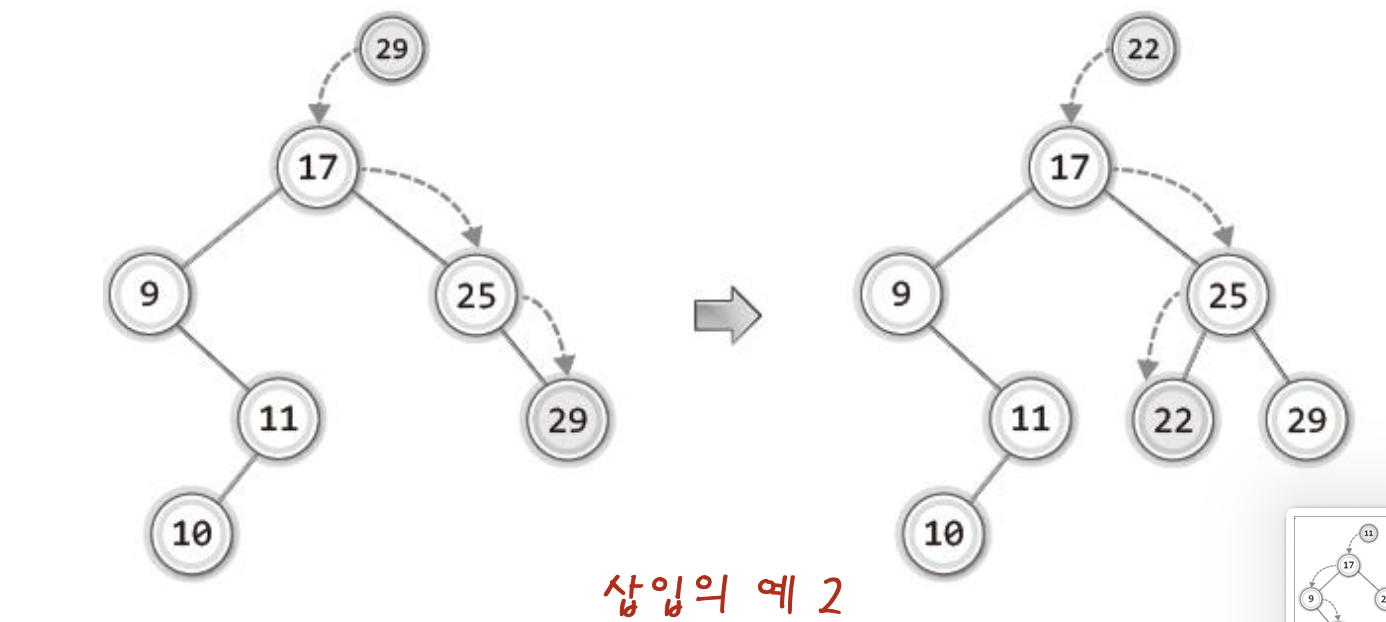
어떤가! 말 그대로이지 않는가!
이제 이를 그대로 코드로 옮겨보자 .
void BSTInsert(BTreeNode ** pRoot, BSTData data)
{
BTreeNode * pNode = NULL; //parent Node
BTreeNode * cNode = *pRoot; // Current Node
BTreeNode * nNode = NULL; // New Node
// 새노드 저장될 위치 찾는다.
while(cNode != NULL)
{
if(data == GetData(cNode))
return; // 데이터 중복 허용 x
pNode = cNode;
if(GetData(cNode)>data)
{
cNode = GetLeftSubTree(cNode);
}
else
cNode = GetRightSubTree(cNode);
}
//pNode의 자식 노드로 추가할 새 노드의 생성
nNode = MakeBTreeNode(); // 새 노드 생성
SetData(nNode, data);
// pNode 의 자식 노드로 추가할 새 노드의 생성
if(pNode != NULL) // 새 노드가 루트노드아니라면
{
if(data < GetData(pNode))
MakeLeftSubTree(pNode, nNode);
else
MakeRightSubTree(pNode, nNode);
}
else{ //새노드가 루트노라면
*pRoot = nNode;
}
}추가 설명을 하고 끝마치겠다.
먼저 while문을 보자.
이 while문은 저장할 값의 크기에 따라 왼/오로 이동하며 새 노드의 저장 위치를 찾는것이다.
따라서 이 while문이 끝나면
cNode에 저장될 위치정보가 담긴다.
그런데!!!!!
이 이취에 노드를 저장하기 위해 필요 한것은 바로!
이 위치를 자식으로 하는 부모 노드의 주소 값이다 !!
왜냐!?
부모 노드에 자식노드의 주소값이 저장 되기 때문이다!!
그래서 !
이후 부모 노드의 주소 값이 담긴 pNod를 기반으로 자식 노드를 추가 한다!!
그래서 while문을 통해 저장할 위치의 부모 노드를 pNode에 저장하고 탈출 한 후, nNode를 pNode의 데이터와 비교한 후 왼/오 중 한 곳에 저장한다.
이제 다음 포스트에서 탐색함수를 배워보자 !
