충돌 문제의 해결책
충돌문제해결이라는것은 생각외로 우리가 생각하는 수준에서 벗어나지 않는다!
충돌이 발생하면 그 자리를 대신할 자리를 찾는 방법을 찾는것이니깐 말이다!!
선형 조사법과 이차 조사법
선형 조사법
해쉬 함수 f(x)가 있고 테이블의 내부 저장소가 배열이라고 가정하면

이와 같다!
말그대로 선형적이며
충돌이 발생하면 충돌발생 다음자리에 저장하는것이다.
이 방법을 보면 척! 하고 문제가 있다는것을 알것이다.
바로 충돌이 발생하면 다음자리..다음자리.. 이렇게 저장하다보니 특정 영역에 데이터가 집중적으로 몰리는 현상인 "클러스터 현상"이 발생한다!!!!
이것이 단점이다!!
이것을 극복하기 위해
좀 멀리서 빈 공간을 찾을까?? 라는 생각에 탄생한 것이 이차 조사법이다.
이차 조사법
이차 조사법은 비슷하나 
n^2칸 옆의 슬롯을 검사한다!
즉 좀 더멀리서 빈 공간을 찾으려는 노력을 담았다.
그리고 앞선 코드를 구현할때 DELETED 상태가 불필요했지만 정의했다고 했는데
그 이유를 보여주겠다.
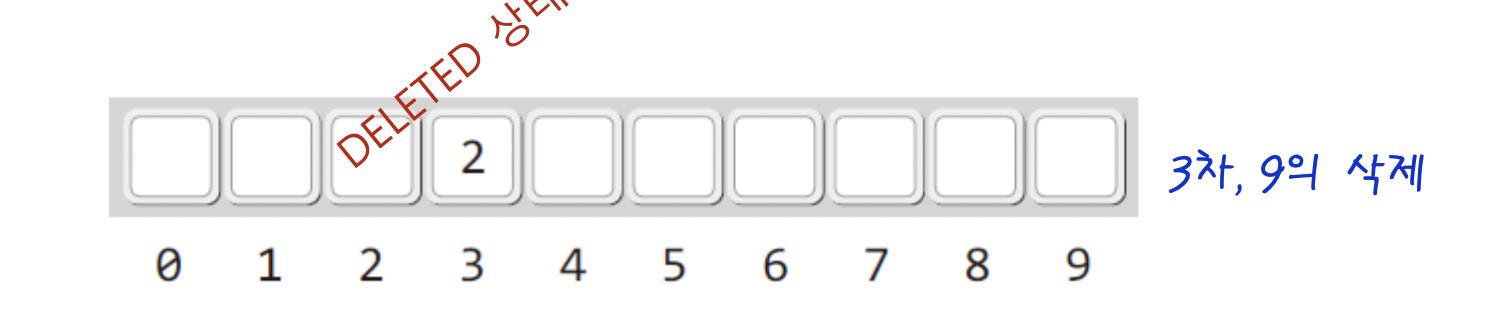
주목해야할점 삭제된 슬롯의 상태를 DELETED 로 두어서 EMPTY와 구분 하였다는것이다!
이렇게 구분하여 두어야 하는 이유는
키가 2인 데이터 탐색 과정을 살펴보면 알수 있다.
데이터 탐색을 위해 %7인 해쉬 함수를 거치는데 그 결과로 얻은 2를 인덱스 값으로 하여 탐색을 진행하는데 만약 슬롯 상태가 EMPTY 라면 데이터가 존재하지 않는다고 판단하여 탐색을 종료한다!
이렇게 되면 그 옆자리도 확인하지않고 종료한다는말이다!!
무엇이 문제인지 알겠는가?
좀 더 상세히 말하자면 충돌이 발생하면 옆자리에 저장 되는데
만약 DELETED 대신 EMPTY 상태라면 그 옆자리를 확인하지 않고 탐색을 종료하여 충돌이 발생하여 다른 자리에 저장된 동일한 키 값을 가진 요소를 확인하지 못한다는 점이다.
즉, DELTED 상태라면 충돌이 발생했음을 의심하여 선형,이차조사법에 근거한 탐색의 과정을 진행해야한다 !
이렇듯 DELTED 상태는 충돌의 해결책과 관련이 있다 !
이중해쉬
이차조사법에도 물론 문제가 있다.
바로
"해쉬 값이 같으면 충돌 발생시 빈 슬롯을 찾기 위해서 접근하는 위치가 늘 동일하다."
당연하다!
우리는 해시함수를 기준으로
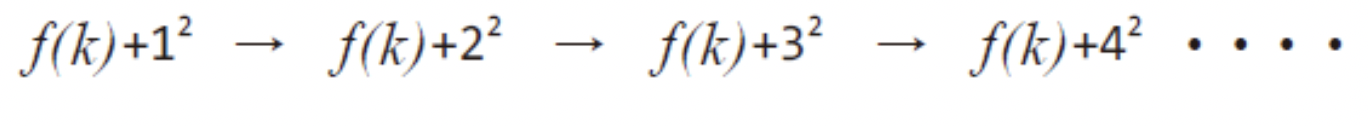
이 순서대로 일정하게 빈 슬릇을 찾게될것이다.
이렇듯 해쉬 값이 같을 경우 선형 조사법보단 낫지만 접근하는 위치가 동일하여 여전히~ 클러스터 현상이 발생활 확률이 높다.
이러한 단점을 어떻게 해결할까?
생각해보자!
규칙적인게 문제라고 하지 않았는가?
그렇다면 불규칙적으로 구성된다면 되지 않겠는가?
정답이다!!!!
이렇한 생각이 반영된것이
이중해쉬 방법이다!
이는 두 개의 해쉬 함수를 이용하기 때문에 붙여진 이름이다.
하나는 앞서 보인 것과 마찬가지로 키를 근거로 저장위치를 결정하고!
반면 다른 하나는 충돌이 발생했을 때, 몇 칸 뒤에 위치한 슬롯을 살펴볼지 그 거리를 결정하기 위한 것이다.
- 1차 해쉬 함수 : 키를 근거로 저장위치를 결정하기 위한 것
- 2차 해쉬 함수 : 충돌 발생시 몇 칸 뒤를 살필지 결정하기 위한 것
그럼 함수를 보자 !

위 함수식은 절대적인 것은 아니지만 일반적인 형태라고 볼 수있다!
%15를 보아 배열의 길이가 15인것을 눈치 챌 수 있다.
c같은 경우는 15보다 작은 소수중 하나로 결정하면 된다.
2차 해쉬 함수를 좀 더 자세히 보자 .
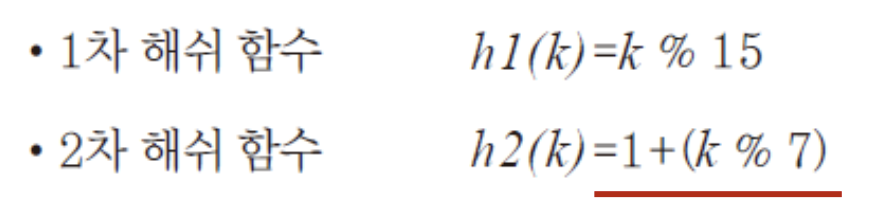
- 1을 더하는 이유 : 2 차 해쉬 값이 0이 되는것을 방지하기 위해서
- c를 15보다 작은 값으로 하는 이유 : 배열의 길이에 맞춘것(만약 배열의 길이보다 크면 몇바퀴 돌수도 있다!)
- c를 소수로 결정하는 이유 : 클러스터 현상을 낮춘다는 통계가 있다 !!

이렇듯 충돌이 발생한 두개의 키를 대상으로 2 차 해쉬 값을 계싼 해보면 다르다!!!
그리고 이 2차 해쉬 값을 근거로 빈 슬롯을 찾는 과정은

이와 같다!!!
이렇듯 2차 해쉬 값의 크기만큼 건너 뛰면서 빈 슬롯을 찾게 되므로
키가 다르면 건너 뛰는 길이도 달라져 클러스터 현상의 발생 확률을 현저히 낮출 수 있다.
참고로 실제도로 이중 해쉬는 이상적인 충돌 해결책으로 알려져 있다.
