Metric + Collaborative filtering
이 논문의 재미있는 점은 item끼리 직접적으로 loss function은 없고 user - item이 가까워지게 함으로써 item끼리도 가까워지게 한다는 것!
Introduction
"x is similar to both y and z"는 두 페어를 가깝게하는 것뿐만 아니라 (y, z) 역시 가깝게 만든다 ! 이를 similarity propagtion이라고 한다.
learned metric의 시각화를 통해서 user의 선호도를 표현할 수 있음
Matrix Factorization의 경우 dot product를 수행하기 때문에 triangle inequality 만족X
=> 이유는 user-item의 관계가 item-item까지 전파되지 않았기 때문
논문 모델의 목표
data point x가 있을 때 target neighbor들이 가까워지게 하는 것
general하게는 imposter의 수를 줄이는 것!
Collaborative Metric Learning(CML)
metric이 비슷한 Set의 Pair들을 가깝게 하고, 다른 pair들은 멀어지게 함
-> 결과적으로 같은 item을 좋아한 user들은 가까워지고, 같은 user가 좋아하는 item 역시도 가까워짐
따라서 nearest neighbor item은 어떤 user가 주어졌을 때,
해당 user가 이전에 좋아했던 item들 + user와 비슷한 다른 user가 좋아한 item들즉, user-item 관계만 포함하는 게 아니라 user-user, item-item 관계도 표현할 수 있음
Model Formulation
Euclidean distance
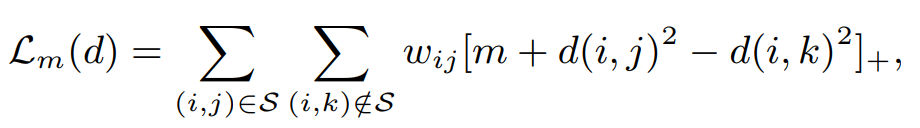
LMNN과의 차이
- L_pull이 없고
- user의 traget neighbor만 고려함
- weighted ranking loss
흥미로운점
Positive item을 단순히 pull하는 loss보다는 rank에 기반하여 penalize함 (+ user만 고려해도 item도 같이 됨!)
Approximated Ranking Weight
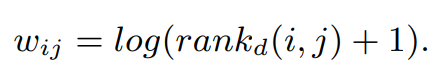
positive인데 rank 낮을수록 가중치 더 크게 penalize
rank를 gradient descent마다 계산하는 건 비싸니까 sampling을 반복해서 시간 복잡도를 줄임..