
DFS, BFS모두 정점 node와 그 node들을 연결하는 간선 edge로 이루어진 그래프를 탐색할 때 사용하는 방법이다.
❗️여기서 그래프를 탐색한다 ❗️ 라는 말은
한 정점으로부터 시작해서 모든 정점을 한 번씩 방문하는 것을 말한다.
✨ 너비 우선 탐색 (BFS, Breadth-First Search)
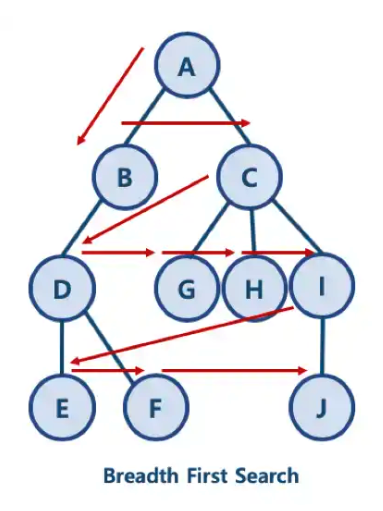
방문하지 않은 최상단 노드에서 인접한 노드를 먼저 모두 탐색하고, 이후 다음 자식 노드로 이동하는 방법이다.
주로 두개의 노드 사이에서의 최단 경로를 찾고 싶을 때 적절한 탐색방법이며, 두 개의 큐를 사용하여 구현한다.
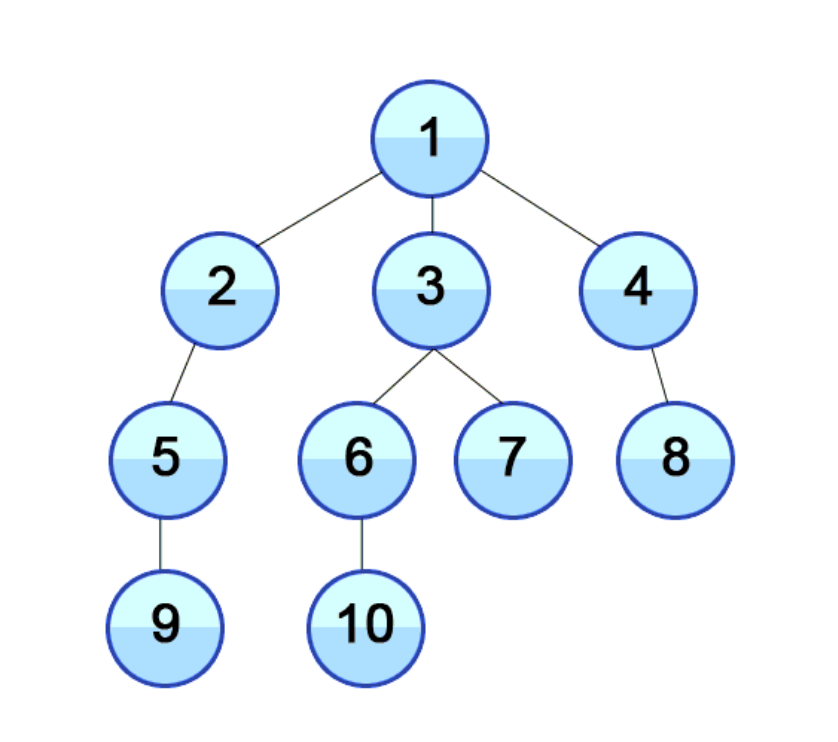
해당 그림을 보면 최상단의 자식 노드들 중에서 왼쪽 노드부터 너비 탐색을 진행하고, 해당 자식들의 노드를 모두 탐색하면, 그 자식들의 자식 노드들로 이동한다.
JavaScript 코드
const graph = {
A: ["B", "C"],
B: ["A", "D"],
C: ["A", "G", "H", "I"],
D: ["B", "E", "F"],
E: ["D"],
F: ["D"],
G: ["C"],
H: ["C"],
I: ["C", "J"],
J: ["I"]
};
const BFS = (graph, startNode) => {
const visited = []; // 탐색을 마친 노드들
let needVisit = []; // 탐색해야할 노드들
needVisit.push(startNode); // 노드 탐색 시작
while (needVisit.length !== 0) { // 탐색해야할 노드가 남아있다면
const node = needVisit.shift(); // queue이기 때문에 선입선출, shift()를 사용한다.
if (!visited.includes(node)) { // 해당 노드가 탐색된 적 없다면
visited.push(node);
needVisit = [...needVisit, ...graph[node]];
}
}
return visited;
};
console.log(BFS(graph, "A"));
// ["A", "B", "C", "D", "G", "H", "I", "E", "F", "J"]✨ 깊이 우선 탐색 (DFS, Depth-First Search)
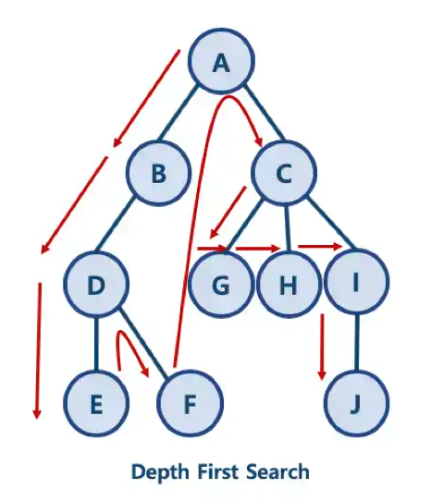
최대한 하단 노드로 내려가면서, 더이상 자식이 없을경우에 방문하지 않은 노드중 최상단의 노드로 다시 올라간다.
주로 경로의 존재 여부를 판단하고자 하는 상황일때 적절한 탐색 방법이며, 한 개의 큐, 한 개의 스택을 사용한다.
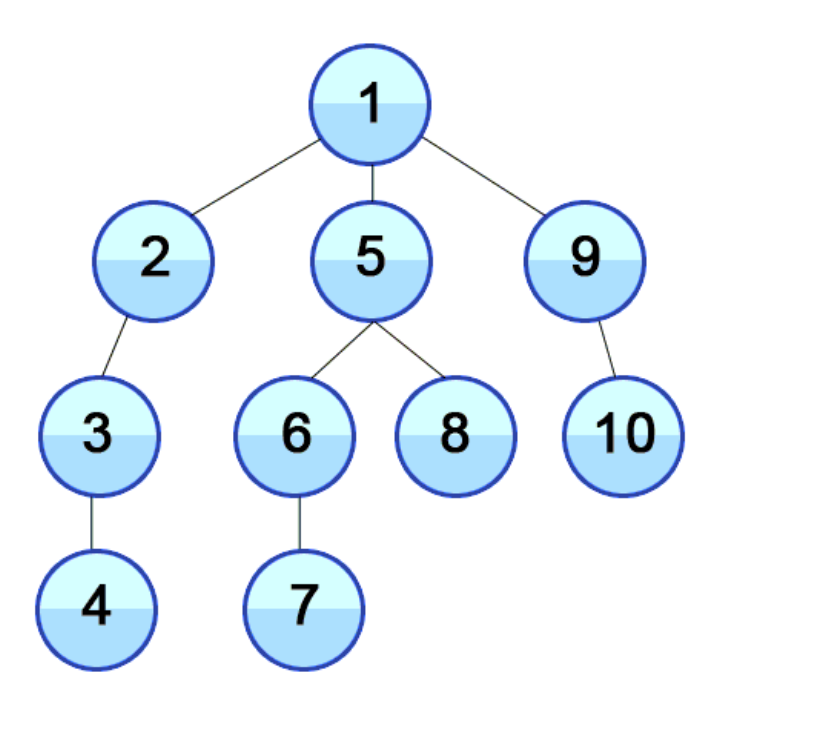
해당 그림을 보면 최상단 노드의 제일 왼쪽 자식 노드들부터 깊이 탐색을 차례대로 진행한다.
JavaScript 코드
const graph = {
A: ["B", "C"],
B: ["A", "D"],
C: ["A", "G", "H", "I"],
D: ["B", "E", "F"],
E: ["D"],
F: ["D"],
G: ["C"],
H: ["C"],
I: ["C", "J"],
J: ["I"]
};
const DFS = (graph, startNode) => {
const visited = []; // 탐색을 마친 노드들
let needVisit = []; // 탐색해야할 노드들
needVisit.push(startNode); // 노드 탐색 시작
while (needVisit.length !== 0) { // 탐색해야할 노드가 남아있다면
const node = needVisit.shift(); // queue이기 때문에 선입선출, shift()를 사용한다.
if (!visited.includes(node)) { // 해당 노드가 탐색된 적 없다면
visited.push(node);
needVisit = [...graph[node], ...needVisit];
}
}
return visited;
};
console.log(DFS(graph, "A"));
// ["A", "B", "D", "E", "F", "C", "G", "H", "I", "J"]정리를 하면 다음과 같다
| BFS | DFS |
|---|---|
| 현재 정점에서 연결된 인접한 노드들 부터 탐색 | 현재 정점에서 갈 수 있는 자식 노드까지 밑으로 들어가면서 탐색 |
| 큐를 이용해 구현 | 스택 또는 재귀함수로 구현 |
✨ 문제 유형
-
그래프의
모든 정점을 방문하는 것이 중요한 문제
DFS, BFS 어느것도 괜찮다 -
경로의 특징을 저장해두어야 하는 문제
DFS를 사용해야 경로 저장이 가능하다 -
최단 거리를 구해야 하는 문제
BFS로 탐색해야 한다 -
그외
검색 대상 그래프의 범위가 너무 큰 경우 -> DFS
규모는 크지 않으며, 검색 시작 노드로부터 목표 노드까지의 거리가 멀리 않은 경우 -> BFS
✨ 시간 복잡도
DFS, BFS 모두 노드 수와 간선 수를 더한 복잡도인 O(n)을 가진다.
📚 학습할 때, 참고한 자료 📚
