그래프
벨만-포드
가중 그래프에서 단일 쌍, 단일 출발, 단일 도착 최단 경로 문제를 구할 때 사용
📍특징
- 음의 가중치를 가지는 간선도 가능
- 음의 사이클의 존재 여부를 확인할 수 있음 -> 음의 사이클이 있다 = 현재 그래프에서 최단 거리를 찾을 수 없다 => 탐색 종료!!
- 최단거리를 구하기 위해서 V-1번씩 E개의 모든 간선을 확인함
- 음의 사이클 존재 여부를 확인하기 위해 한번 더 E개의 간선을 확인
- 총 연산횟수는 V*E 즉, O(VE)
- V번째 간선을 확인하고 거리배열이 갱신되었다면 그래프 G는 음의 사이클을 가지는 그래프이다.
💡수행 과정
벨만-포드 진행과정은 다음과 같다.-
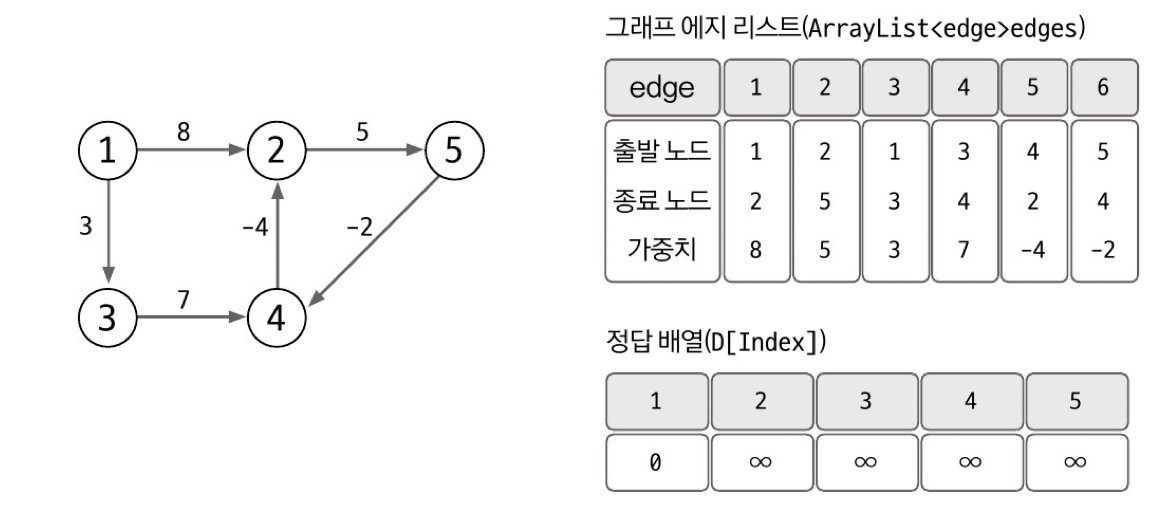
에지 리스트로 그래프를 구현하고 최단 경로 배열 초기화하기
- 간선을 중심으로 동작하므로 간선 리스트를 구현해야 한다.
- 최단 경로 배열은 출발 노드를 0, 나머지 노드를 무한대로 초기화한다.
-
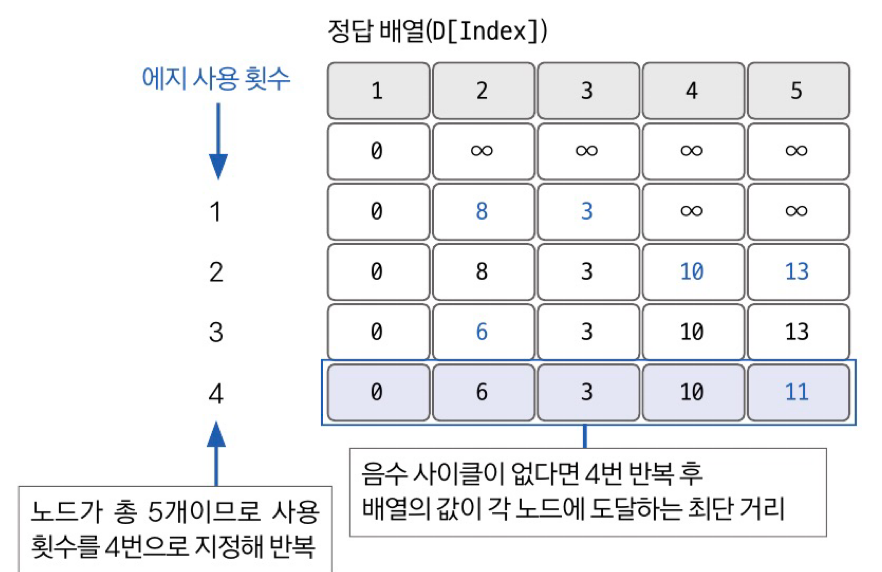
모든 에지를 확인해 정답 배열 업데이트하기
-
최단 거리 배열에서 업데이트 반복 횟수는 V-1번이며
-
음수 사이클 확인을 위해 위 과정을 한 번 더 확인하므로
-
시간 복잡도는 O(VE)가 됨!
-
-
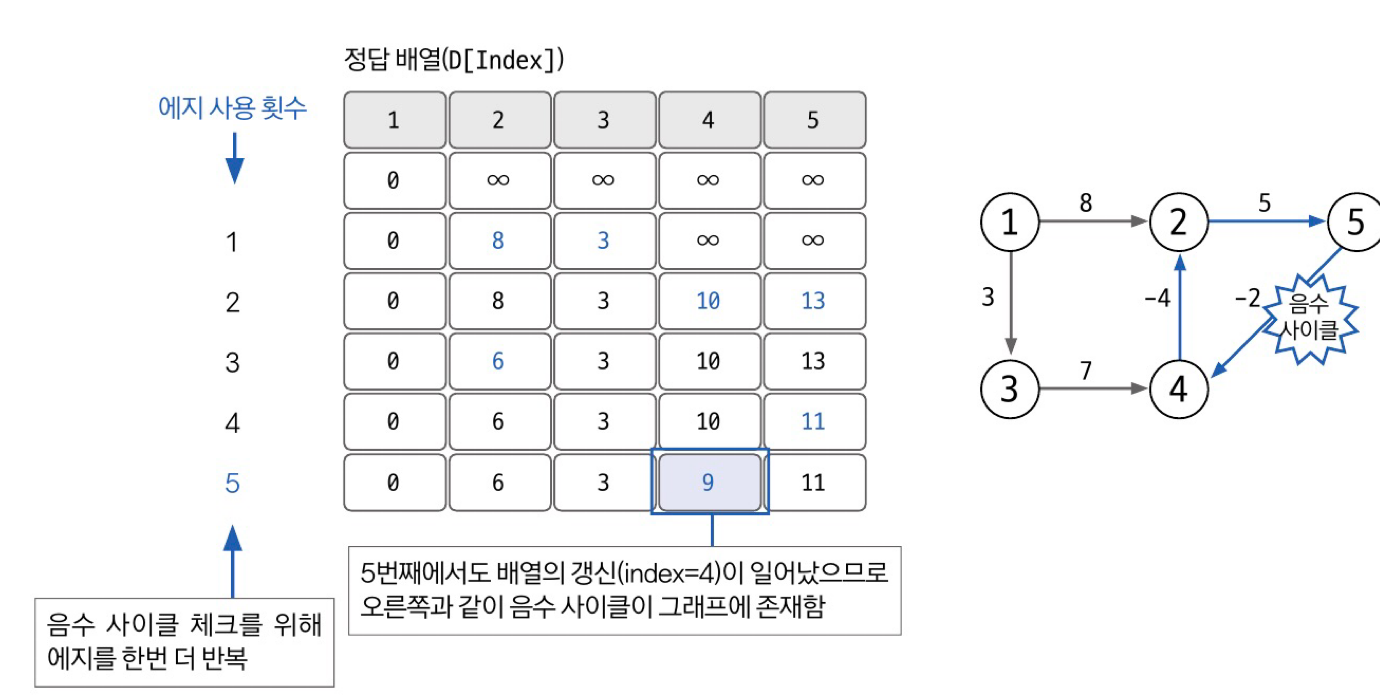
음수 사이클 유무 확인하기
-
모든 에지를 돌면서 최단거리배열에 업데이트가 발생하는지 확인한다.
-
업데이트 되는 노드가 있다 = 음수 사이클이 있다
=> 최단거리배열이 무의미하고 그래프는 최단 거리를 찾을 수 없다는 의미가 됨 !
-
플로이드-워셜
전체 쌍 최단 경로 문제 _ DP로 접근하자!
📍특징
- 순환만 없다면 음수 가중치도 가능
- 모든 가능한 경유지에 대해서 모든 정점에서 모든 정점으로 가는 최단거리를 확인하므로 시간 복잡도는 O(V^3)
✔️A 노드에서 B 노드까지 최단 경로를 구했다고 가정했을 때
최단 경로 위에 K가 존재한다면 그것을 이루는 부분경로 역시 최단 경로라는 의미
✔️최단경로는 A-B이거나 A-K-B이다. 💡수행 과정
플로이드-워셜 진행과정은 다음과 같다.- 배열 선언하고 초기화하기(인접행렬)
- D[s][e]는 노드 S에서 E까지의 최단거리를 저장하는 배열
- if(s == e) D[s][e] =0; else D[s][e] = INF
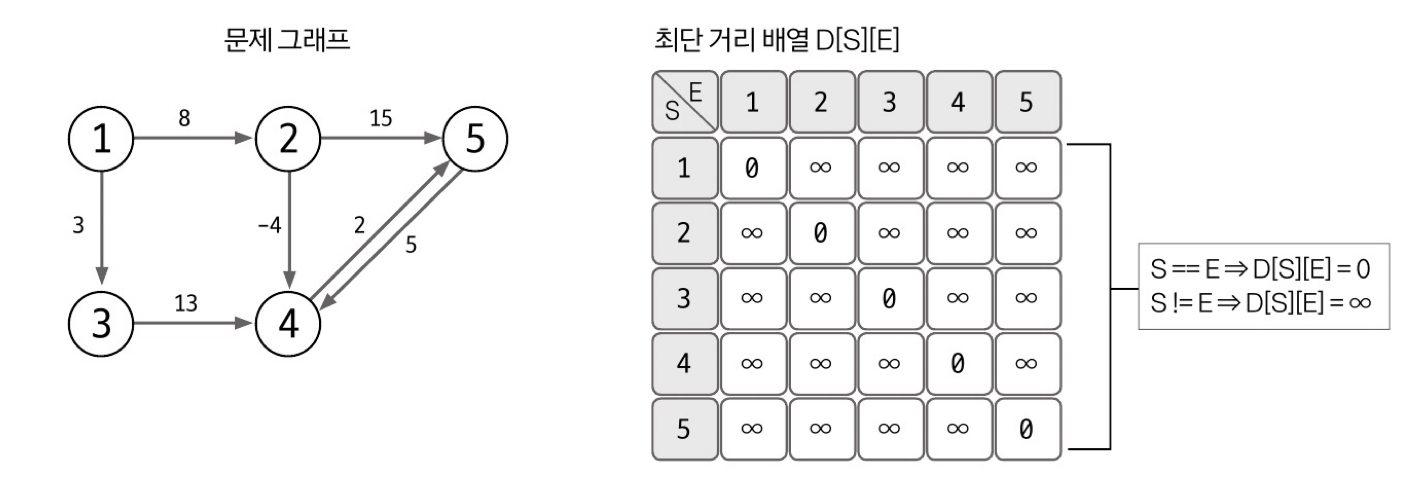
- 최단 거리 배열에 그래프 데이터 저장하기
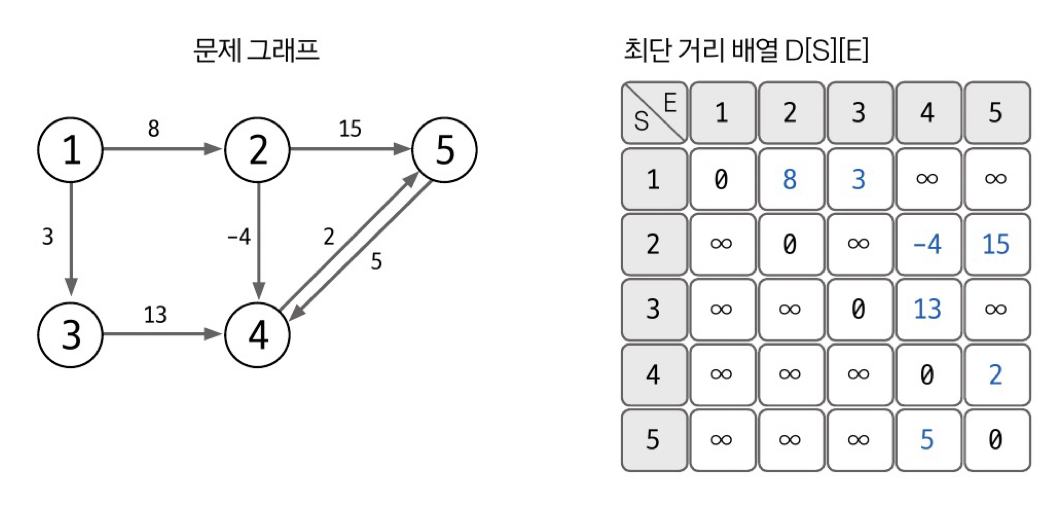
- 배열 업데이트하기
for 경유지 K에 대해 (1~N)
for 출발노드 S에 대해(1~N)
for 도착노드 E에 대해(1~N)
D[s][e] = Math.min(D[s][e], D[s][k]+D[k][e])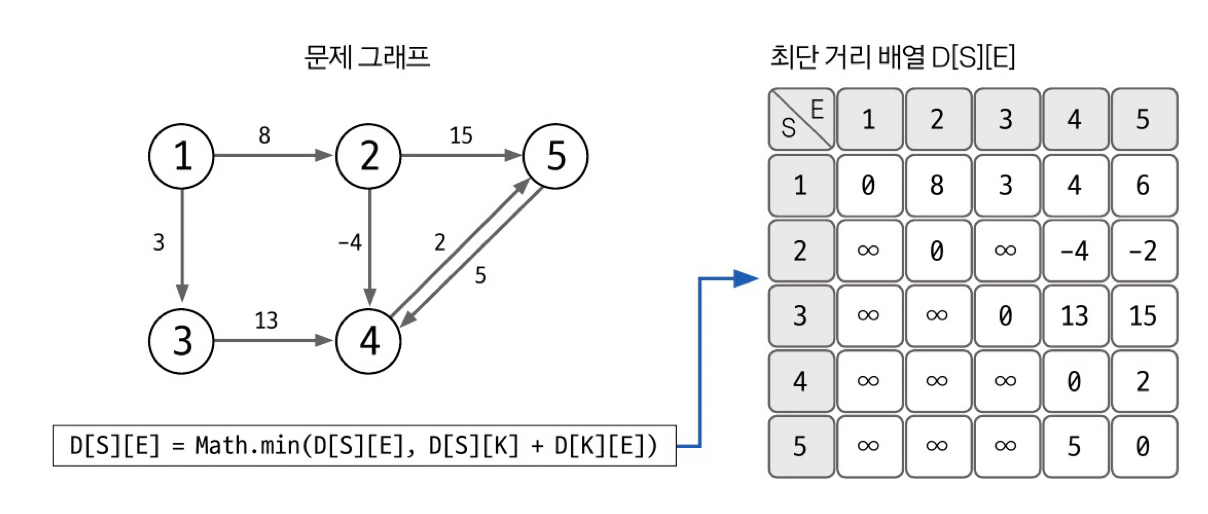
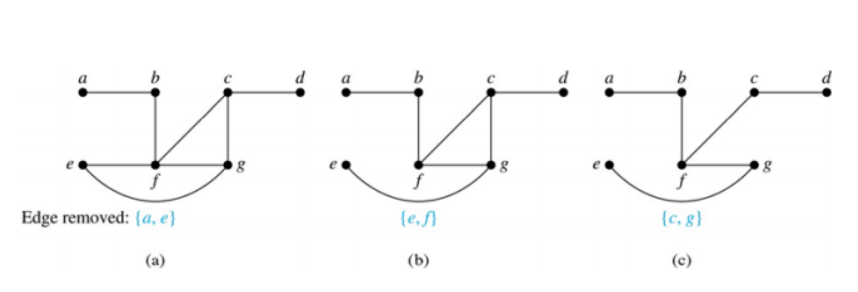
신장 트리(Spanning tree)
연결 그래프이며, G의 모든 정점을 포함하고 있는 트리구조.
트리의 종류는 하나가 아니다.
ex)
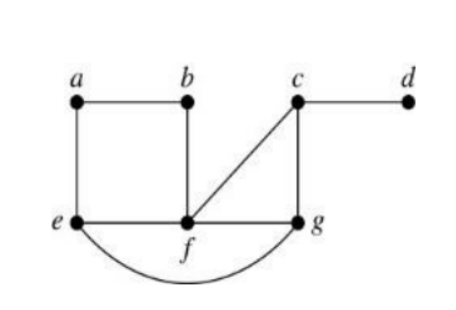
💡 신장 트리로 만들기 위해서는 모든 순회를 없애야 한다.
최소 신장 트리
무향 연결 가중 그래프G에서 간선의 가중치의 합이 최소인 신장 트리 -> 그리디 알고리즘!
📍특징
- 사이클이 포함되면 가중치의 합이 최소가 될 수 없으므로 사이클을 포함 x -> union-find로 사이클 형성 확인함
- N개의 노드가 있으면 MST를 구성하는 에지의 개수는 항상
N-1개- 문제 유형은 다음과 같다.
- 여러 개의 네트워크 지점들이 있는데,
모든지점들을 유선으로 연결하되연결선의 총 길이가 최소가 되야 하는 문제- 도시들을
모두연결하되, 연결하는도로의 길이 합이 최소가 되야 하는 문제
💡핵심 이론
-
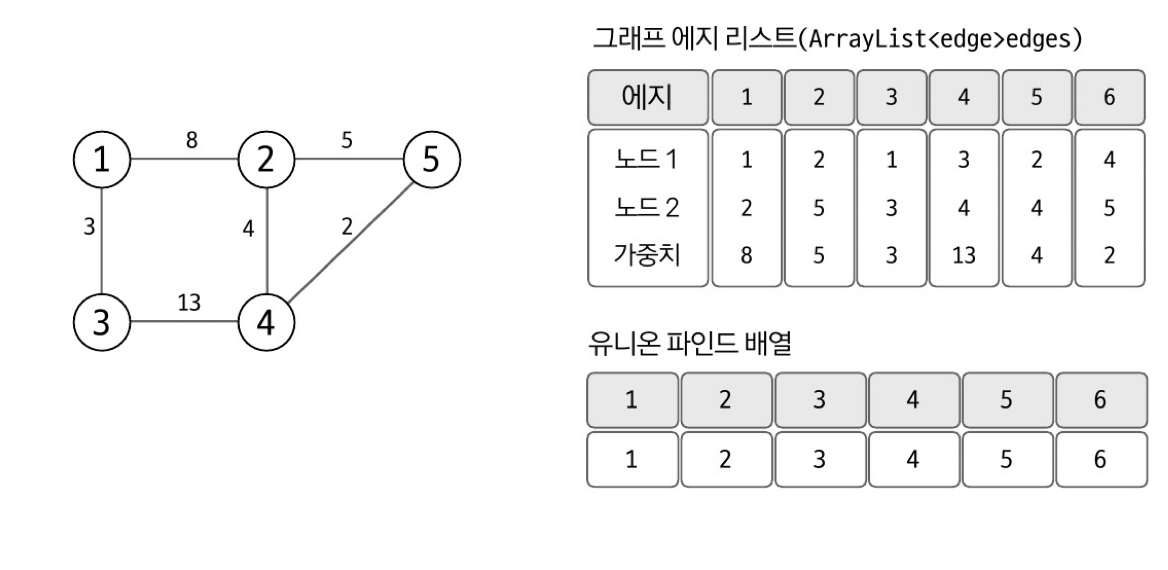
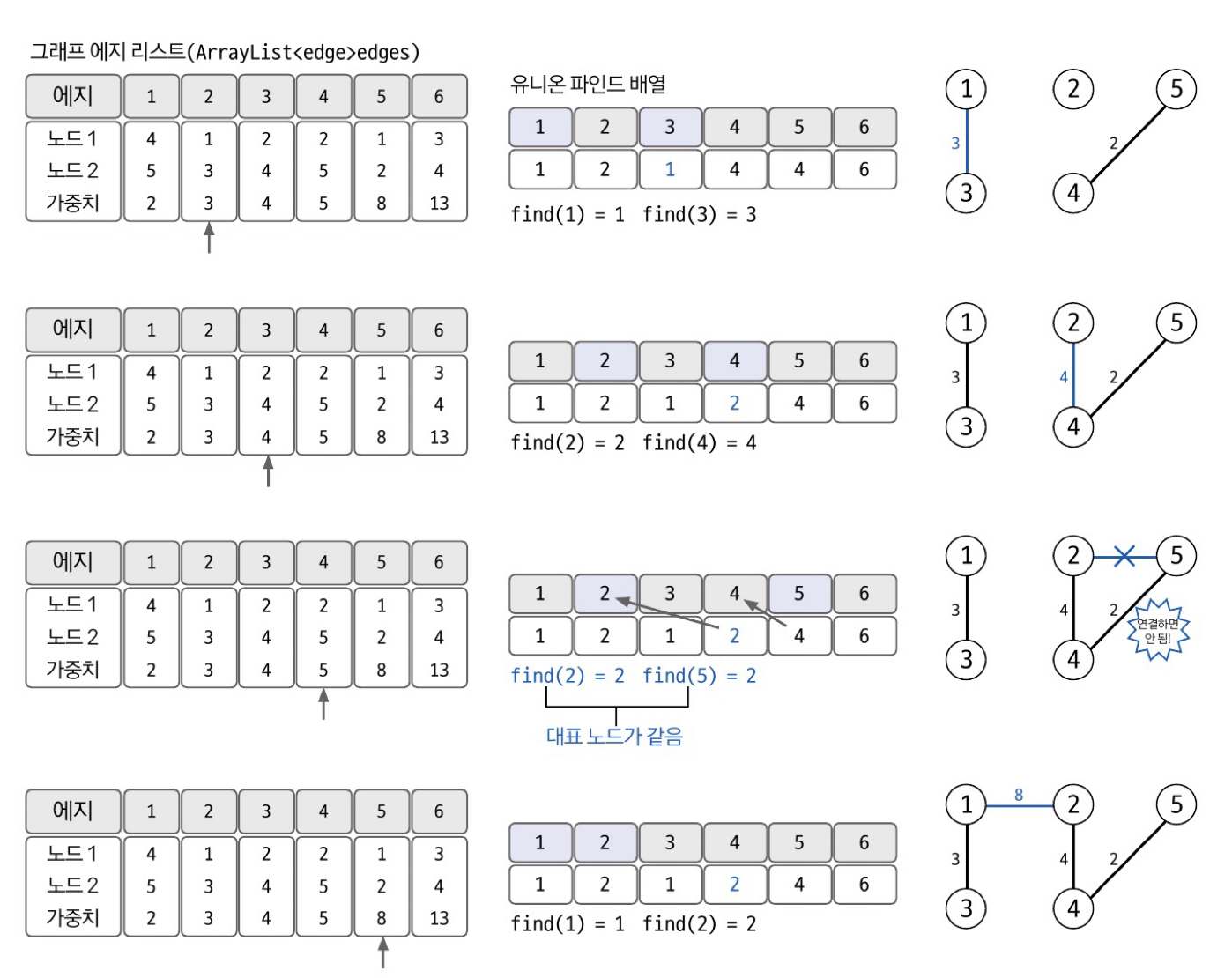
에지 리스트로 그래프를 구현하고 union-find 배열 초기화하기
- 데이터는 에지를 중심으로 저장되므로 에지 리스트의 형태로 저장한다.
- 사이클 처리를 위해 union-find 배열도 함께 초기화함
배열의 인덱스를 해당 자리의 값으로 초기화
-
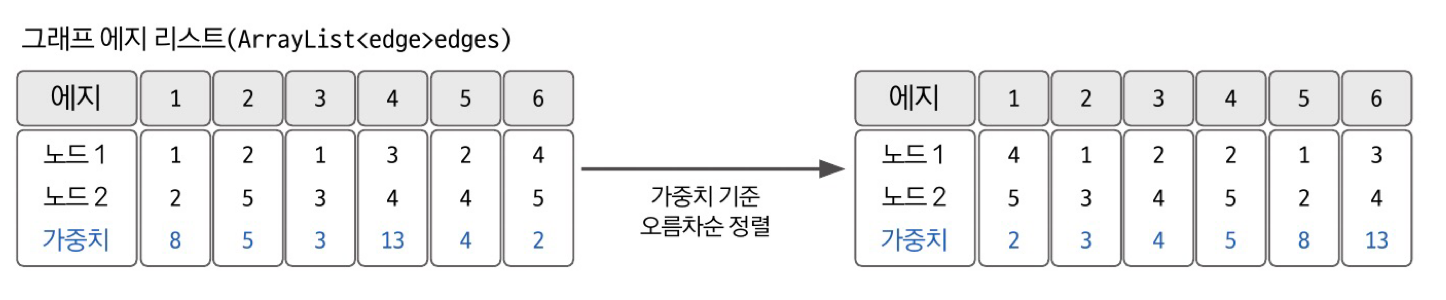
그래프 데이터를 가중치 기준으로 정렬
-
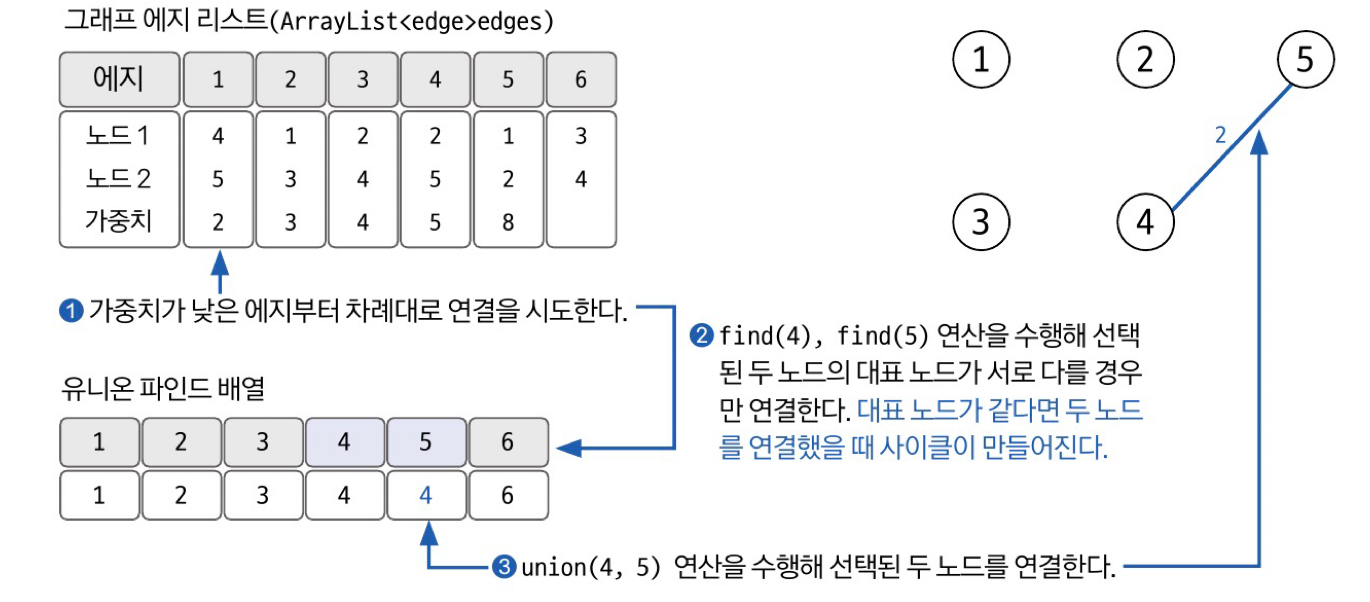
가중치가 낮은 에지부터 연결 시도하기
- 바로 연결하지 않고 이 에지를 연결했을 때 그래프에 사이클이 형성되는지를 find 연산을 통해 확인한 후 사이클 형성 안되면 union 연산 수행함
-
연결한 에지의 개수가 N-1개일때까지 3번 반복!
-
총 에지 비용 출력
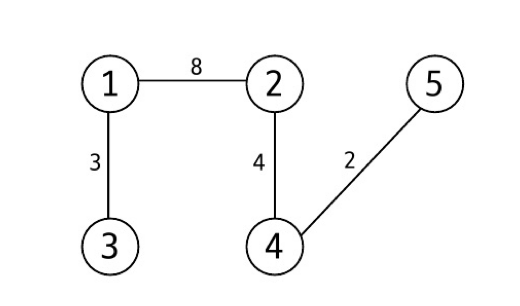
크루스칼 알고리즘(간선 중심 알고리즘)
- 그래프 간선을 가중치 오름차순으로 정렬함
- 사이클을 형성하지 않는 선에서 정렬된 순서대로 간선을 선택함
- 사이클이 생겼는지 확인할 땐 union&find를 활용하자 !
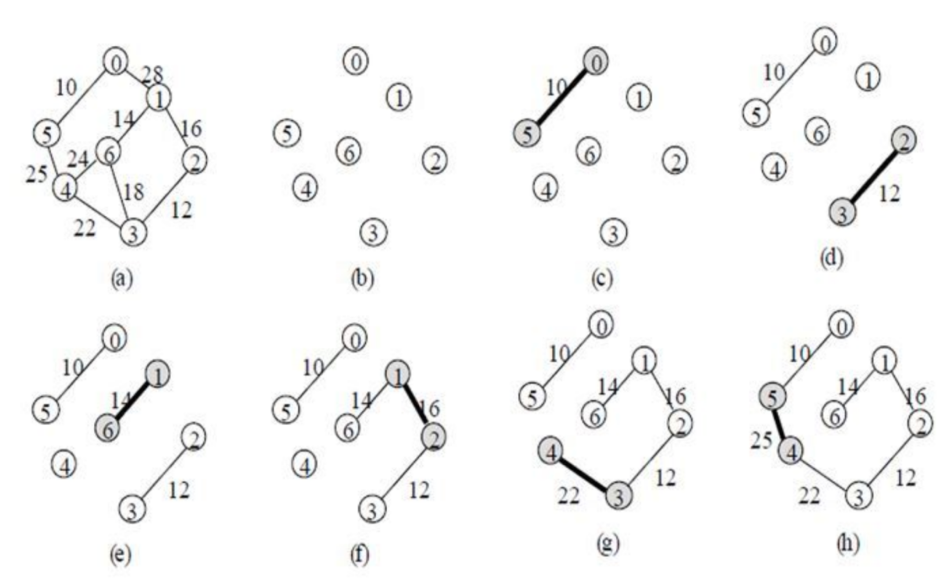
1. 모든 간선들의 가중치를 오름차순으로 정렬

2. 가중치가 가장 작은 간선을 순서대로 선택하고 연결
2번 과정에서 사이클이 발생했을 시엔 포함을 하지 않는다

💡code
class Node implements Comparable<Node>{
int to;
int from;
int value;
public Node(int to, int from, int value) {
this.to = to;
this.from = from;
this.value = value;
}
@Override
public int compareTo(Node o) {
return this.value - o.value;
}
}
public class Main {
private static int n;
private static int[] parents;
public static void main(String[] args) {
n = 7;
int[][] graph = {{1,2,29}, {1,5,75},{2,3,35},{2,6,34}, {3,4,7},{4,6,23},
{4,7,13}, {5,6,53}, {6,7,25}};
parents = new int[n + 1];
for (int i=1; i<n+1; i++) {
parents[i] = i;
}
Queue<Node> pq = new PriorityQueue<>();
for(int i=0; i<graph.length; i++) {
int to = graph[i][0];
int from = graph[i][1];
int value = graph[i][2];
// 우선순위 큐는 자동으로 간선 비용순(오름차순)으로 정렬된다.
pq.add(new Node(to, from, value));
}
int size = pq.size();
int total =0;
// 간선 하나씩 조회 (비용이 작은 간선부터)
for(int i=0; i< size; i++) {
Node node = pq.poll();
int rx = find(node.to);
int ry = find(node.from);
// 사이클이 발생하지 않는 경우에만 집합에 포함
if(!isSameParent(rx, ry)) {
total += node.value;
union(node.to,node.from);
}
}
System.out.println(total);
}
static int find(int x) {
if (parents[x] == x) {
return x;
}
return parents[x] = find(parents[x]);
}
static void union(int x, int y) {
x = find(x);
y = find(y);
// 더 find 값으로 부모 노드 설정
if (x < y) {
parents[y] = x;
}
else {
parents[x] = y;
}
}
static boolean isSameParent(int x, int y) {
if(rx == ry) return true;
return false;
}
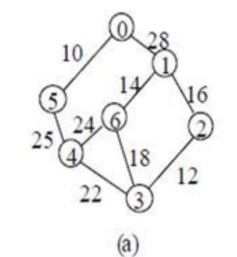
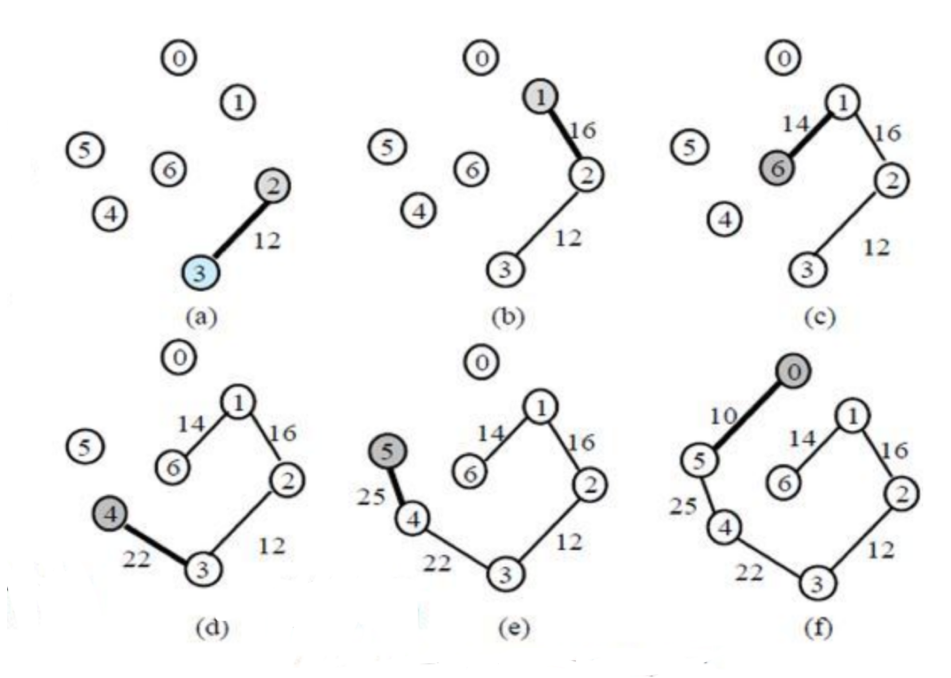
}프림 알고리즘(정점 중심 알고리즘)
- 그래프를 인접행렬로 구현함.
- 임의의 점을 하나 잡아 루트 노드로 시작하고, 주변 간선 중 최소 가중치를 갖는 간선을 선택함.
✔️우선순위큐로 구현하자 !
- 임의의 간선을 선택
- 선택한 간선의 정점으로부터 가장 낮은 가중치를 갖는 정점을 선택
모든 정점이 선택될 때까지 반복
💡code
class Node implements Comparable<Node>{
int to;
int value;
public Node(int to, int value) {
this.to = to;
this.value = value;
}
@Override
public int compareTo(Node o) {
return this.value - o.value;
}
}
public class Main {
static int total;
static List<Node>[] list;
static boolean[] visited;
public static void main(String[] args){
int v = 7;
int[][] graph = {{1,2,29}, {1,5,75},{2,3,35},{2,6,34}, {3,4,7},{4,6,23},
{4,7,13}, {5,6,53}, {6,7,25}};
list = new ArrayList[v+1];
visited = new boolean[v+1];
for(int i=1; i<v+1; i++) {
list[i] = new ArrayList<>();
}
for(int i=0; i<graph.length; i++) {
int a = graph[i][0];
int b = graph[i][1];
int w = graph[i][2];
list[a].add(new Node(b,w));
list[b].add(new Node(a,w));
}
prim(1);
System.out.println(total);
}
static void prim(int start) {
Queue<Node> pq = new PriorityQueue<>();
pq.add(new Node(start,0));
while(!pq.isEmpty()) {
Node p = pq.poll();
int node = p.to;
int weight = p.value;
if(visited[node]) continue;
// 선택한 간선의 정점으로부터 가장 낮은 가중치 갖는 정점 선택
visited[node]= true;
total += weight;
for(Node next : list[node]) {
if(!visited[next.to]) {
pq.add(next);
}
}
}
}
}- 프림은 시작점을 정하고, 시작점에서 가까운 정점을 선택하면서 트리르 구성 하므로 그 과정에서 사이클을 이루지 않지만 크루스칼은 시작점을 따로 정하지 않고 최소 비용의 간선을 차례로 대입하면서 트리를 구성하기 때문에 사이클이 이루어지는 항상 확인해야한다.
- 간선의 개수가 작은 경우에는 크루스칼, 간선의 개수가 많은 경우에는 프림.
