탐색(DFS&BFS)

📌 그래프를 탐색하는 방법에는 크게 깊이 우선 탐색(DFS)와 너비 우선 탐색(BFS)가 있다.

• 그래프를 탐색한다 → 하나의 정점으로부터 시작하여 주어진 모든 정점들을 차례대로 한 번씩 방문한다는 뜻!

DFS(깊이 우선 탐색)

재귀 함수로 구현하거나 스택을 이용함 !! → 시간복잡도는 O(V+E) // V: 노드 수, E: 에지 수

• 그래프 완전 탐색 기법 중 하나로, 그래프의 시작 노드에서 출발하여 탐색할 한 쪽 분기를 정하여 최대 깊이까지 탐색을 마친 후 다른 쪽 분기로 이동하여 다시 탐색을 수행함
• 재귀로 구현할 경우 스택 오버플로우에 유의해야 한다.
• DFS 활용 예로는 단절점 찾기, 단절선 찾기, 사이클 찾기, 위상정렬 등이 있다.

핵심 이론

📌한 번 방문한 노드 재방문 불가 → 방문 체크 배열 필요
📌최대한 깊이 내려간 뒤, 더이상 갈 곳이 없는 경우 옆으로 이동함

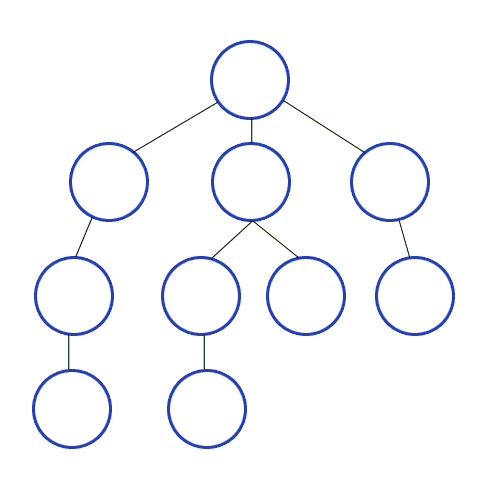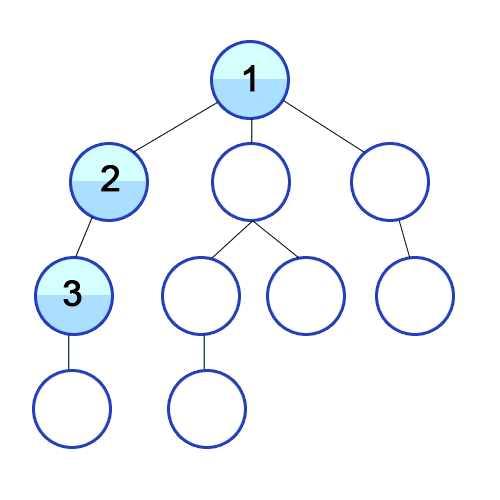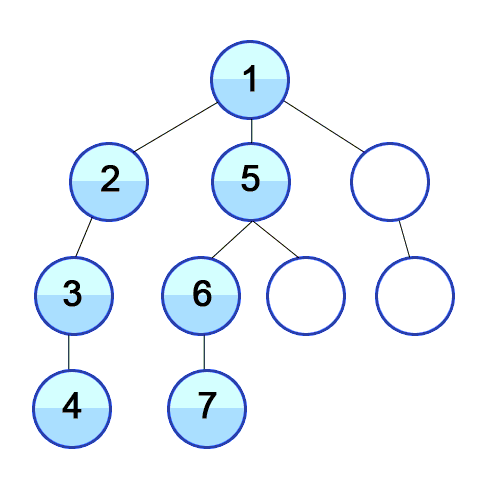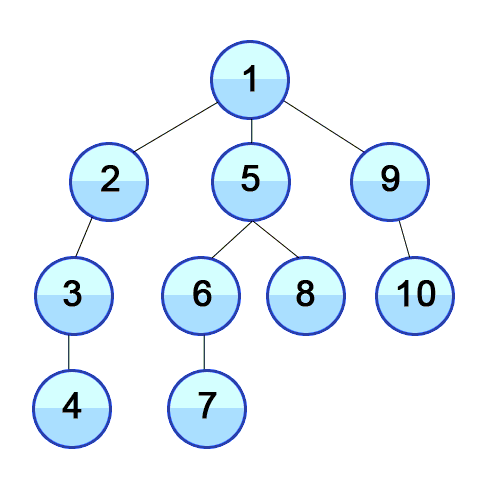
스택을 통한 구현 원리

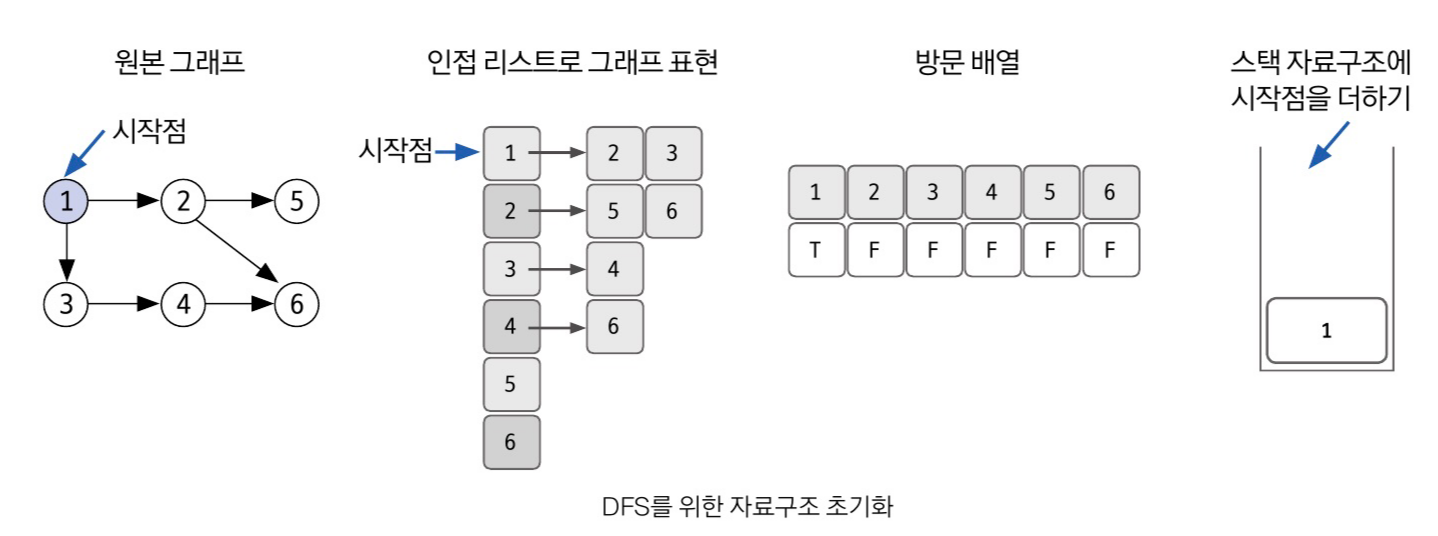
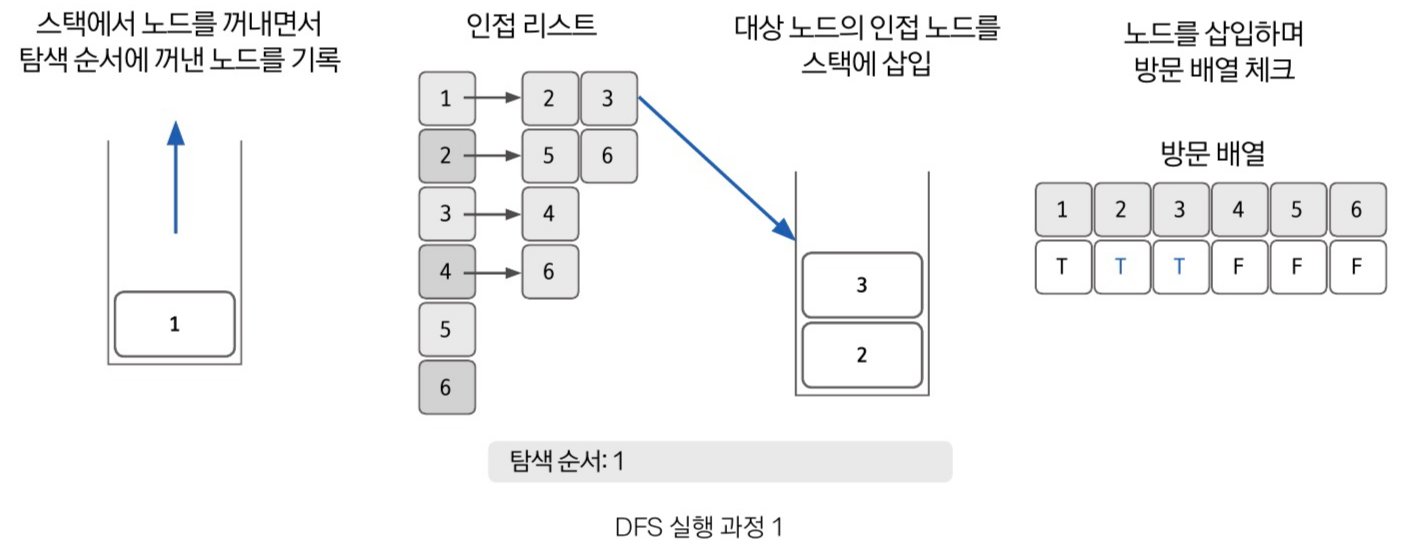
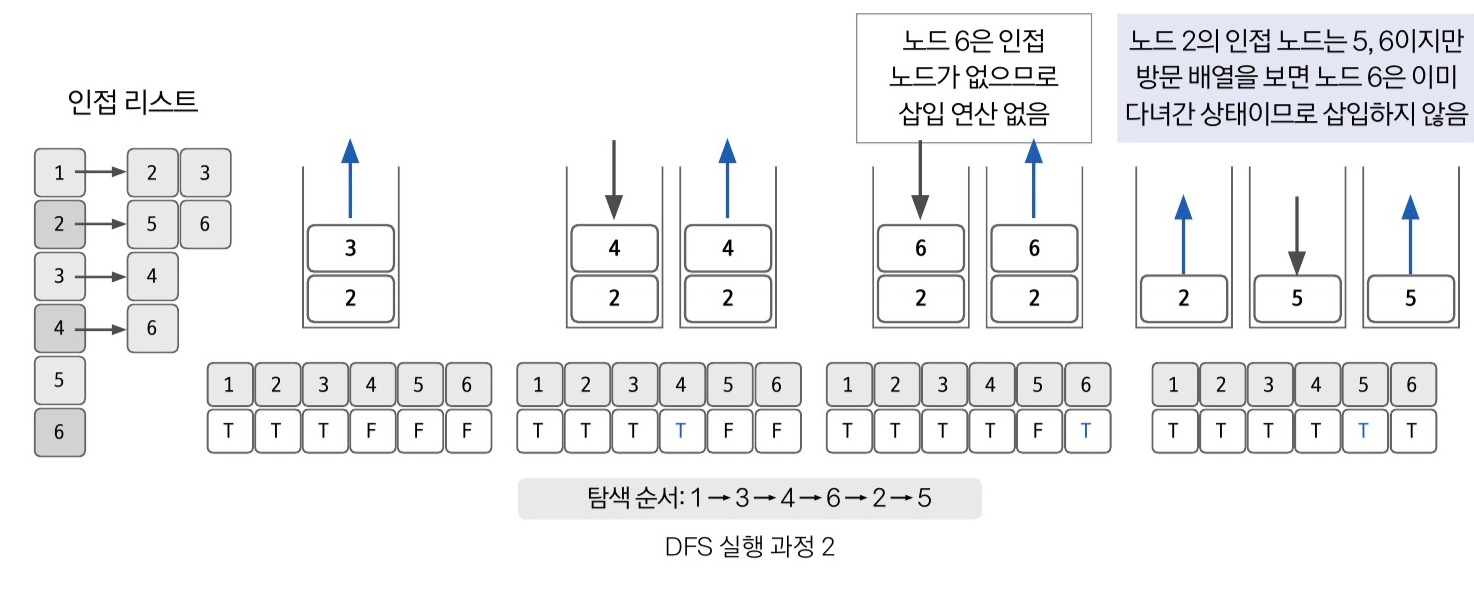
💡 결론

1. 모든 노드를 방문하고자 하는 경우에 이 방법을 선택
2. DFS가 BFS보다 좀 더 간단함
3. 모든 노드를 탐색하기 때문에 BFS에 비해 속도가 느림 → 시간 초과나면 BFS로 풀기!

👩🏻‍💻 관련문항 (백준 2023번 신기한 소수 찾기)

매커니즘

1. 1자리의 소수는 2, 3, 5, 7로 고정이므로 이를 별도의 String 배열에 넣고 for문을 돌린다. 또한, 뒷자리에 올 수 있는 수는 짝수와 5를 제외한 나머지(1, 3, 7, 9)만 가능하므로 이 또한 별도의 String 배열에 넣는다.
2. 재귀를 이용해 숫자를 만들고_dfs나 백트래킹으로 구현 가능
3. 소수인지 판별할 때는 Math.sqrt()를 활용 !! → 에라토스테네스의 체
4. 1~3 과정을 반복한 후 N자리수의 소수임이 확인되면 sb.append(prime)하기!

코드

import java.io.*;
import java.util.*;

public class BJ2023 {
	static String [] nextNum = {"1", "3", "7", "9"}; 
  // 2의배수, 5의 배수는 소수가 될 수 없음
	static StringBuilder sb= new StringBuilder();
	static int N;
	public static void main(String[] args) throws IOException{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		String [] alwaysPrime = {"2", "3", "5","7"};
		
		N = Integer.parseInt(br.readLine());
		
		for(int i = 0; i<4; i++) {
			makePrime(alwaysPrime[i], 1);
		}
		System.out.println(sb.toString());
		
	}
	static void makePrime(String s, int cnt) {
		
		if(cnt == N) {
			sb.append(s+"\n");
			return;
		}
		
		for(int i = 0; i<4; i++) {
			if(isPrime(s+nextNum[i]))
				makePrime(s+nextNum[i], cnt+1);
		}
	}
	static boolean isPrime(String s) {
		
		int tmp = Integer.parseInt(s);
		
		for(int i = 2; i<Math.sqrt(tmp); i++) {
			if(tmp % i == 0) return false;
		}
		return true;
	}
}

BFS(너비 우선 탐색)

큐를 이용해서 구현함! → 시간복잡도는 O(V+E) // V: 노드 수, E: 에지 수

• 그래프 완전 탐색 방법 중 하나로, 시작 노드에서 출발해 시작 노드를 기준으로 가까운 노드를 먼저 방문하면서 탐색하는 알고리즘
• FIFO 방식이기 때문에 큐로 구현함

핵심 이론

📌한 번 방문한 노드 재방문 불가 → 방문 체크 배열 필요
📌큐를 이용한 FIFO 방식 !

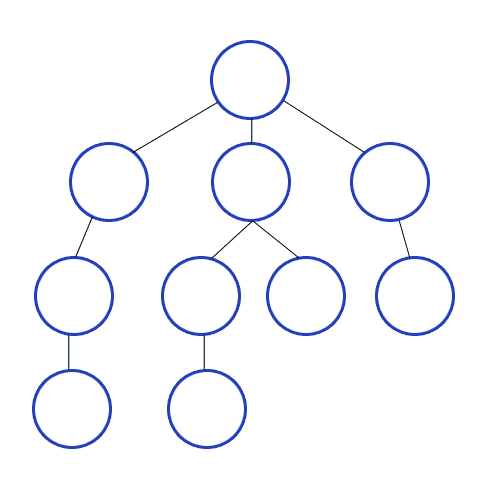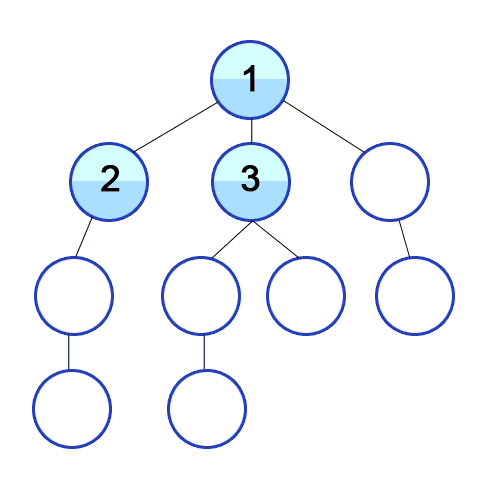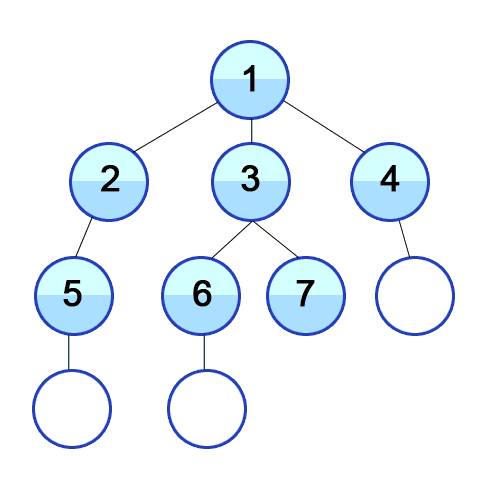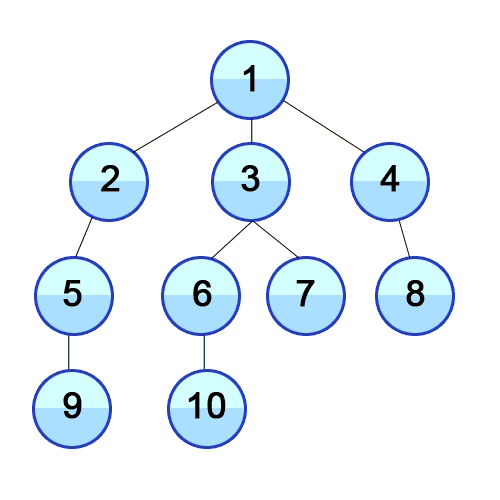
큐를 통한 구현 원리

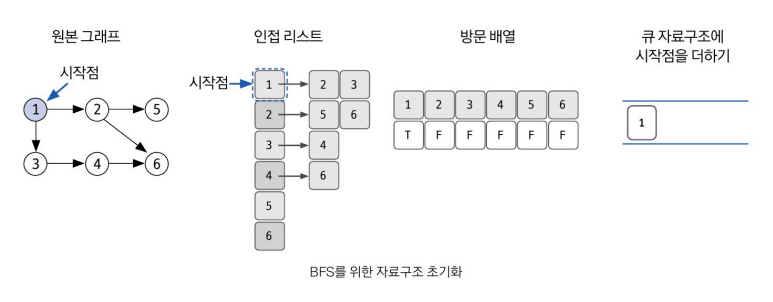
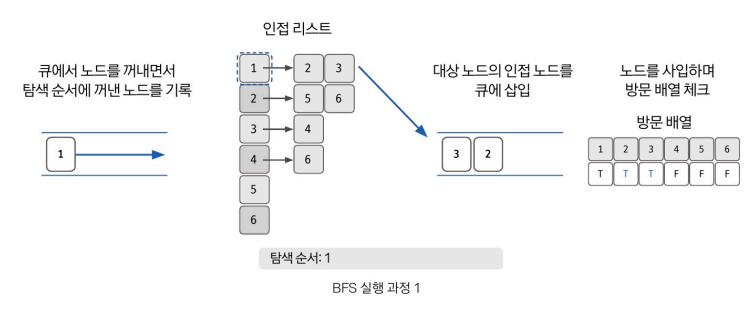
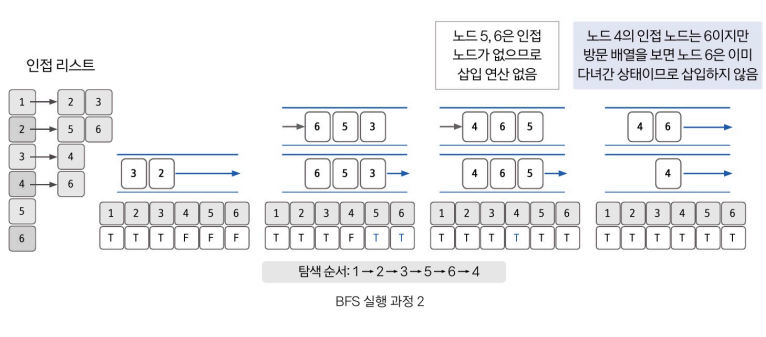
💡 결론

1. 목표 노드에 도착하는 경로가 여러 개일 때 최단 경로를 보장함
2. O(n)의 탐색 수행 시간이 소요되고 DFS 보다 수행 시간이 좋다.

👩🏻‍💻 관련문항 (백준 2468 안전영역)

package homework;

import java.io.*;
import java.util.*;
/*
5
6 8 2 6 2
3 2 3 4 6
6 7 3 3 2
7 2 5 3 6
8 9 5 2 7
 */
public class Main_bj_2468 {
	static int N;
	static int[][] map;
	static boolean[][] checked;
	static int[] dx = {1, 0, -1, 0};
	static int[] dy = {0,- 1, 0, 1};
	public static void main(String[] args) throws IOException{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		StringBuilder sb= new StringBuilder();
		
		N= Integer.parseInt(br.readLine());
		map = new int[N][N];
		
		int maxH=0;
		for(int i=0; i<N; i++) {
			st = new StringTokenizer(br.readLine());
			for(int j=0; j<N; j++) {
				map[i][j] = Integer.parseInt(st.nextToken());
				if(map[i][j] > maxH) {
					maxH =map[i][j];
				}
			}
		}
		
		int max =0;
		
		for(int h=0; h<maxH; h++) {
			checked = new boolean[N][N];
			int cnt=0;
			for(int i=0; i<N; i++) {
				for(int j=0; j<N; j++) {
					if(!checked[i][j] && map[i][j] > h){
						//cnt+=dfs(i,j,h); 
						cnt+=bfs(i,j,h); 
					}
				}
			}
			max = Math.max(max, cnt);
		}

		System.out.println(max);
	}
	// DFS탐색
	static int dfs(int x, int y, int h) {
		checked[x][y] = true;
		for(int i=0; i<4; i++) {
			int nx = x +dx[i];
			int ny = y +dy[i];
			if(nx >=0 && nx<N && ny>=0 && ny<N && map[nx][ny] > h && !checked[nx][ny]) {
				dfs(nx, ny, h);
			}
		}
		return 1;
	}
	// BFS탐색
	static int bfs(int x, int y, int h) {
		Queue<int[]> q = new ArrayDeque<int[]>();
		checked[x][y] = true;
		q.offer(new int[] {x, y});
		while(!q.isEmpty()) {
			int [] pos =q.poll();
			x = pos[0];
			y = pos[1];
			for(int d =0; d<4; d++) {
				int nx = x+dx[d];
				int ny = y+dy[d];			
				if(nx >=0 && nx<N && ny>=0 && ny<N && map[nx][ny] > h && !checked[nx][ny]) {
					checked[nx][ny] = true; // 중복될 수 있으니까 여기서 check!
					q.offer(new int[] {nx, ny});
				}
			}	
		}
		return 1;
	}
}

💭 DFS? BFS?

• 그래프의 모든 정점을 방문하는 것이 주요한 문제
  • 단순히 모든 정점을 방문하는 것이 중요한 문제의 경우 DFS, BFS 두 가지 방법 중 어느 것을 사용해도 상관없다.
• 경로의 특징을 저장해둬야 하는 문제 → 이동한 정점의 값을 가지고 계속 연산을 하는 경우(재귀적으로 호출되는경우)
  • 예를 들면 각 정점에 숫자가 적혀있고 a부터 b까지 가는 경로를 구하는데 경로에 같은 숫자가 있으면 안 된다는 문제 등, 각각의 경로마다 특징을 저장해둬야 할 때는 DFS를 사용합니다. (BFS는 경로의 특징을 가지지 못합니다)
• 최단거리 구해야 하는 문제
  • 미로 찾기 등 최단거리를 구해야 할 경우, BFS가 유리함.
  • 깊이 우선 탐색으로 경로를 검색할 경우 처음으로 발견되는 해답이 최단거리가 아닐 수 있지만,너비 우선 탐색으로 현재 노드에서 가까운 곳부터 찾기 때문에 경로 탐색 시 먼저 찾아지는 해답이 곧 최단거리 !