노드 임베딩 (정점 표현 학습)

본 포스팅은 네이버커넥트재단과 신기정 교수님(KAIST AI대학원) 자료를 참고하여 작성하였습니다

0. 정점(노드) 표현 학습

정점 표현 학습 : 그래프의 정점들을 벡터의 형태로 표현하는 것 (정점 임베딩, 노드 임베딩)

• 그래프 공간 => 벡터 공간(임베딩 공간) 으로 바꾸는 것
• 벡터로 바꾸는 이유 => 그래프에서도 기계학습 도구들을 적용하기 위함 (로지스틱 회귀분석, 다층 퍼셉트론, 군집 분석 알고리즘 등)

• 그래프간의 정점 유사도를 벡터 공간에서도 유사도가 보존되는 것을 목표로 해야함
• 벡터 공간에서의 유사도 정의방법 : 내적
  -> 그렇다면, a) '그래프 공간에서의 유사도 정의방법'과 b) '유사도를 보존하도록 임베딩 학습하는 방법'은??
  

1. 인접성 기반 접근법

• 두 정점을 연결하는 간선이 있을때(= 인접할때) 유사하다고 간주
  • 인접한경우를 1, 그렇지 않은경우를 0 으로 취급
• 한계 : 정점 사이의 거리관계, 그래프의 군집 개념을 무시하게 됨

2. 임의보행 기반 접근법

임의보행 기반 접근법에서는 한 정점에서 시작하여 임의보행을 할 때 다른 정점에 도달할 확률을 유사도로(a) 간주

• "임의보행" : 현재 정점의 이웃 중 하나를 균일한 확률로(DeepWalk 방식) 선택하는 과정을 반복하는 것을 의미
  -> 지역적 정보와 그래프 전역 정보를 모두 고려야한다는 장점이 있음

다음 그림은 정의한 유사도의 개념을 바탕으로 그래프에서의 유사도를 보존하도록 벡터로의 임베딩을 학습하는 방법이다(b)

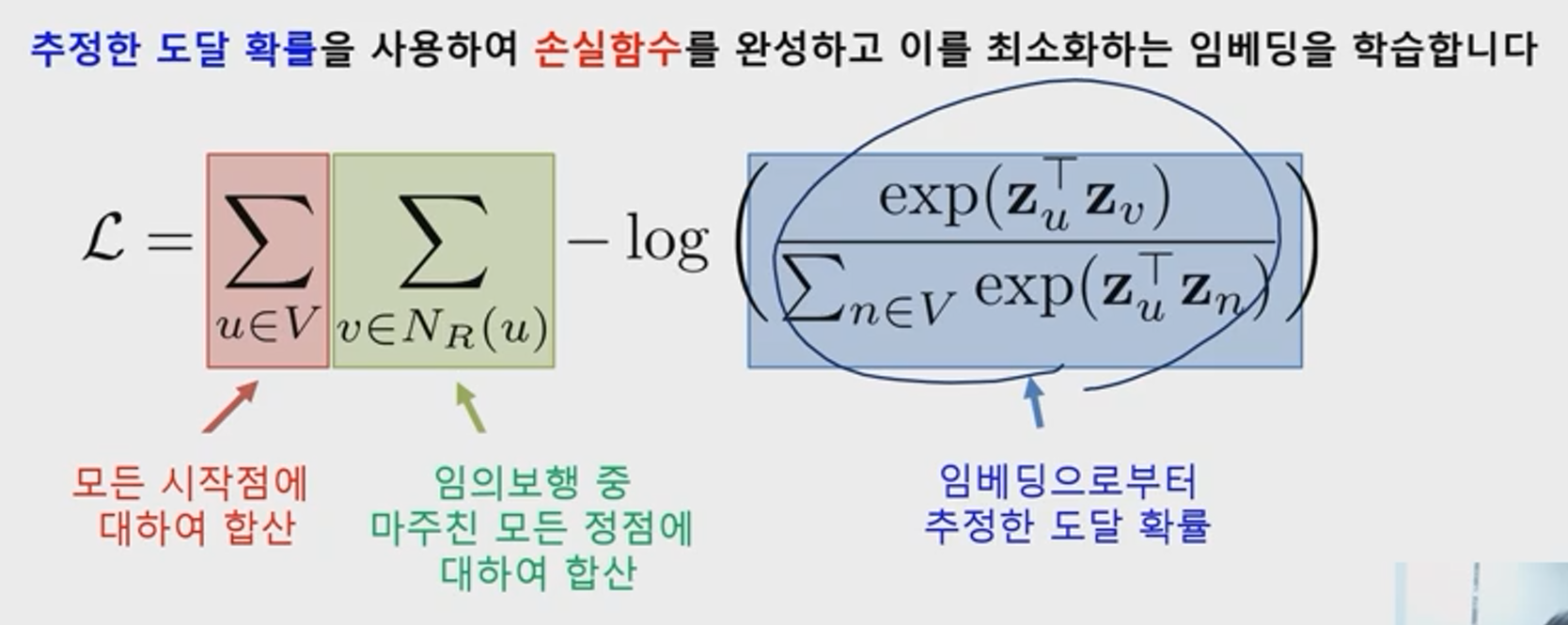
• V : 전체 노드 집합 의미
• P(v|Zu)는 '특정 노드u에서 시작한 임의보행이 v에 도달활 확률'을 임베딩으로 부터 추정한 결과
• 임베딩 공간에서의 유사도 방법인 내적값을 exp 처리하고 이를 정규한 값임
  • 이 값이 높을수록 더 낮을 손실함수가 되는셈임

임의보행의 방법에 따라 DeepWalk와 Node2Vec으로 구분됨

3. Node2Vec

• 위와 같이 현재 정점만의 이웃 중 하나를 균일한 확률로 이동하는 과정이 DeepWalk라면, Node2Vec은 '2차 츼우친 임의보행'을 사용
• 현재 정점, 직전 정점 을 모두 고려하여 다음 정점을 선택
• 직전 정점의 거리를 기준으로 경우를 구분 & 차등적인 확률 부여

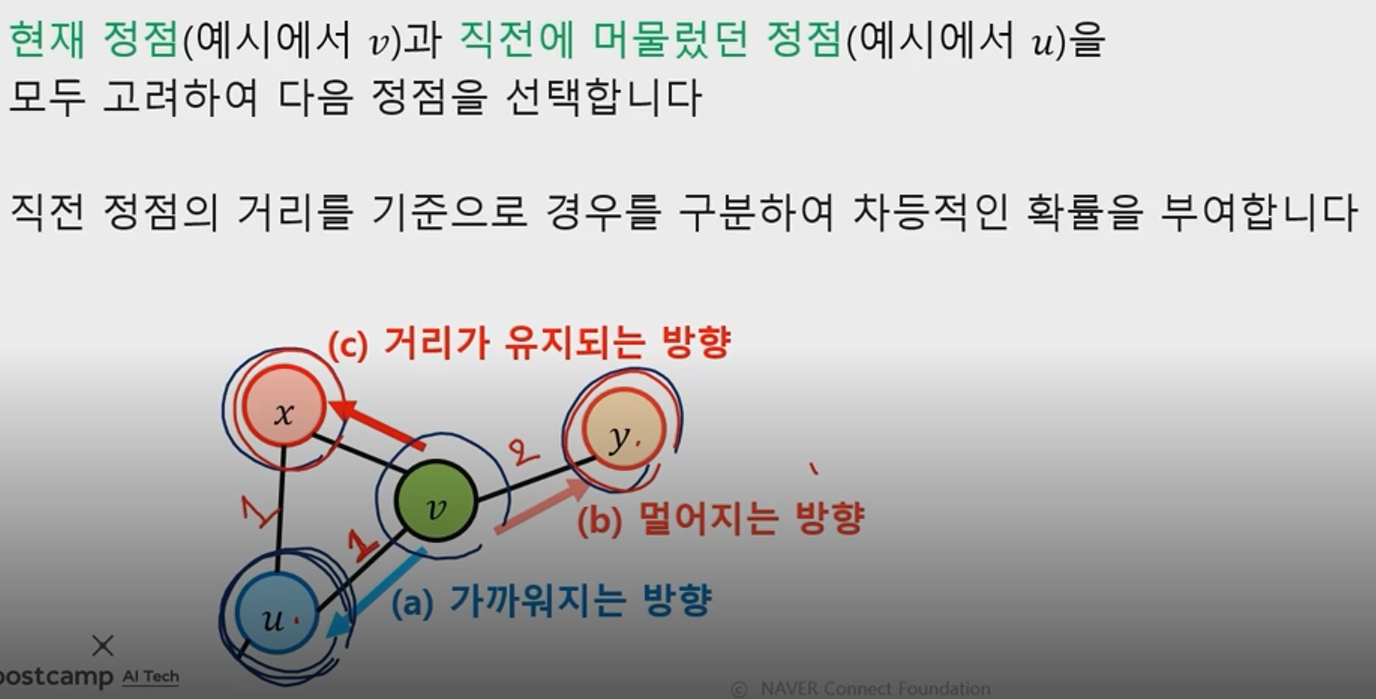
• 멀어지는 방향으로 높은 확률을 부여하는 경우 : 노드의 역할(다리 역할, 변두리 노드)이 같은 경우 임베딩이 유사하게 됨
• 가까워지는 방향으로 높은 확률을 부여하는 경우 : 같은 군집에 속한 경우 임베딩이 유사하게 됨

4. 변환식 정점 표현 학습과 귀납식 정점 표현 학습

지금까지의 위와 같은 노드 임베딩 방법들을 변환식 방법이라고 한다
- 변환식 방법 : 학습의 결과로 노드의 임베딩 자체를 얻는다
- 귀납식 방법 : 인코더(노드를 임베딩으로 변화시키는 함수)를 얻는다

변환식 임베딩 방법은 다음과 같은 한계를 갖는다

• 학습이 진행된 이후 추가된 노드에 대해서는 임베딩 공간을 얻을 수 없다
• 모든 노드에 대한 임베딩을 미리 계산하여 저장해두어야 한다
• 노드가 속성정보(부가정보)를 가진 경우에는 이를 활용할 수 없다

=> 위와 같은 단점을 극복한 것이 귀납식 임베딩으로, 대표적인 사례가 그래프 신경망 GNN(Graph Neural Network)이다