P vs NP문제?!?

P vs NP 문제

• 학문적으로 꽤 재미있는 논의가 있었던 부분
• 아직까지 풀리지않은 미해결 수학문제 7개중 하나
• 풀리면 21세기 사회에 가장 크게 공헌할 수 있다.(혹은 개인정보가 다 털리거나..)
• 2000년부터 $1M 상금이 걸려있다는데.. 20년동안 풀리지않은 문제면 못푸는 문제라고 봐야하지않나..

P분류(P class)

• 판정문제들을 분류하는 방법중 하나. 판정문제는 입력값에 대해 Yes/No 답을 내릴 수 있는 문제.
• 결정론적 튜링기계에서 다항식 시간안에 풀 수 있는 모든 문제를 포함.

결정론적 튜링 기계

• 튜링 기계: 무언가를 계산하는 기계를 대표하는 가상의 장치(일반적인 컴퓨터 알고리듬을 수행할 수 있음. 우리가 사용하는 언어는 대부분 튜링 컴플리트 언어! 블락체인쪽에서 사용하는 언어들중에서는 이를 만족하지 않는 언어가 있기도 함.)
• 결정론적 튜링기계란? 다음 단계가 분명하다. 어떤 명령이 분명하다.의 뜻이다.
• 지금 우리가 사용하는 컴퓨터가 바로 결정론적 튜링기계이다.

NP 분류(NP class)

• NP: 비결정적 다항식 시간(Nondeterministic Polynomial Time)
  • Not P가 아님!!!
• 비결정론적 튜링기계에서 다항식 시간안에 풀 수 있는 모든 문제를 포함.

비결정론적 튜링기계

• 어떤 명령어 실행 뒤, 다음 실행할 명령어가 확정되지 않음.
• 여러개의 다음 명령어를 병렬적으로 실행하는 기계이다.
• 그나마 이해하기 쉬운 비유는 우리 컴퓨터 CPU의 코어수가 무한대라 동시에 모든 명령어를 실행가능하다고 생각해보면..(그래도 어렵...)

결정론적 튜링기계에서의 NP문제

• 일단 답이 있으면, 그 답이 맞는지 다항식 시간안에 검증할 수 있음.
• 푸는데 지수시간이 걸릴 수도 있다.
  • 그래도 다항식 시간안에 검증 가능.

랜덤 접근 기계는 결정론적 튜링 기계

• 랜덤접근기계: 레지스터를 갖춘 CPU1개
• NP문제를 일반적인 방법으로 풀기에는 좀 느림
  • 대신 무작위, 근사, 휴리스틱 알고리듬 등을 이용.

P? NP?

public static boolean hasGreater(int[] nums, int k){
	for(int i = 0; i < nums.length; i++) {
    	if(nums[i] > k) {
        	return true;
        }
    }
    
    return false;
}

Q. 위 코드는 P일까? NP일까?

• 정답은 P이자 NP!?!?!?
• P인것은 알 수 있다.(다항식 시간안에 풀 수 있다. O(N)
• 병렬적으로 다항식 시간안에 풀 수 있는 문제이기에 NP이기도 하다.
  • 한 코어에서 다항식 시간 안에 풀 수 있다면 병렬적으로도 마찬가지. 따라서 P인 문제들은 모두 NP이기도 하다!
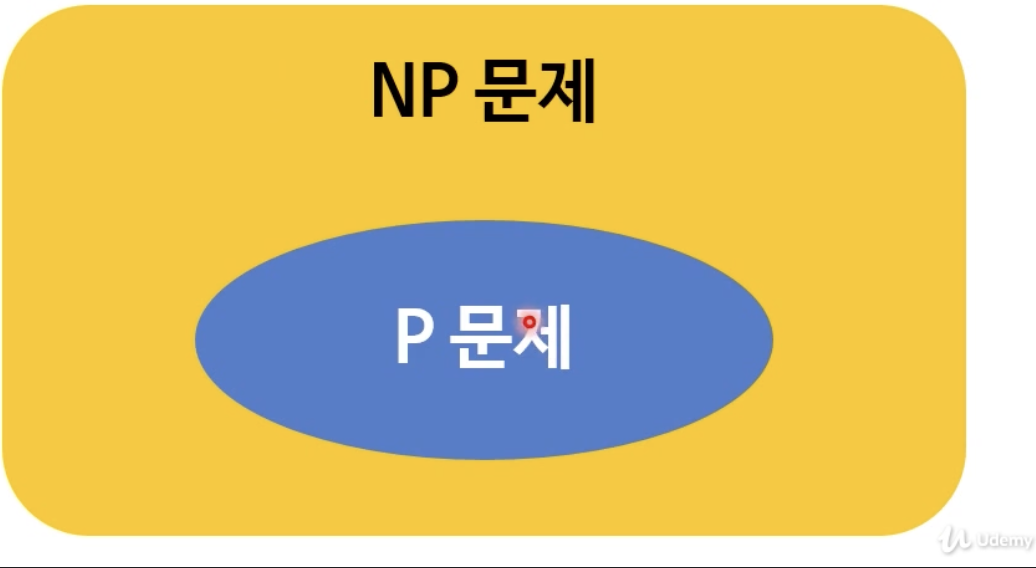
• 모든 P문제는 NP에 포함된다.
  

NP-완전(NP-complete, NPC) 문제

• NP 문제 중 일부
• 모든 NP문제들은 NP-완전문제로 환원가능
  • NP문제-NP완전문제로의 환원은 다항식 시간안에 가능.
  • 여전히 NP문제이니 다항식 시간안에 답 검증가능.
• NP완전문제는 모든 NP문제들을 환원해서 풀 수 있기 때문에 NP완전문제는 가장 어려운 NP문제라고도 할 수 있다.

NP-완전문제의 예

• 외판원 문제(판정 버전)

  1. 어떤 정해진 길이 L이 있다.
  2. 이 길이를 넘지 않는 경로가 있는지 판정

• 배낭(knapsack)문제

  1. 크기와 가격이 다른 여러 물품이 있음.
  2. 값어치가 최대가 되도록 물건 넣기
  3. 배낭 크기에는 제한이 있음.
  4. 판정버전: 최소 어떤 값어치 V만큼 넣을 수 있는가?
     • 약한 NP-완전문제: 의사다항식(다항식 보다는 좀 더 걸리는) 시간 안에 풀 수 있음.

P vs NP 문제(P == NP or P != NP 문제)

• P 또는 NP냐를 논하는 문제가 아님.
• P와 NP가 같은지 아닌지를 논하는 문제.
• NP-완전문제 중 하나라도 다항식 시간안에 풀 수 있다면?
  • 이 문제는 P가 됨.
  • 모든 NP문제를 NP-완전문제로 다항식 시간안에 환원할 수 있음.
  • 따라서 모든 NP문제가 P가 됨(P == NP) but, 이 알고리듬을 찾지 못함..!

본 내용은 Udemy의 알고리듬 및 자료구조(Java)강의를 듣고 정리한 내용입니다.