알고리듬 공부

어떤 부류의 문제를 해결하는 컴퓨터로 구현 가능한 명백한 명령어들

효율적인 알고리즘을 평가하는 기준은 시간복잡도와 공간복잡도이다.입력값의 변화에 따라 연산을 실행할 때 얼마만큼의 시간이 걸리는가이다.입력값의 변화에따라 얼마나 많은 공간(space)을 사용하는가이다

재귀란? > 재귀(recursive)란 어떤 문제를 해결가능한 작은 단위로 만드는 전략이다. 알고리듬에서의 재귀함수 위치 > 재귀함수는

모든 가능한 경우의 수를 시도하는 알고리듬문제에따라 더 효율적인 알고리듬이 없는 경우가 있기때문!

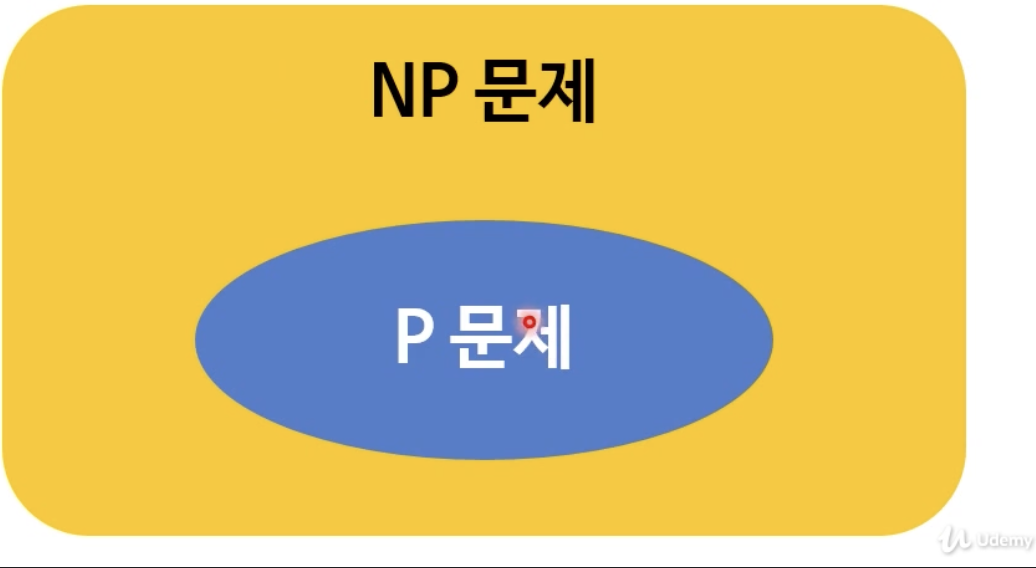
학문적으로 꽤 재미있는 논의가 있었던 부분아직까지 풀리지않은 미해결 수학문제 7개중 하나풀리면 21세기 사회에 가장 크게 공헌할 수 있다.

탐색과 검색은 컴퓨터에서 매우 흔하고 중요하다.데이터가 많아질 때 탐색속도가 현저히 줄어들 수 있다. 그럴때 사용하는것이 바로 이진탐색이다.

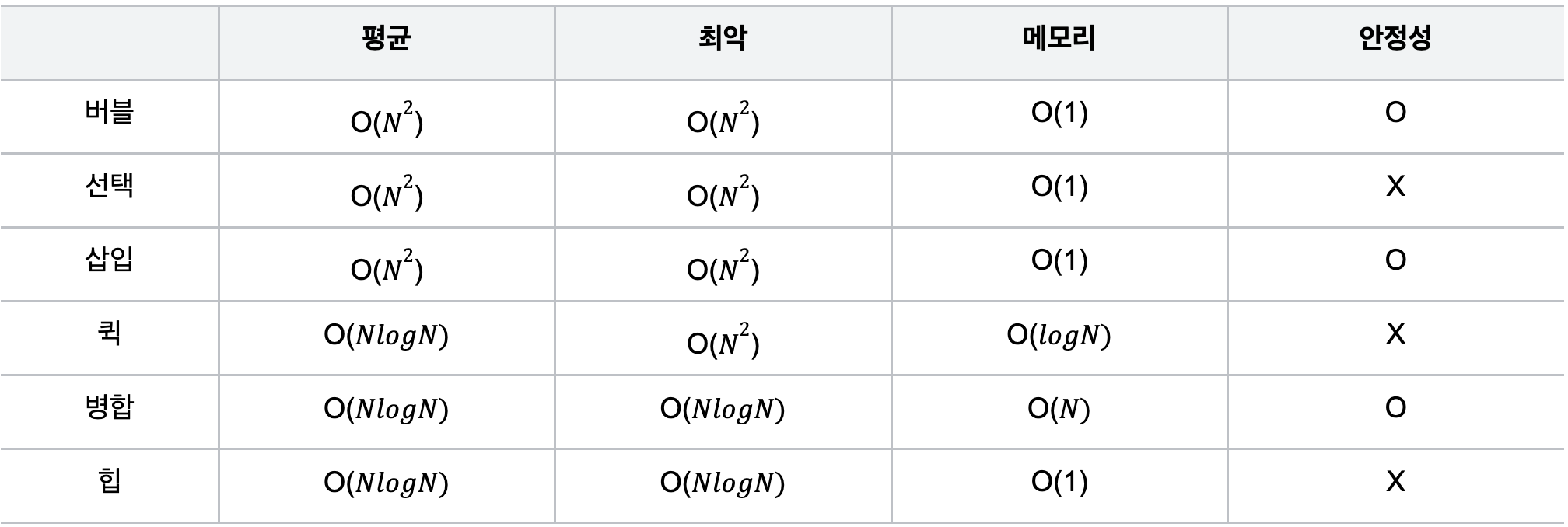
목록 안에 저장된 요소들을 특정한 순서대로 재배치하는 알고리듬사람이 읽기 편하도록 하기위해 && 더 효율적인 알고리듬 사용을 위해 사용됨.

해시함수의 정의와 속성 해시(hash)는 컴퓨터공학에서 매우 근본이 되는 알고리듬 중 하나 정의 > 임의의 크기를 가진 값을 고정 크기의 값에 대응시키는 함수 > 여전히 함수이므로 수학에서의 함수의 정의도 만족해야 함

해시값에서 원본 값을 찾는게 사실상 실행 불가능한 알고리듬 현실적으로 어마어마한 컴퓨팅 파워가 필요해 실행이 불가능에 가깝다는 의미.

평문(plaintext)을 암호문(ciphertext)으로 변환하는 것.암호문도 누군가 훔쳐볼 수 있다. but, 특별한 정보를 아는 사람만 이해할 수 있음.암호문을 다시 평문으로 변환하는 것 = 복호화(decryption)해시알고리듬은 원문 복구를 막는게 목표

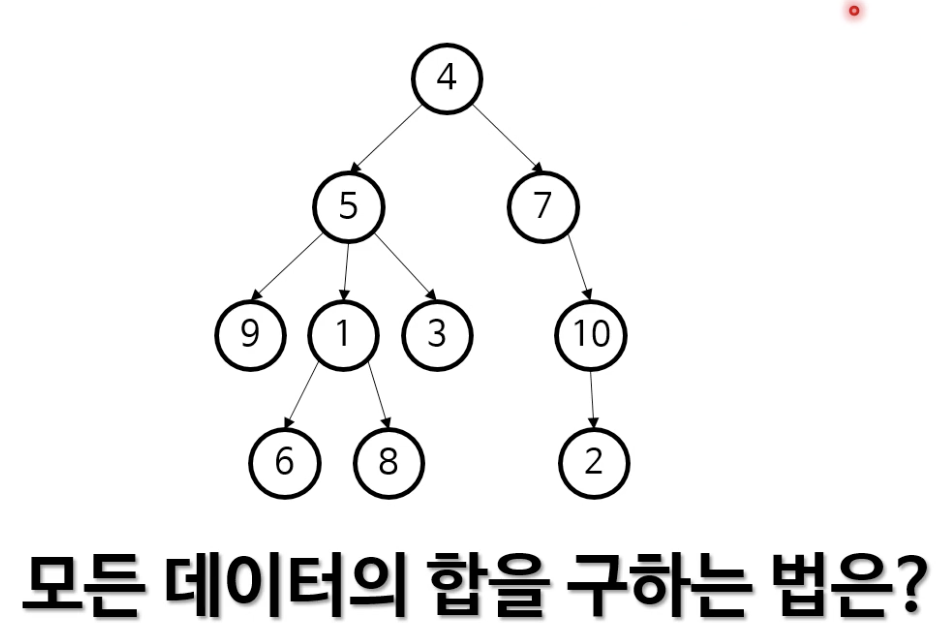
자료구조이기도하고 트리 알고리듬도 존재함.알고리듬 공부를 했는지에대해 파악할때 트리까지는 잘 물어봄트리는 실무에서 사용할 일이 많음매우 널리 사용하는 자료구조중 하나나무(tree)의 계층적 구조를 표현

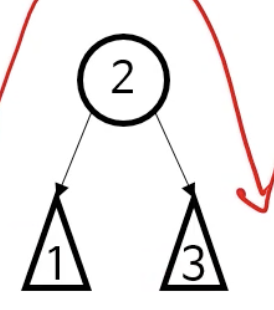
대표적인 3가지 순회법전위(pre-order) 순회중위(in-order) 순회후위(post-order) 순회중위 : 왼쪽 하위트리 -> 현재노드 -> 오른쪽 하위 트리전위 : 현재노드 -> 왼쪽 하위트리 -> 오른쪽 하위 트리후위 : 왼쪽 하위트리 -> 오른쪽 하위 트

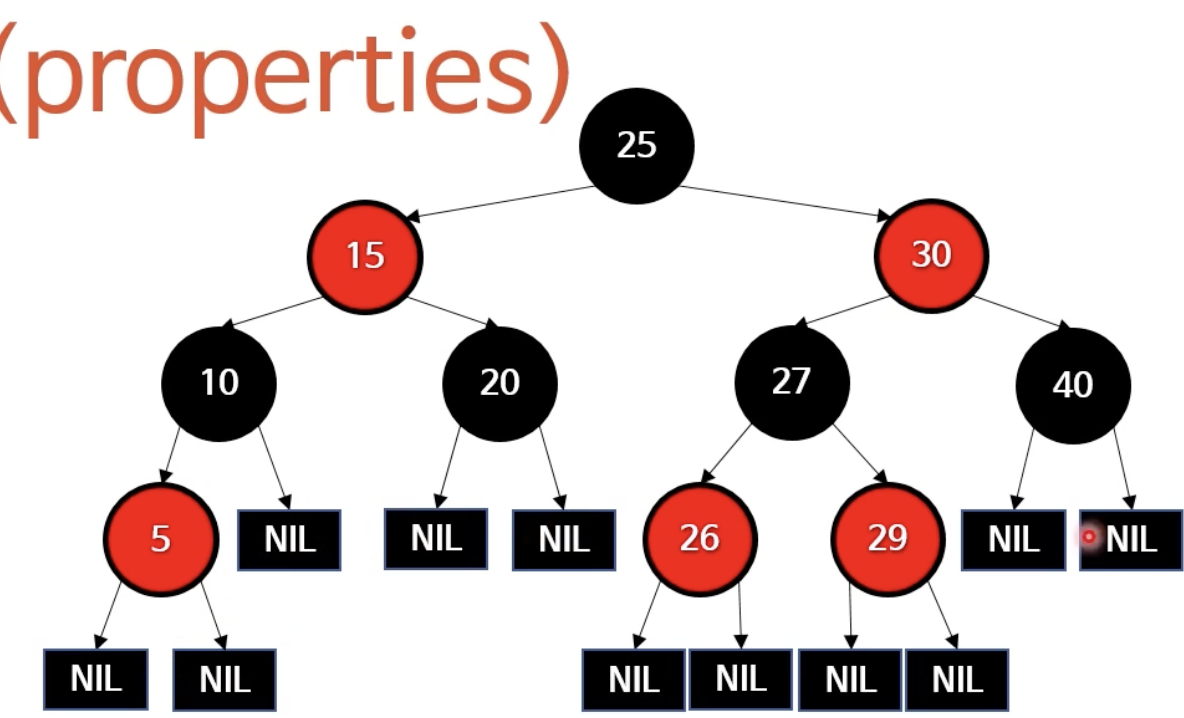
각 노드가 레드 혹은 블랙노드에 저장하는 데이터가 아님그냥 1비트짜리 추가 정보(굳이 빨강/검정이 아니어도 되지만, 일반적으로 레드/블랙을 사용한다고 함)스스로 균형을 잡는(self-balancing)트리트리 높이를 최소로 보장균형을 잡는 시점은 삽입/삭제시그외 연산은

레드-블랙트리의 특성을 유지하기위해 어떤 연산을 해야할까?탐색: 이진 탐색트리와 같음단, O(logN)을 보장함!삽입과 삭제일단 삽입 혹은 삭제실행(특성이 망가질 수 있음)그 후, 망가진 특성을 고치기위해 트리의 구조를 재배치(회전)혹은 노드 색을 바꿈완벽하진 않으나

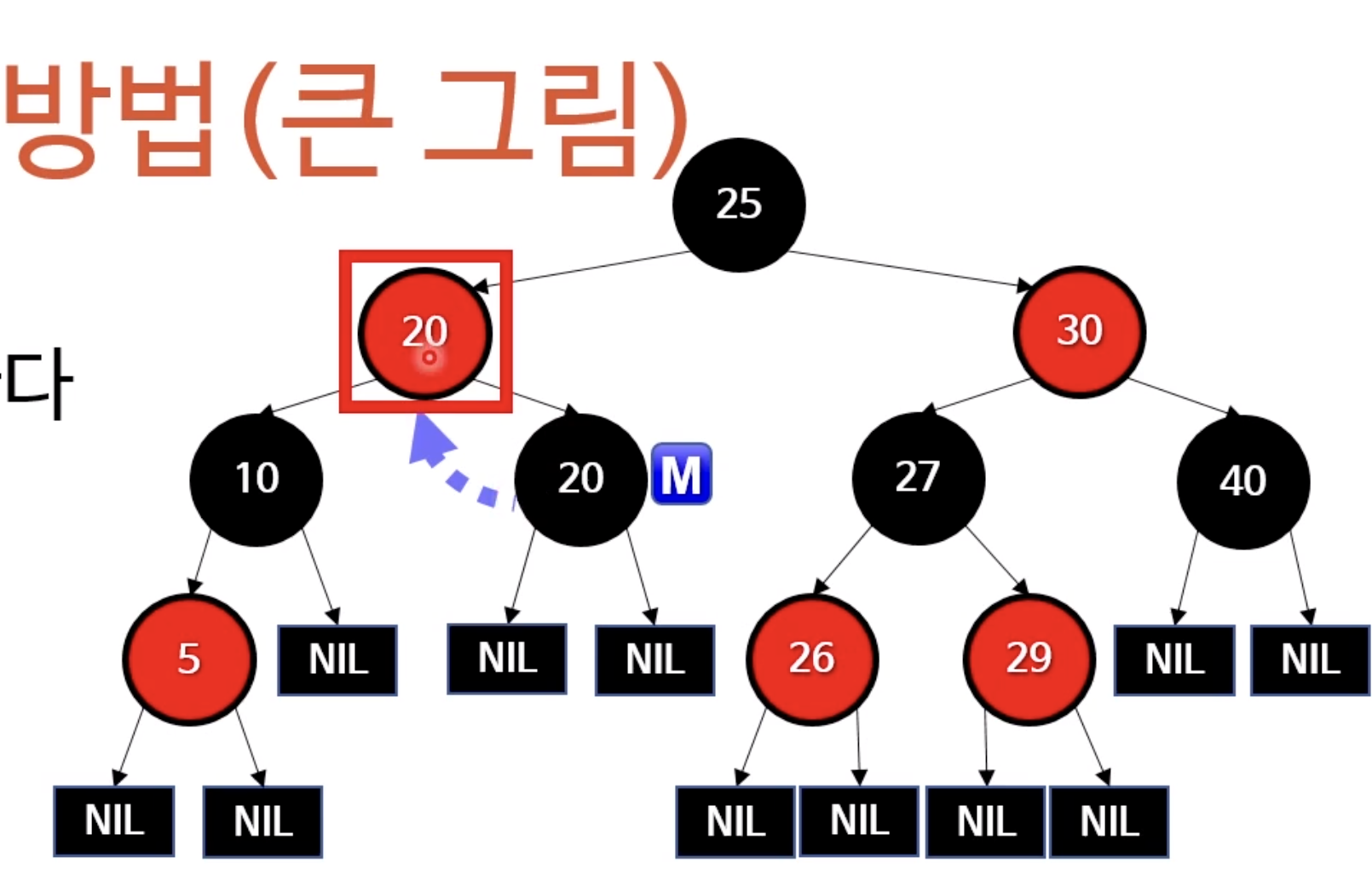
설명이 어려운 내용.비유를 통해서도 암기를 돕기 어려움.케이스가 너무 많아서 감을 잡는것이 목표지우려는 값을 가진 노드를 찾음교환할 NIL이 아닌 노드 M을 찾음값을 복사해옴(색은 복사안함)M을 지움M은 언제나 오른쪽(혹은 왼쪽) 하위트리의 최솟값M의 왼쪽에 다른 값이