[자료구조] Stack & Queue

바닐라JS로 테트리스 만들기 하던 중, call stack error를 일으키는 재귀함수에 대해 알게 됐고, 방지하기 위해 setTimeout() 메서드 안에 따로 배치하는 것을 확인했다.
물론 오늘의 글은 call stack error가 아닌 call stack error의 stack을 알기 위함이다. 틈틈이 자료구조 공부도 하고, 개념을 익히기 위해 실제 코드 사용 중, 확인하게 되는 문제나 궁금한 점들을 기록하기로 한다.

---

자료구조에서 그 의미를 정의할 때, 스택과 큐를 함께 비교하곤 한다. 우선 그림을 통해 스택과 큐의 차이점에 대해 알아보자.

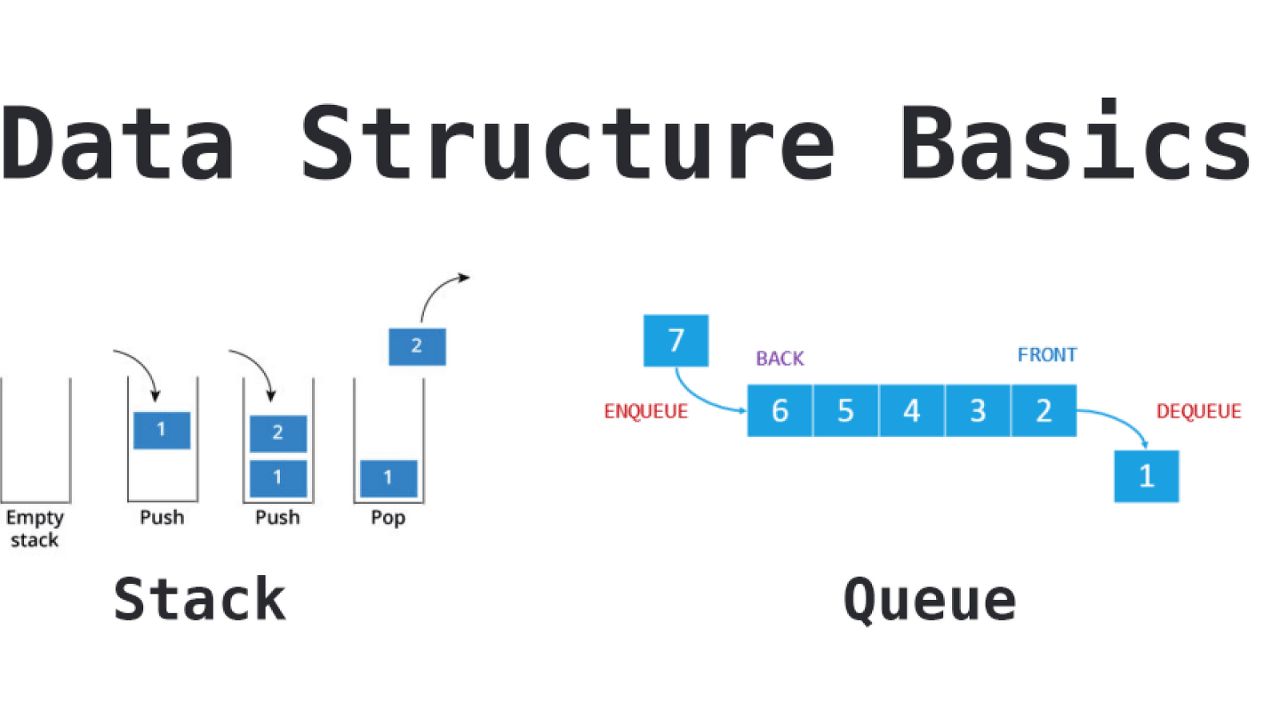
1. 스택(Stack)

정의

• 선형리스트 구조의 특별한 형태 : 데이터 삽입과 삭제가 top에서만 일어나는 구조
• push down 리스트 또는 LIFO(Last In First Out) 리스트
  - 데이터 삽입과 삭제가 한 곳에서 일어나므로, 가장 늦게 삽입된 데이터가 가장 먼저 삭제됨.

사용분야

• 서브 루틴의 복귀 주소(return address)를 저장할 경우
• 수식 계산

---

1-1. 스택 표현과 연산

스택 표현

• 1차원 배열 표현 : 스택이 포함할 수 있는 최대 크기를 알 수 있을 때
• 연결 리스트로 표현 : 스택의 최대 크기를 알 수 없을 때

연산

• push(x) : 스택에 데이터 x를 삽입하는 연산, top의 값을 1씩 증가
• pop() : 스택의 데이터를 삭제하는 연산, top의 값을 1씩 감소

---

1-2. 스택의 배열 구현

스택 선언

• item 배열 : 스택의 항목
• top : 현 스택의 top 위치

#define MAXSTACK 100
struck stack {
	int item[MAXSTACK];
};

struct stack *s;

항목 유뮤 조사

• 공백인 스택 : top == -1;

if (s -> top == -1)
print f("stack is empty");
else
print f("stack is not empty")

항목 삭제

int pop (struck stack *s) {
	int popp;
    
    if (s -> top == =1){
    	print f("stack underflow");
        exit(1)'
    }
    popp = s -> item[s -> top--];
    return(popp);
}

항목 삽입

void push(struck stack *s, int x){
	if (s -> top == MAXSTACK - 1){
    	print f("stack overflow");
        exit(1);
    }
s -> item[++s -> top] = x;
}

---

1-3. 스택 오버플로우 처리

하나의 기억장소에 2개 스택을 보관 운영하는 방법

• top : 입출력이 발생되는 스택의 끝
• bottom : 스택의 시작 위치

하나의 기억장소에 n개의 스택을 보관 운영하는 방법

• topi = bottomi 이면 i 번 째 스택의 empty
• topi = bottomi+1 이면 i 번 째 스택의 포화 상태
• topi > bottomi+1 이면 i 번 째 스택의 오버플로우
  • 기억 장소의 빈 공간을 찾아 기억 공간을 재압축(repacking)

---

1-4. 수식 계산

연산자 우선순위

• 연산에서 괄호가 없을 경우, 혹은 괄호 내 우선순위

연산자	우선순위
단항연산자 -, !	6
*, /, %	5
+, -	4
<, <=, >, >=	3
&&	2
||	1

---

---

2. 큐(Queue)

정의

• 한쪽 끝에서 항목들이 삭제되고, 다른 한쪽 끝에서 항목들이 삽입되는 선형 리스트(파이프 형태라 생각하면 됨)
• FIFO(First-In Fisrt-Out) : 가장 먼저 삽입된 항목이 가장 먼저 삭제

응용

• 작업 스케줄링, 대기 행렬 이론(queueing theory)

---

2-1 큐의 배열 표현과 연산

큐의 표현

• 1차원 배열 : Queue[T]
  Queue = [Q0, Q1, Q2, ... QT-1]
  front(Q) = Q0
  rear(Q) = T-1
  - front : 실제 큐의 front보다 하나 앞을 가리킴
  - rear : 실제 큐의 rear
  - 큐가 빈 상태 : front = rear
  - 큐의 초기 조건 : front = rear = -1
  

---

2-2 큐의 배열 구현

큐 선언

struck queuestruck {
	int queue[100];
    int f, r;
};

struck queuestruck *q;

항목 삽입

void AddQueue(struck queuestruck *q, int item) {
	if(q -> r = = MAXQUEUE - 1) q_full();
    /* 단, MAXQUEUE는 해당 큐의 크기 */
    else {
    	q -> queue[++q -> r] = item;
    }	
}

항목 삭제

int DeleteQueue(struck queuestruck *q){
	if (q -> f == q -> r) q_empty();
    else {
    	return (q -> queue[++q -> f]);
    }
    return (0);
}

---

2-3. 큐의 단점과 해결책

큐의 단점

• rear가 배열의 마지막 원소를 가리키는 경우 (rear == MAXQUEUE - 1)가 반드시 MAXQUEUE개의 항목이 차 있는 것을 의미하지 않음.
• front == -1, rear == MAXQUEUE - 1이면 오버플로우
• front가 -1보다 크면 데이터 항목이 삭제된 것이므로 큐에 빈 공간이 남아 있음
• 계속 항목을 삭제하면 rear pointer와 front pointer가 만나게 되고 공백 큐가 되는데도 오버플로우 현상 발생

해결책

• 큐 전체를 왼쪽으로 옮기고 front를 -1로 하고 rear 값을 조정
• 원형 큐
  - 큐 배열을 선형으로 표현하지 않고 원형으로 표현하는 방법
  

---

2-4. 원형 큐(circlar Queue)

원형 큐의 정의

• 큐 배열(arrangement)을 원형으로 표현
• 큐 구성 배열의 처음과 끝을 이어놓은 형태

항목 삭제

int deleteQ(struck queuestruck *q){
	int item;
    if(q -> f == q -> r){
    	q_empty();
    } else {
    	q -> f = (q -> f + 1) % MAXQUEUE;
        item = q -> queue[++q -> f];
        return (item);
    }
}

---

---

3. 데크(Deque: Double Ended Queue)

정의

• 삽입과 삭제가 양쪽 끝에서 모두 허용될 수 있는 선형 리스트
• 스택과 큐를 선형리스트 구조에 복합시킨 형태
• 두 개의 스택의 bottom 부분이 서로 연결된 형태

---

3-1. 데크의 표현 및 연산

스택을 이용하는 경우

• 두 개의 스택을 연결
• 스택들이 뚜렷한 경계가 있거나, 스택의 마지막 원소의 위치를 저장할 수 있다면, 스택들이 같은 기억 장소 공유 가능
• 기억 장소 오버플로우 발생
• 양쪽 끝에서 삽입/삭제 가능하기 때문에 두 개의 포인터(left, right 또는 top, bottom) 필요

연결 리스트를 이용하는 경우

• 한 데이터 항목을 첨가해야 할 때 사용 가능한 기억 공간을 확보해 주는 함수 이용
• 원소 삭제될 때에는 기억 장소 관리 함수를 이용하여 반환

3-2. Deque 종류

입력 제한 데크

• 입력이 한쪽 끝에서만 일어나도록 제한(스크롤)

춣력 제한 데크

• 출력이 한쪽 끝에서만 일어나도록 제한(셀프)