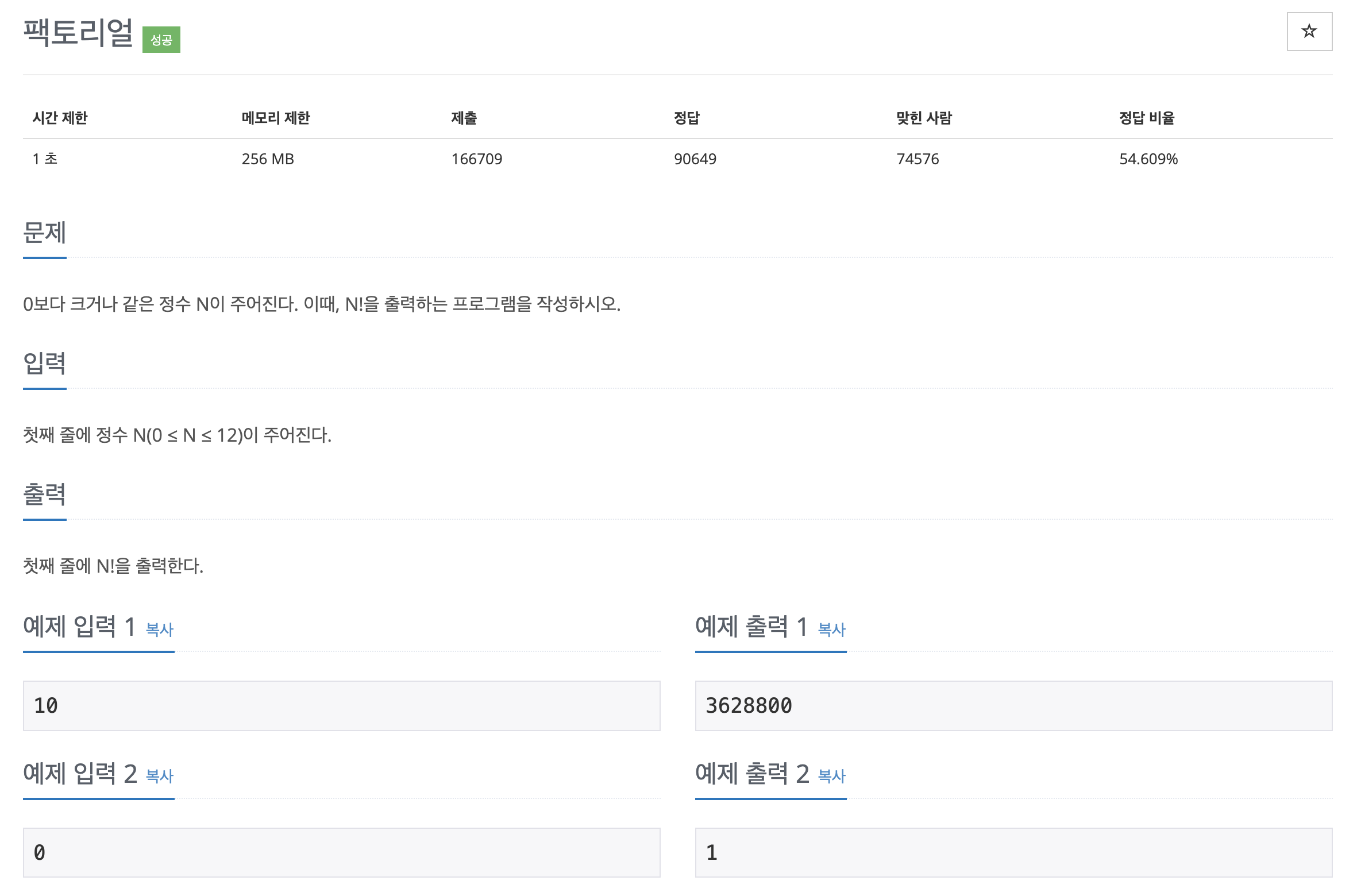
문제 10872. 팩토리얼

재귀호출 함수의 대표적 예시인 팩토리얼 구하는 함수로 풀었다.
탈출 조건이 필수로 있어야 한다. 그렇지 않으면 무한으로 호출하다가 스택 오버플로우가 발생한다.

#include <stdio.h>

int factorial(int num);

int main(void)
{
  int num;
  scanf("%d", &num);

  printf("%d\n", factorial(num));

  return 0;
}

int factorial(int num)
{
  if (num <= 1) return 1;
  return num * factorial(num - 1);
}

이전 글에서 작성했듯이 main 함수 위에 factorial 함수를 선언하고, main 함수 안에서 다른 함수를 정의할 수 없기 때문에 main 함수 아래에 factorial 함수를 정의했다.

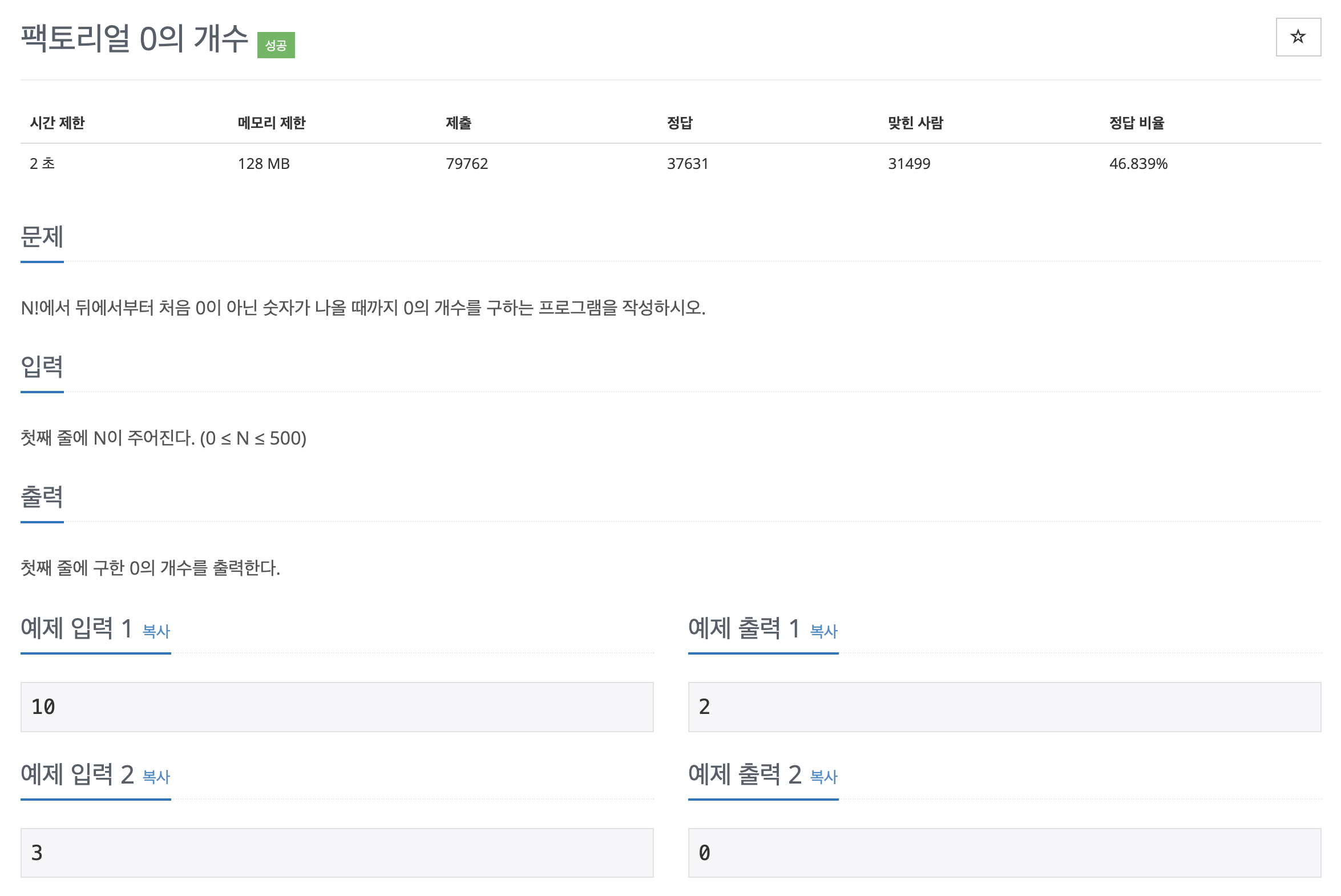
문제 1676번. 팩토리얼 0의 개수

처음에는 이 문제도 똑같이 팩토리얼을 재귀 함수로 구하고, 그 다음 0의 개수를 세는 방식으로 풀었다. 그러나...

시간 초과로 바로 컷 당하고... 다시 읽어보니 이 문제에서는 N이 최대 500이었다. 500!은 long long으로도 담을 수 없는 무지막지한 숫자이다. 팩토리얼을 직접 구해서 풀지 말라는 뜻이다.

그럼 어떻게 해야 할까?
2와 5를 곱하면 끝 자리에 0이 생긴다. 즉 N!을 소인수분해했을 때 인수 2의 개수와 인수 5의 개수 중 더 작은 수가 0의 개수가 된다. 그런데 1부터 N까지의 자연수 중에서는 2의 배수 개수가 5의 배수 개수보다 같거나 더 많을 수밖에 없기 때문에 어차피 인수 5의 개수만 세면 된다.

#include <stdio.h>

int main(void)
{
  int num, count = 0;
  scanf("%d", &num);

  for (int i = 1; i <= num; i++) // 1부터 N까지 반복
  {
    if (i % 5 == 0) {
      int divisor = i;      
      do
      {
        count++;
        divisor /= 5;
      } while (divisor % 5 == 0 && divisor / 5 >= 1);
    }
  }
  
  printf("%d\n", count);
  
  return 0;
}

1부터 N까지 반복문을 한 번 돌면서, i가 5의 배수이면 count를 센다.
그런데 25, 125 같은 경우에는 인수 5를 한 개만 갖고 있는 게 아니라 2개, 3개씩 갖고 있다. 그럴 경우 count도 2, 3씩 세어주어야 한다. i를 반복문 내부에서 변경하면 안 되므로 다른 변수(divisor)에 복사해주고, 5로 나누어떨어지는 자연수인 동안은 계속 5로 나누면서 count를 세는 것을 반복한다. 예를 들면 divisor가 125일 때 125 → 25 → 5까지 계속 count를 세고 1이 되면 do ~ while문을 탈출한다.

성공!