이진 검색,선택 정렬, 큌 정렬

이진 탐색이란?

이진 탐색이란 데이터가 정렬돼 있는 배열에서 특정한 값을 찾아내는 알고리즘이다. 배열의 중간에 있는 임의의 값을 선택하여 찾고자 하는 값 X와 비교한다. X가 중간 값보다 작으면 중간 값을 기준으로 좌측의 데이터들을 대상으로, X가 중간값보다 크면 배열의 우측을 대상으로 다시 탐색한다. 동일한 방법으로 다시 중간의 값을 임의로 선택하고 비교한다. 해당 값을 찾을 때까지 이 과정을 반복한다.

이진 탐색은 매우 빠른 속도로 데이터를 찾을 수 있지만반드시 데이터가 정렬되어있어야만 한다.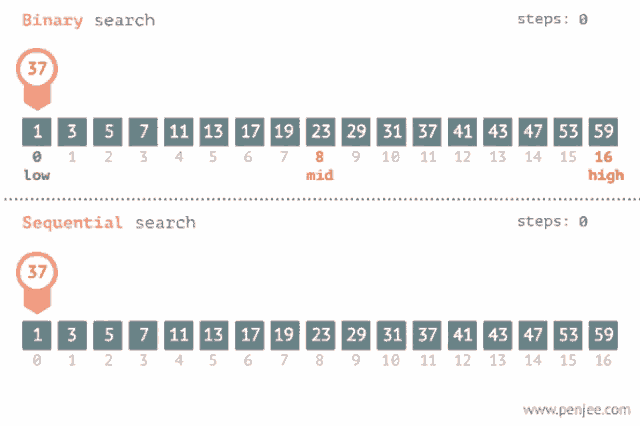

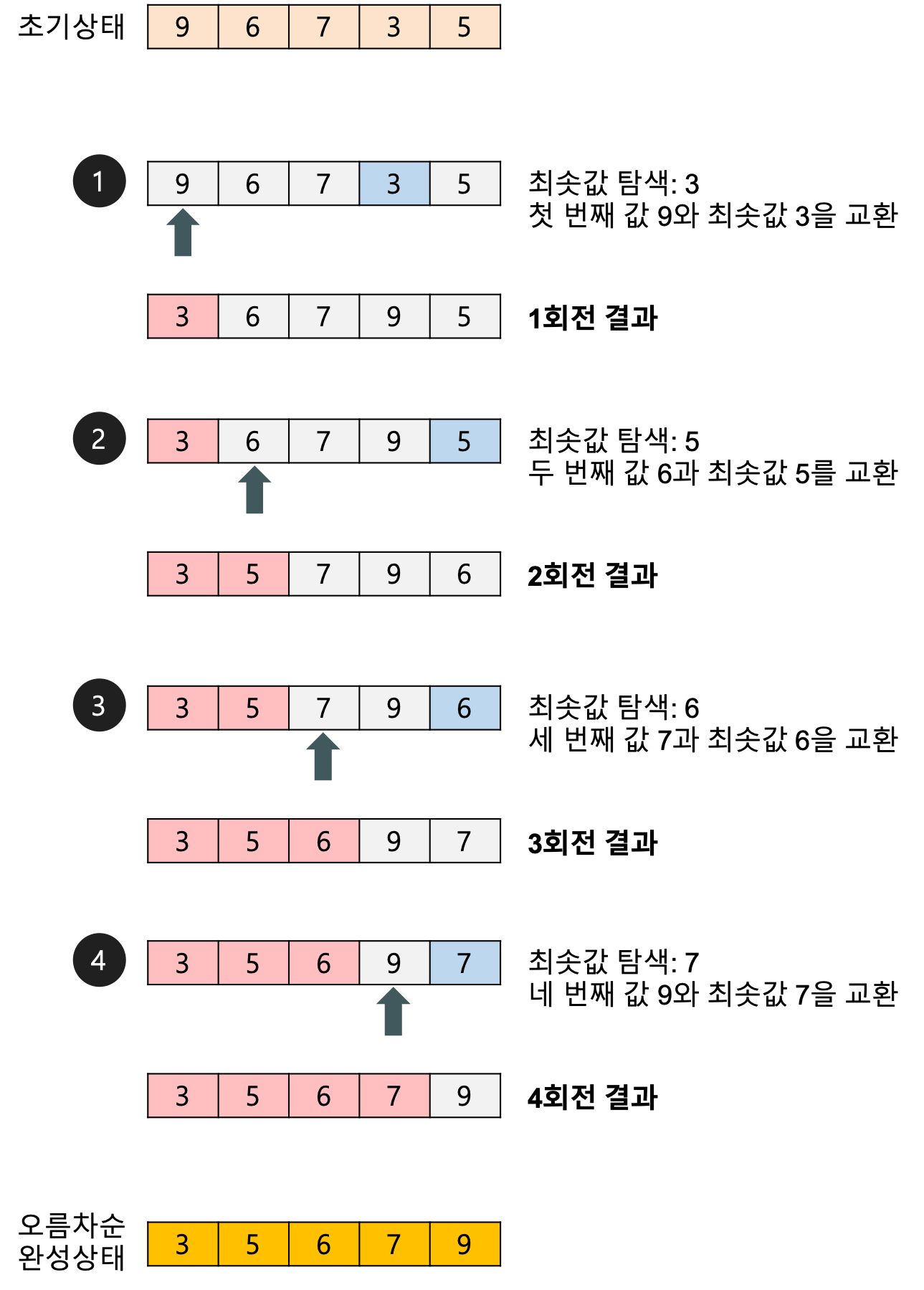
이진 검색을 활용하여 js 로 알고리즘 구현 화면

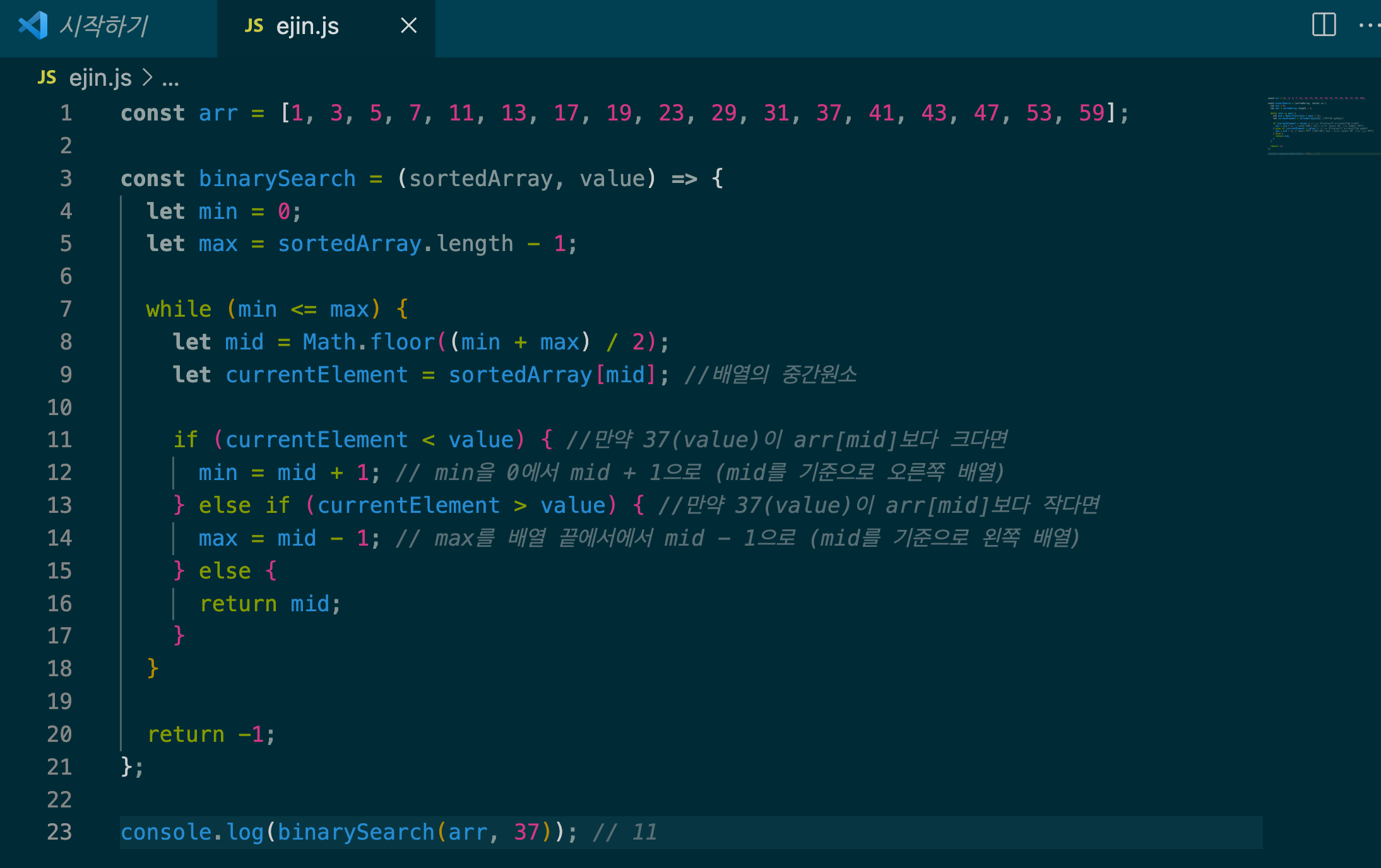
1. 배열의 가운데 원소(arr[mid])와 탐색하고자 하는 값 37을 비교한다.
2. 만약 37(value)이 arr[mid]보다 작다면 -> 이진 탐색(mid를 기준으로 배열의 좌측 절반을 순환 호출)
3. 만약 37(value)이 arr[mid]보다 크다면 -> 이진 탐색(mid를 기준으로 배열의 우측 절반을 순환 호출)

만약 배열중에 원하는 숫자가 없으면 -1을 리턴

• 분할 - mid를 기준으로 왼쪽, 오른쪽 배열으로 분할, value와 arr[mid]가 같다면 값을 반환 후 종료
• 정복 - value가 arr[mid]보다 작으면 mid를 기준으로 좌측 이진 탐색, 크면 우측 탐색
• 결합 - 탐색 결과가 직접 반환되어 결합은 필요하지않음

마지막 11번째있다는걸 보여줍니다

자바 알고리즘 이진 검색

public class BinarySearch {
	public static void main(String[] args) {
		int[] arr = { 1, 2, 3, 4, 5, 6, 7, 8, 9 };

		binarySearch(2, arr);
	}

	public static void binarySearch(int iKey, int arr[]) {
		int mid;
		int left = 0;
		int right = arr.length - 1;

		while (right >= left) {
			mid = (right + left) / 2;

			if (iKey == arr[mid]) {
				System.out.println(iKey + " is in the array with index value: " + mid);
				break;
			}

			if (iKey < arr[mid]) {
				right = mid - 1;
			} else {
				left = mid + 1;
			}

		}
	}
}
출처: https://blog.opid.kr/489 [opid's document:티스토리]

선택 정렬

제자리 정렬(in-place sorting) 알고리즘의 하나
입력 배열(정렬되지 않은 값들) 이외에 다른 추가 메모리를 요구하지 않는 정렬 방법
해당 순서에 원소를 넣을 위치는 이미 정해져 있고, 어떤 원소를 넣을지 선택하는 알고리즘
첫 번째 순서에는 첫 번째 위치에 가장 최솟값을 넣는다.
두 번째 순서에는 두 번째 위치에 남은 값 중에서의 최솟값을 넣는다.
…
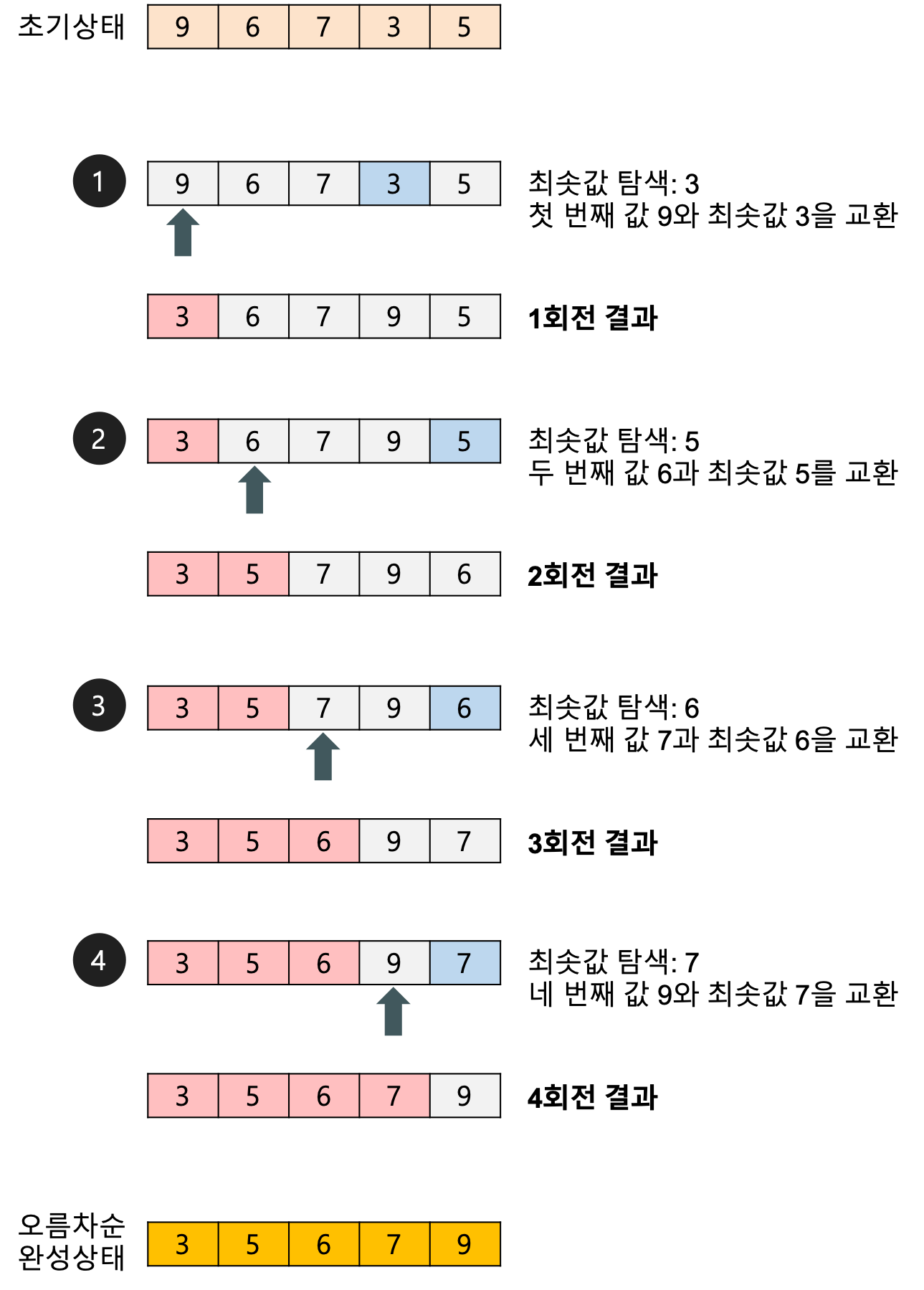
과정 설명
1.주어진 배열 중에서 최솟값을 찾는다.
2.그 값을 맨 앞에 위치한 값과 교체한다(패스(pass)).
3.맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체한다.
4.하나의 원소만 남을 때까지 위의 1~3 과정을 반복한다.

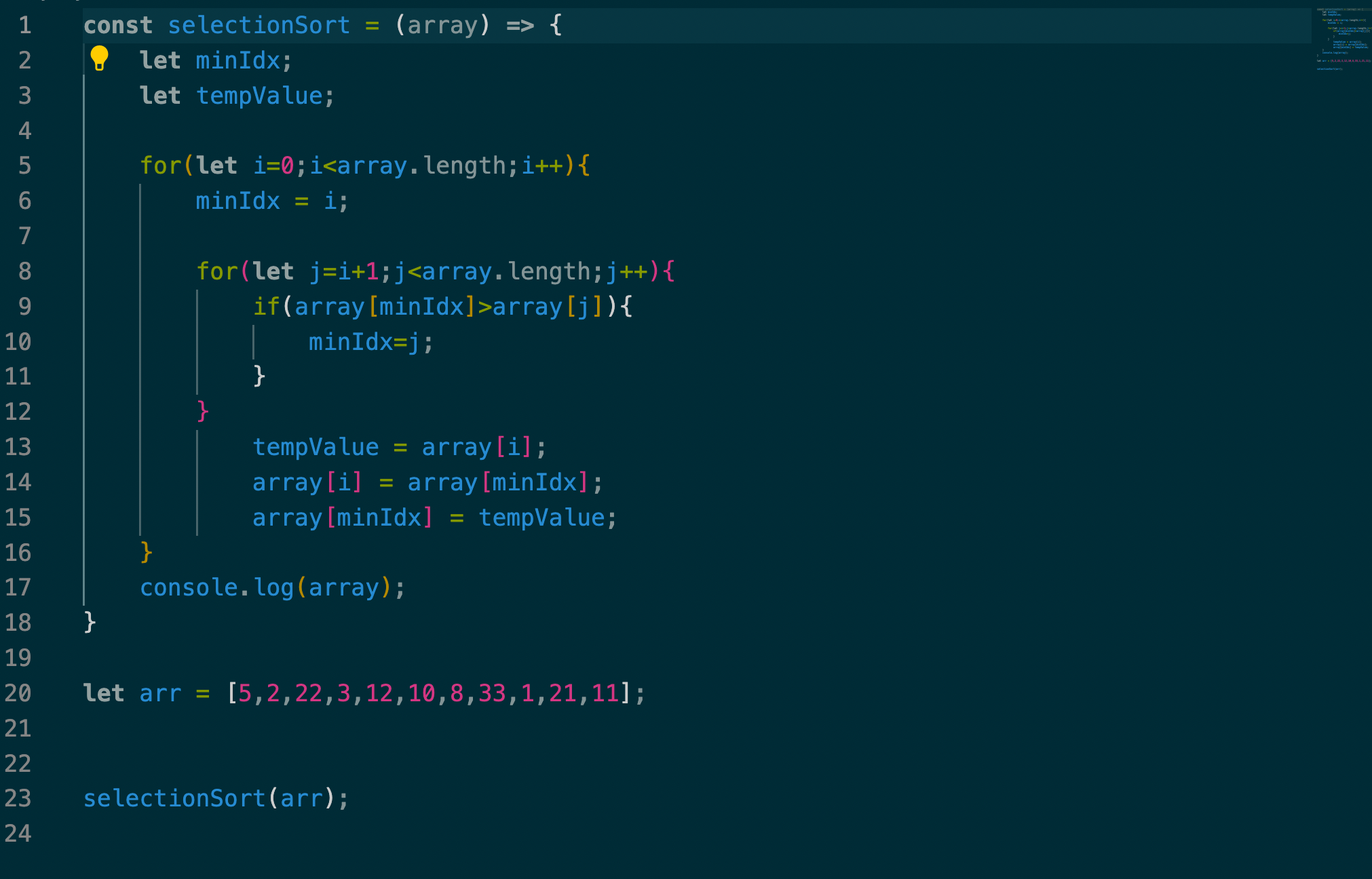
선택 정렬 알고리즘

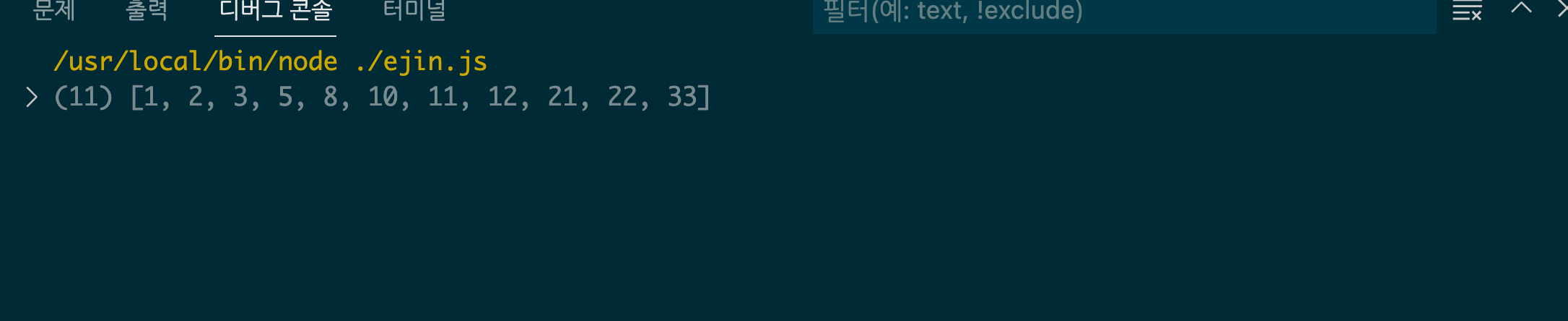
나온 결과값

하지만 스크립트는 arr.sort((a, b)⇒ a - b) sort 메소드로 쉽게 오름차순 할수 있습니다

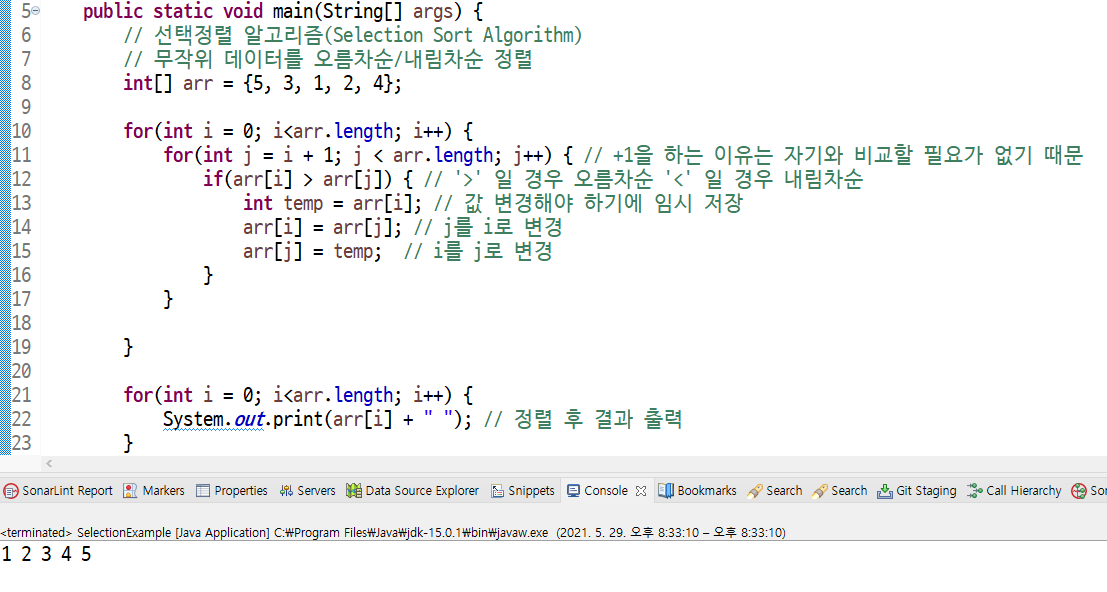
// 자바 선택 정렬

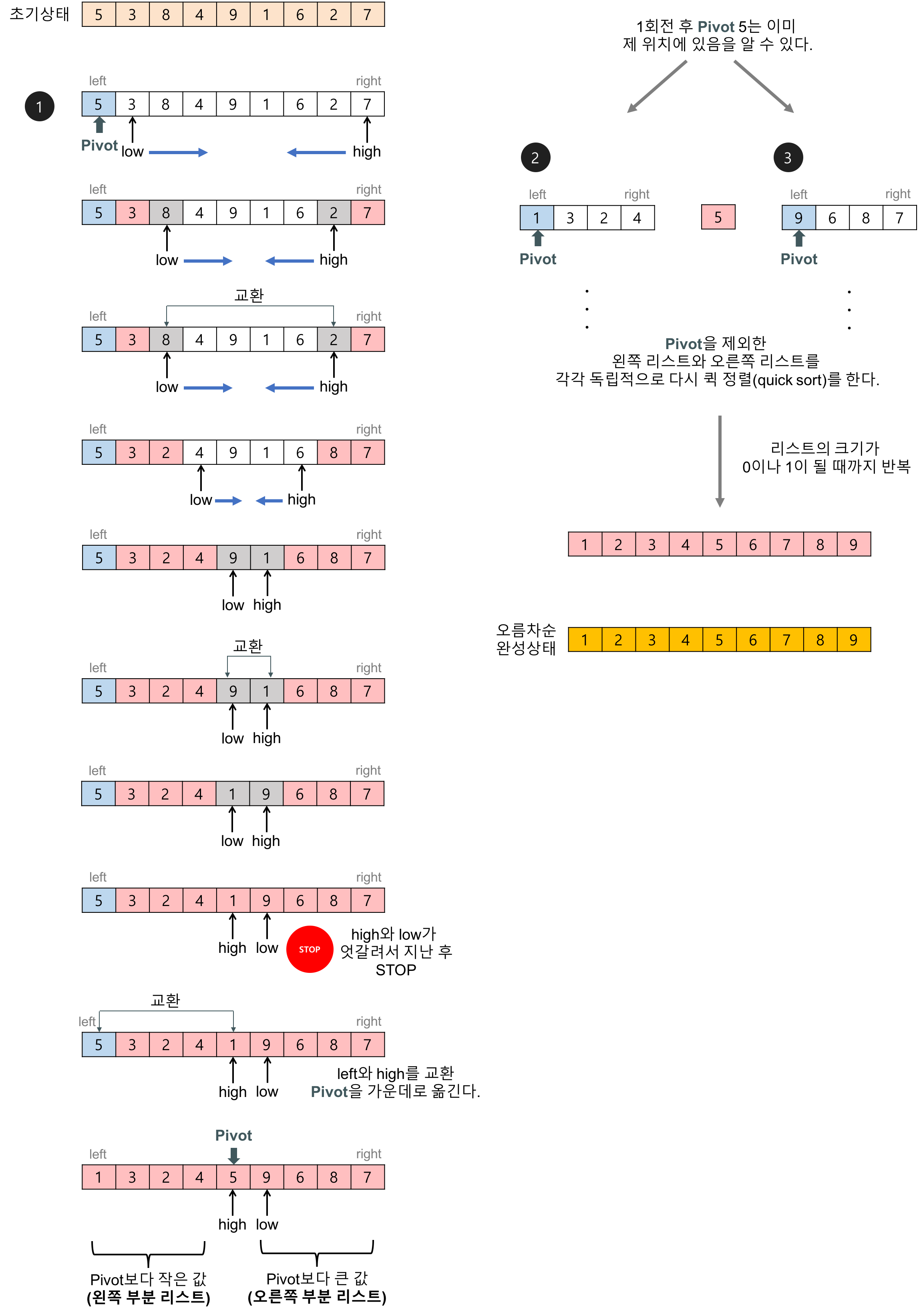
퀵 정렬 이란

퀵 정렬은 기준점을 획득한 다음 해당 기준점을 기준으로 배열을 나눈다. 한 쪽에는 기준점보다 작은 항목들이 위치하고 다른 쪽에는 기준점보다 큰 항목들이 위치한다. 나뉘어진 하위 배열에 대해 재귀적으로 퀵 정렬을 호출하여, 모든 배열이 기본 배열(요소가 하나뿐인 배열)이 될 때까지 반복하면 정렬이 완료된다.

❓ 퀵정렬이 정렬중에 가장 빠른 알고리즘으로 알려져 있는데 모든 상황에서 유리할까?

예시 ) 정렬되어 있는 경우를 또 정렬하는 경우[1,2,3,4] 인 배열이 있을 때 1을 기준점으로 두고 두 개의 부분배열로 나누면 4번의 연산이 필요하다. 현재 1보다 작은 배열은 없는 상태이고 큰 배열엔 [2,3,4]가 있으므로 [2,3,4]를 또 나누면 3번의 연산이 필요 ...이렇게 총 4+3+2+1로 O(n^2)의 시간복잡도를 갖게 된다.

👉 이러한 경우 퀵 정렬보다 삽입 정렬이 빠르다.

자바 스크립트 알고리즘

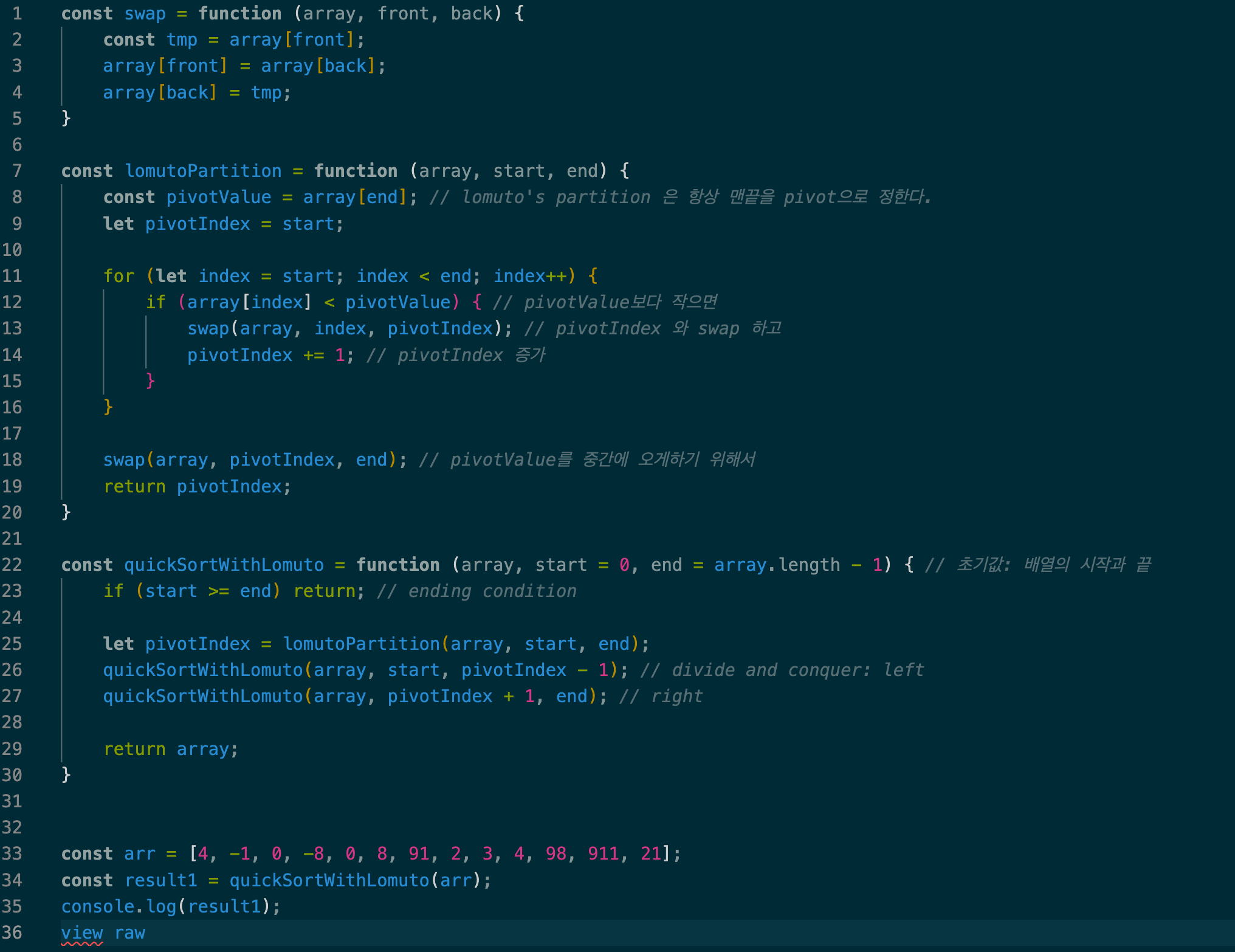
자바 알고리즘

public class QuickSorter {
    public static List<Integer> quickSort(List<Integer> list) {
        if (list.size() <= 1) return list;
        int pivot = list.get(list.size() / 2);

        List<Integer> lesserArr = new LinkedList<>();
        List<Integer> equalArr = new LinkedList<>();
        List<Integer> greaterArr = new LinkedList<>();

        for (int num : list) {
            if (num < pivot) lesserArr.add(num);
            else if (num > pivot) greaterArr.add(num);
            else equalArr.add(num);
        }

        return Stream.of(quickSort(lesserArr), equalArr, quickSort(greaterArr))
                .flatMap(Collection::stream)
                .collect(Collectors.toList());
    }
}