[알고리즘] Prim's algorithm

SeongWon Oh·2021년 9월 24일
MSTMinimum Spanning TreePrim's algorithmtree알고리즘최소 신장 트리
0

알고리즘

목록 보기
12/12
post-thumbnail

최소 신장 트리

  • Spanning Tree(신장 트리)란 Cycle이 없지만 모든 node들이 연결되어있는 그래프를 의미한다.
  • Spanning Tree가 되기 위한 조건은 Tree가 그래프의 모든 node들을 포함하며 Tree의 속성인 Cycle이 없음을 만족해야한다.
  • 아래의 사진은 Spanning Tree의 예시를 나타낸 사진이다.
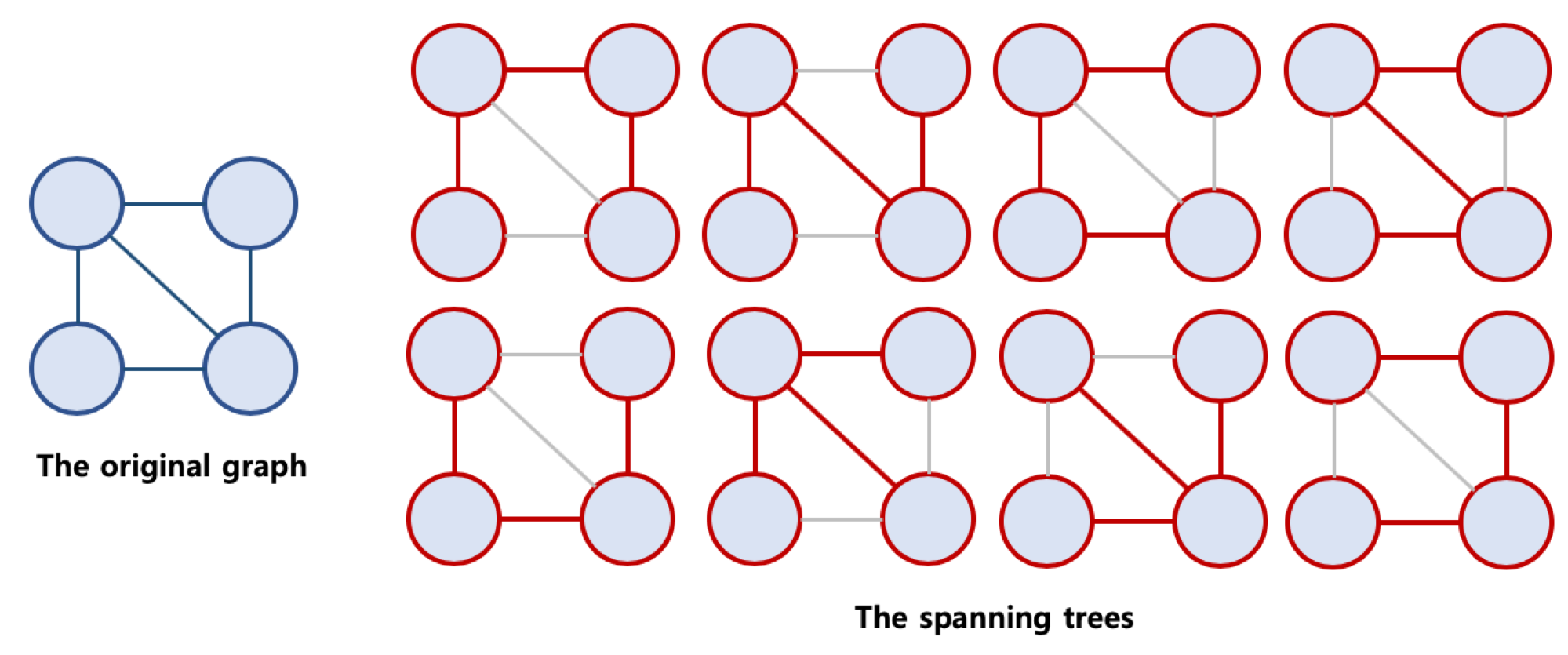
  • Minimun Spanning Tree(MST, 최소 신장 트리)는 Spanning Tree중에서 Edge(간선)의 가중치의 합이 최소인 Spanning Tree를 의미한다.
    • 대표적인 알고리즘으로는 Kruskal’s algorithm (크루스칼 알고리즘), Prim's algorithm (프림 알고리즘)이 있다.

Prim's algorithm

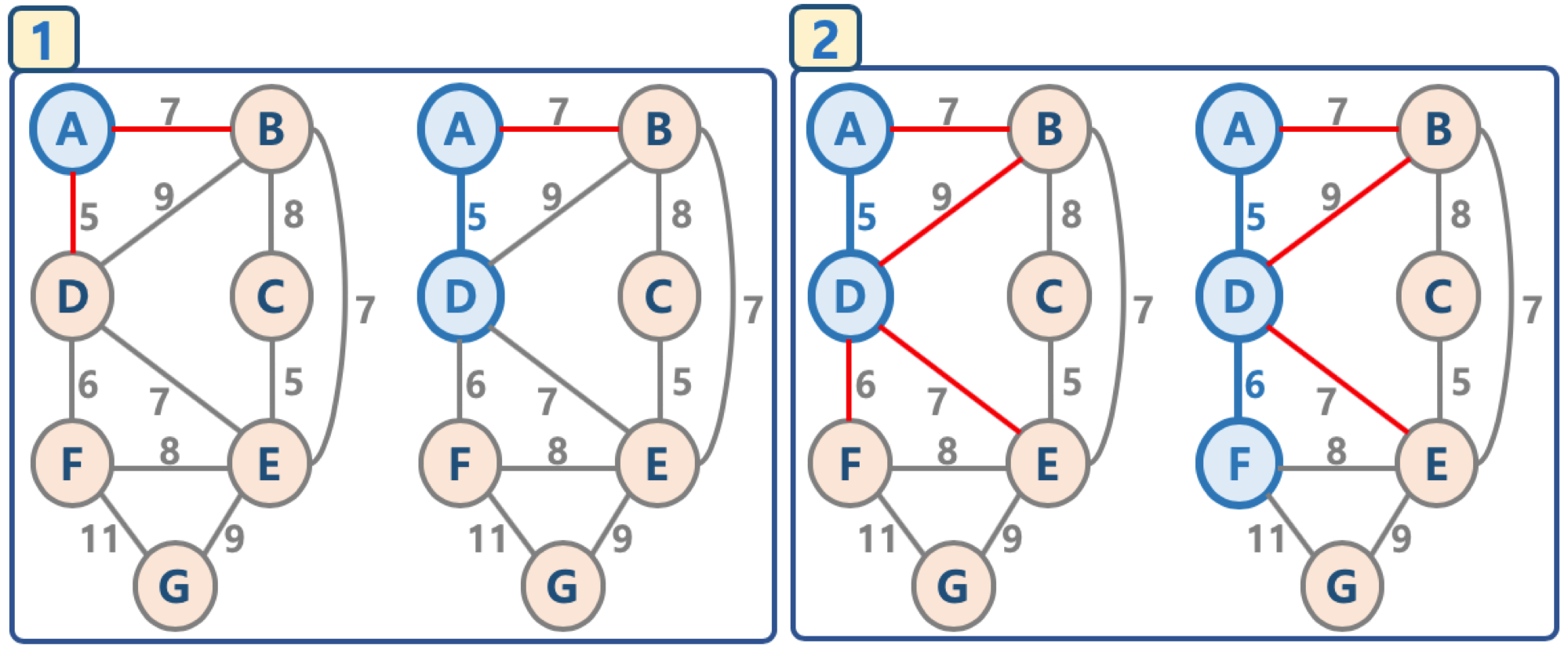
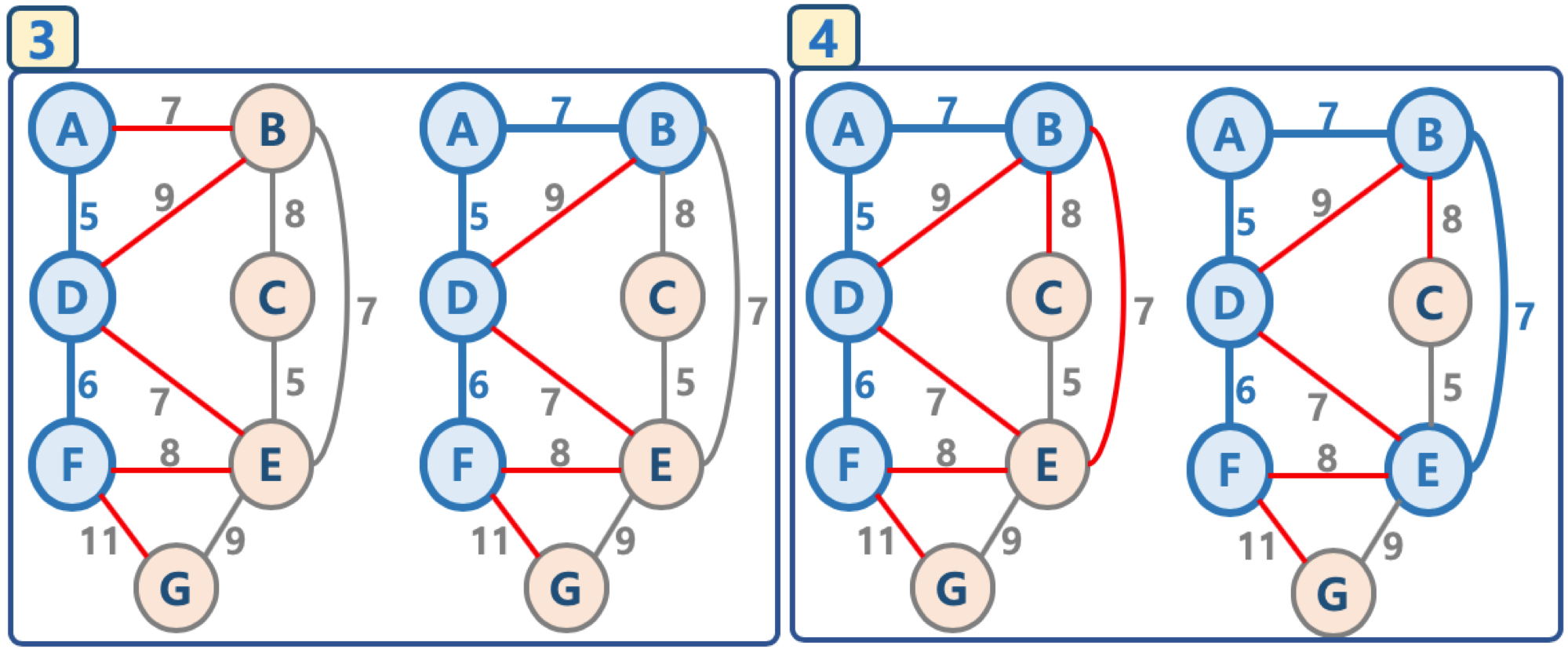
  • 프림 알고리즘은 시작 Node를 선택한 후, 해당 Node에 연결된 가중치가 가장 작은 edge에 연결된 node를 cycle이 생기지 않는다면 연결하고, 다시 연결되어진 node들에 연결되어 있는 edge중에서 가장 가중치가 작은 edge를 찾는 방법을 반복하며 진행된다.
  • 순서
    1. 임의의 node를 선택 후, 연결된 노드를 담는 집합에 해당 node를 넣는다.
    2. 새로 추가된 node에 연결된 edge들을 candidate edge리스트에 삽입
    3. edge 리스트에서 가장 작은 가중치를 가지는 간선부터 추출해서,
    3.1. 해당 edge에 연결된 인접 node가 '연결된 노드 집합'에 이미 들어 있다면, 스킵하며
    3.2. 해당 edge에 연결된 인접 node가 '연결된 노드 집합'에 들어 있지 않으면, 해당 edge를 선택하고, 해당 edge를 연결한다.
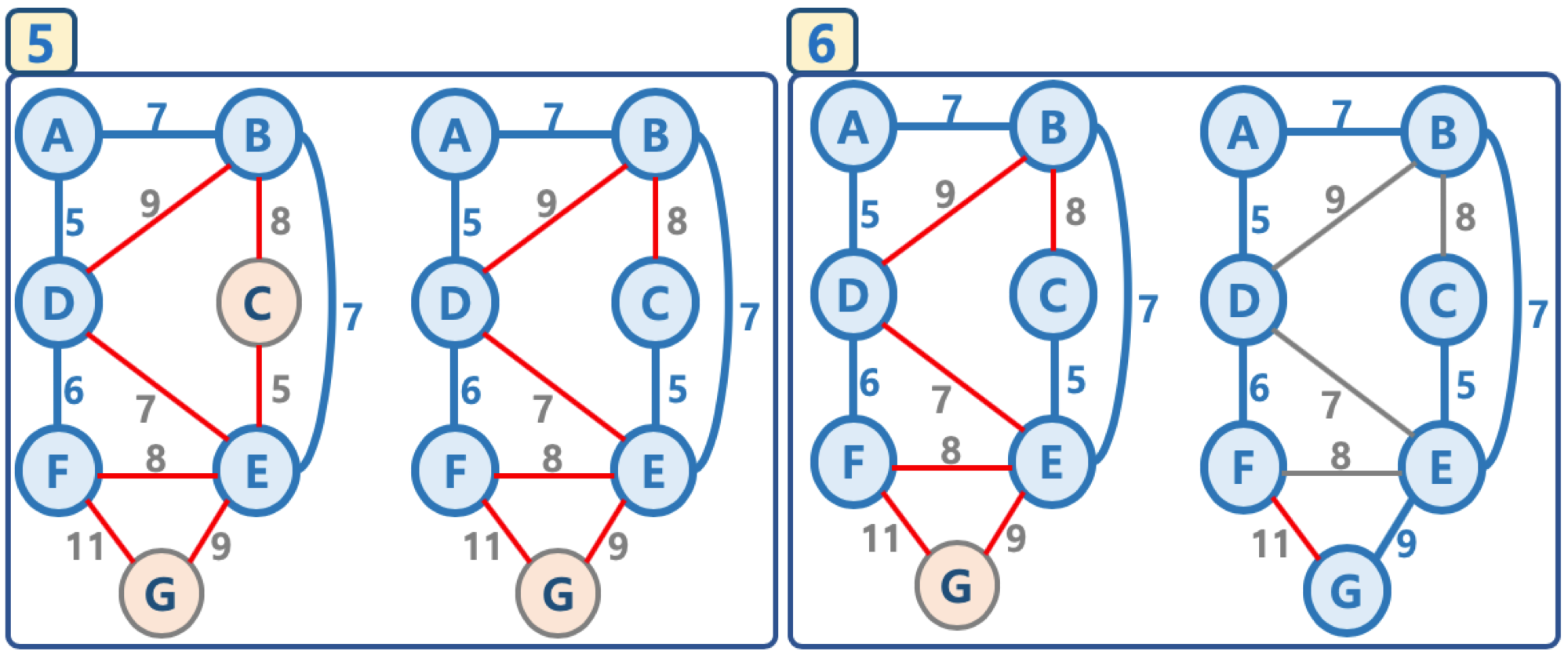
    4. 간선 리스트에 더 이상의 간선이 없을 때까지 2-3번을 반복한다.
  • 시간 복잡도는 최악의 경우 while문에서 모든 edge에 대해 반복을 해야하며 min heap구조를 사용하여 O(ElogE)O(ElogE)의 시간 복잡도를 갖는다.



Kruskal’s algorithm과 Prim's algorithm비교

  • 공통점: 둘 다 Greedy algorithm을 기초로 하며 결과적으로는 최적의 솔루션을 찾는다.
  • 차이점
    • Kruskal's algorithm은 전체 Edge를 보며 가중치가 적은 edge부터 연결하면서 MST를 구한다.
    • Prim's algorithm은 특정 node에서 시작하여 현재 연결되어 있는 edge들에 대해서 가장 작은 가중치가 작은 edge를 연결해가며 MST를 찾는다.

👨🏻‍💻 Prim's algorithm 구현 (Edge기준)

package algorithm;
import java.util.*;
public class Prim {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		char[] vertices = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};

		ArrayList<Edge> edges = new ArrayList<>();
		edges.add(new Edge(7, 'A', 'B'));
		edges.add(new Edge(5, 'A', 'D'));
		edges.add(new Edge(7, 'B', 'A'));
		edges.add(new Edge(8, 'B', 'C'));
		edges.add(new Edge(9, 'B', 'D'));
		edges.add(new Edge(7, 'B', 'E'));
		edges.add(new Edge(8, 'C', 'B'));
		edges.add(new Edge(5, 'C', 'E'));
		edges.add(new Edge(5, 'D', 'A'));
		edges.add(new Edge(9, 'D', 'B'));
		edges.add(new Edge(7, 'D', 'E'));
		edges.add(new Edge(6, 'D', 'F'));
		edges.add(new Edge(7, 'E', 'B'));
		edges.add(new Edge(5, 'E', 'C'));
		edges.add(new Edge(7, 'E', 'D'));
		edges.add(new Edge(8, 'E', 'F'));
		edges.add(new Edge(9, 'E', 'G'));
		edges.add(new Edge(6, 'F', 'D'));
		edges.add(new Edge(8, 'F', 'E'));
		edges.add(new Edge(11, 'F', 'G'));
		edges.add(new Edge(9, 'G', 'E'));
		edges.add(new Edge(11, 'G', 'F'));
		
		prim('A' ,vertices, edges);
	}
	
	public static ArrayList<Edge> prim(char start, char[] vertices, ArrayList<Edge> edges) {
		ArrayList<Edge> mst = new ArrayList<>();
		
		// 각각 node에 연결된 edge들을 저장
		HashMap<Character, ArrayList<Edge>> adjacentEdges = new HashMap<>();
		for (char v : vertices) {
			adjacentEdges.put(v, new ArrayList<Edge>());
		}
		for (Edge e: edges) {
			adjacentEdges.get(e.node1).add(e);
		}

		
		// 현재 연결된 Node의 Set
		HashSet<Character> connectedNode = new HashSet<Character>();
		connectedNode.add(start);
		
		// 연결딘 Node Set에 연결되어 있는 edge들
		PriorityQueue<Edge> candidateEdge = new PriorityQueue<>();
		candidateEdge.addAll(adjacentEdges.get(start));
		
		Edge temp;
		while (!candidateEdge.isEmpty()) {
			// candidateEdge에 값이 있을 경우 계속 실행되며
			// 연결된 edge중에서 weight이 가장 작은 edge를 연결을 시도하는데
			// 해당 edge의 끝 점에 연결된 node가 현재 연결된 node에 없으면 연결하고
			// 연결된 node에 해당 node가 이미 속해있다면 pass한다.
			temp = candidateEdge.poll(); 
			if (!connectedNode.contains(temp.node2)) {
				connectedNode.add(temp.node2);
				mst.add(temp);
				System.out.println(temp.weight + ", " + temp.node1 + ", " + temp.node2);		
			}
			for (Edge e : adjacentEdges.get(temp.node2)) {
				if (!connectedNode.contains(e.node2)) {
					candidateEdge.add(e);
				}			
			}
		}
		return mst;
		
	}
	

}

class Edge implements Comparable<Edge> {
	int weight;
	char node1;
	char node2;
	
	public Edge(int weight, char node1, char node2) {
		this.weight = weight;
		this.node1 = node1;
		this.node2 = node2;
	}
	
	@Override
	public int compareTo(Edge o) {
		// TODO Auto-generated method stub
		return this.weight < o.weight? -1:1;
	}
}

개선된 Prim's algorithm (Node기준)

  • 위에서 설명하고 구현한 Prim's algorithm의 경우 Edge를 기준으로 했다면 개선된 Prim's algorithm의 경우는 Node를 기준으로 한다.
  • 순서
    1. 시작점의 Node의 value는 0, 그 외의 Node의 value는 무한대로 설정해두고 List에 저장을 한다.
    1. List를 정렬한 후 value값이 가장 적은 node를 뽑는다.(뽑은 node는 list에서 제거)
    2. 뽑은 node에 연결된 edge들의 weight을 연결 하였을 때 연결된 node의 weight을 줄일 수 있다면 해당 edge를 연결하며 edge의 weight이 node의 weight보다 클 경우 업데이트를 하지 않는다.
    3. Node를 담은 list가 빌 때까지 2-3을 반복한다.
  • Node를 기준으로 구현한 Prim's algorithm의 시간복잡도는 O(ElogV)O(ElogV)이다.

👨🏻‍💻 개선된 Prim's algorithm 구현 (Node기준)

package algorithm;
import java.util.*;
public class Prim_improved {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		char[] vertices = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};

		ArrayList<Edge> edges = new ArrayList<>();
		edges.add(new Edge(7, 'A', 'B'));
		edges.add(new Edge(5, 'A', 'D'));
		edges.add(new Edge(7, 'B', 'A'));
		edges.add(new Edge(8, 'B', 'C'));
		edges.add(new Edge(9, 'B', 'D'));
		edges.add(new Edge(7, 'B', 'E'));
		edges.add(new Edge(8, 'C', 'B'));
		edges.add(new Edge(5, 'C', 'E'));
		edges.add(new Edge(5, 'D', 'A'));
		edges.add(new Edge(9, 'D', 'B'));
		edges.add(new Edge(7, 'D', 'E'));
		edges.add(new Edge(6, 'D', 'F'));
		edges.add(new Edge(7, 'E', 'B'));
		edges.add(new Edge(5, 'E', 'C'));
		edges.add(new Edge(7, 'E', 'D'));
		edges.add(new Edge(8, 'E', 'F'));
		edges.add(new Edge(9, 'E', 'G'));
		edges.add(new Edge(6, 'F', 'D'));
		edges.add(new Edge(8, 'F', 'E'));
		edges.add(new Edge(11, 'F', 'G'));
		edges.add(new Edge(9, 'G', 'E'));
		edges.add(new Edge(11, 'G', 'F'));
		
		prim('A' ,vertices, edges);
	}
	
	public static ArrayList<Node> prim(char start, char[] vertices, ArrayList<Edge> edges) {
		ArrayList<Node> mst = new ArrayList<>();
		
		// 각각 node에 연결된 edge들을 저장
		HashMap<Character, ArrayList<Edge>> adjacentEdges = new HashMap<>();
		for (char v : vertices) {
			adjacentEdges.put(v, new ArrayList<Edge>());
		}
		for (Edge e: edges) {
			adjacentEdges.get(e.node1).add(e);
		}

		
		
		// node의 정보를 관리하는 Map 생성
		ArrayList<Node> nodeInfo = new ArrayList<>();
		for (char v : vertices) {
			if (v == start) {
				nodeInfo.add(new Node(v, 0));
				continue;
			}
			nodeInfo.add(new Node(v, 100));
		}
		
		
		Node temp;
		while (!nodeInfo.isEmpty()) {
			Collections.sort(nodeInfo);
			temp = nodeInfo.remove(0);
			mst.add(temp);
			System.out.println(temp.weight + ", " + temp.nodeId + ", " + temp.connectNode);
			
			for (Edge e: adjacentEdges.get(temp.nodeId)) {
				nodeInfo.forEach((value)-> {
					if ((value.nodeId == e.node2) && (value.weight > e.weight)) {
						value.weight = e.weight;
						value.connectNode = e.node1;
						//System.out.println("nodeId: "+value.nodeId +", node weight: "+ value.weight +", connected node: "+value.connectNode);
					}
				});
				
			}
			
		}
		return mst;
		
	}
	

}

class Edge implements Comparable<Edge> {
	int weight;
	char node1;
	char node2;
	
	public Edge(int weight, char node1, char node2) {
		this.weight = weight;
		this.node1 = node1;
		this.node2 = node2;
	}
	
	@Override
	public int compareTo(Edge o) {
		// TODO Auto-generated method stub
		return this.weight < o.weight? -1:1;
	}
}

class Node implements Comparable<Node>{
	char nodeId;
	int weight;
	char connectNode;
	
	public Node(char nodeId, int weight) {
		this.nodeId = nodeId;
		this.weight = weight;
	}
	
	@Override
	public int compareTo(Node o) {
		return this.weight < o.weight? -1:1;
	}
}

🔗 Reference

profile
SeongWon Oh
블로그 이전했습니다. -> https://seongwon.dev/
이전 포스트

[알고리즘] Kruskal's algorithm

0개의 댓글