[알고리즘] Kruskal's algorithm

SeongWon Oh·2021년 9월 23일

Kruskal's Algorithm MST Minimun Spanning Tree Spanning Tree tree 알고리즘 최소 신장 트리

알고리즘

목록 보기

11/12

최소 신장 트리

Spanning Tree(신장 트리)란 Cycle이 없지만 모든 node들이 연결되어있는 그래프를 의미한다.
Spanning Tree가 되기 위한 조건은 Tree가 그래프의 모든 node들을 포함하며 Tree의 속성인 Cycle이 없음을 만족해야한다.
아래의 사진은 Spanning Tree의 예시를 나타낸 사진이다.
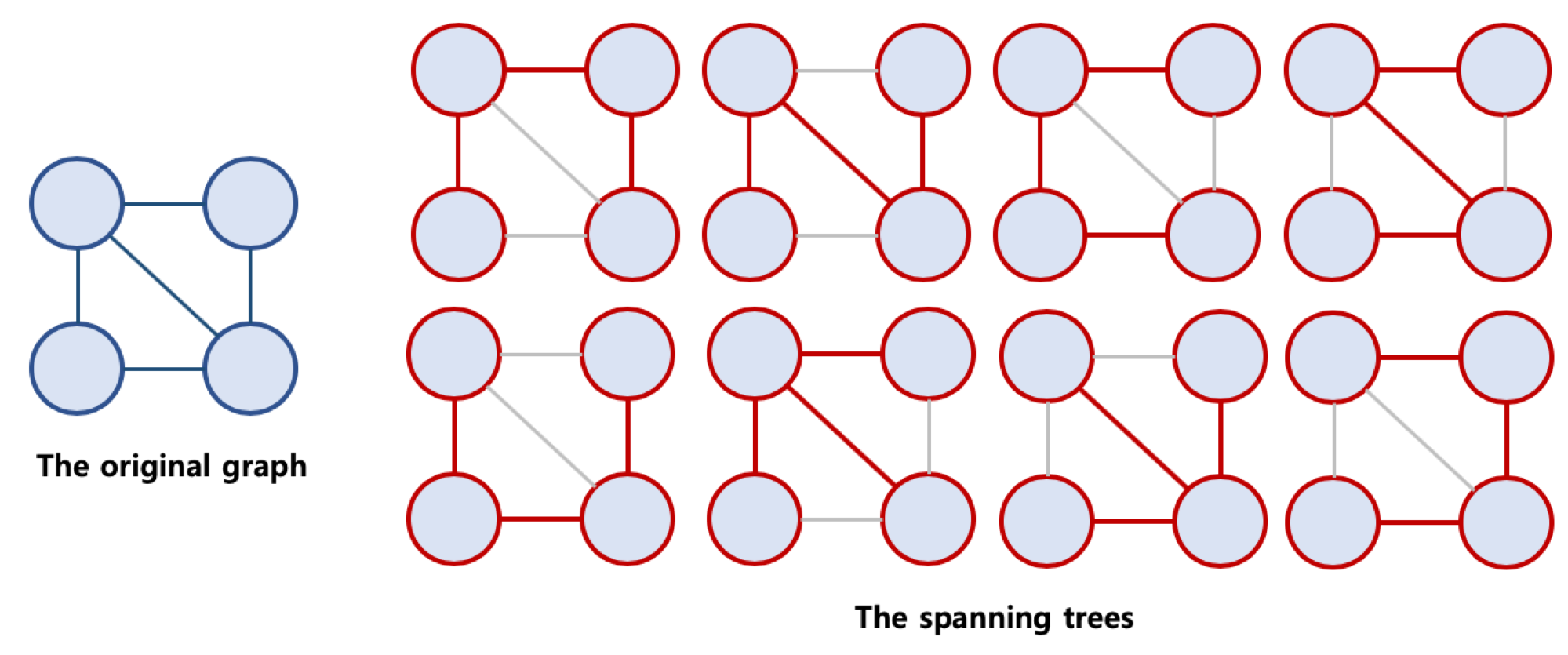
Minimun Spanning Tree(MST, 최소 신장 트리)는 Spanning Tree중에서 Edge(간선)의 가중치의 합이 최소인 Spanning Tree를 의미한다.
- 대표적인 알고리즘으로는 Kruskal’s algorithm (크루스칼 알고리즘), Prim's algorithm (프림 알고리즘)이 있다.

Kruskal's algorithm

Kruskal's algorithm은 대표적인 MST알고리즘으로 Edge를 가중치에 따라 정렬한 후 가중치가 낮은 Edge부터 cycle이 생기지 않는다면 연결하는 방법으로 진행된다.
전반적인 순서는 다음과 같다.
1. 모든 Node를 독립적인 집합으로 만든다.
1. 모든 Edge를 가중치 순으로 정렬후 가중치가 작은 Edge부터 연결된 node들을 비교한다.
2. Edge에 연결된 두 Node의 Root node를 비교하고 Root node가 서로 다를 경우 두개의 Node를 연결한다. (Root Node가 같으면 cycle이 생긴다고 판단하고 패스)
크루스칼 알고리즘은 전반적으로 Greedy algorithm을 기반으로 현재 가장 작은 가중치를 가진 edge를 선책하여 최적의 솔루션을 찾으려고 한다.
구현을 하기 위해서는 Edge들의 집합을 합치는 Union알고리즘과 node의 root node를 찾아내는 Find알고리즘이 필요하다.

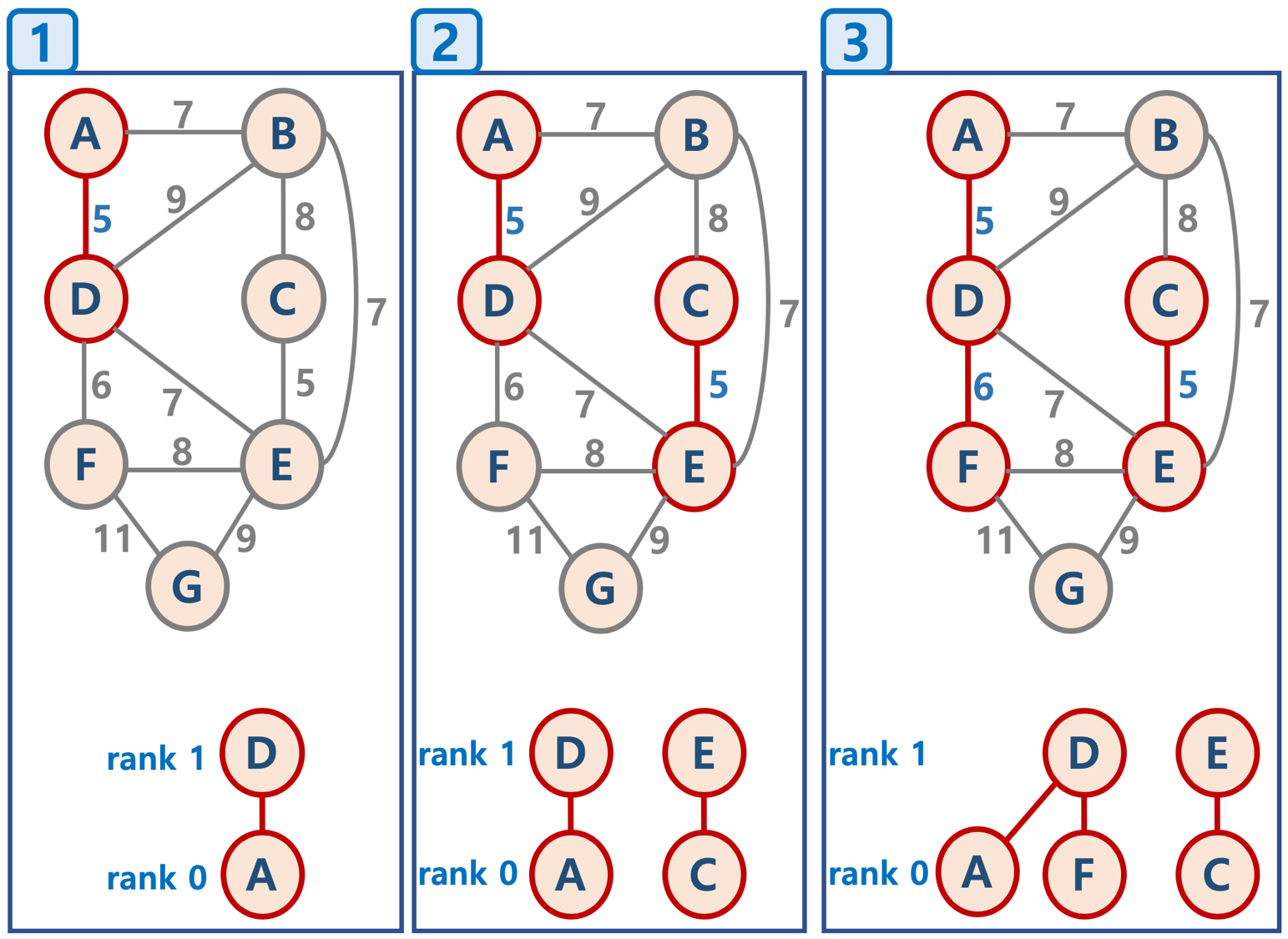
Union-Find Algorithm

구현을 하기 위해서는 Edge들의 집합을 합치는 Union알고리즘과 node의 root node를 찾아내는 Find알고리즘이 필요하다.
최악의 경우 링크드 리스트와 같은 형태가 되어 계산량이 O(N)이 될 수 있다. 이를 막기 위해 union-by-rank, path compression 기법을 사용한다.

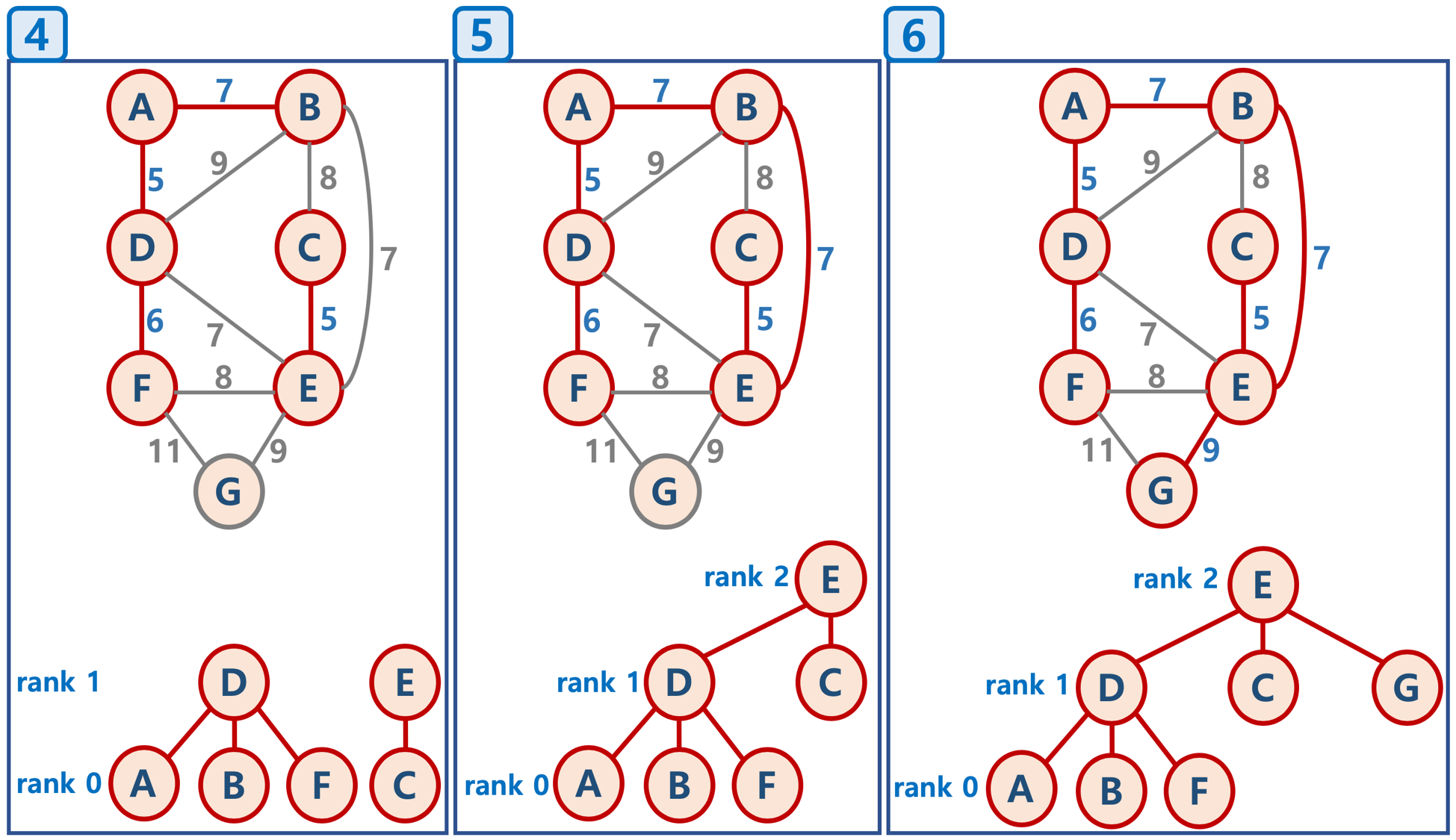
union-by-rank

두 Tree의 높이가 다를 경우 높이가 높은 Tree의 Root node에 낮은 Tree를 연결하여 하나의 Tree를 만든다.
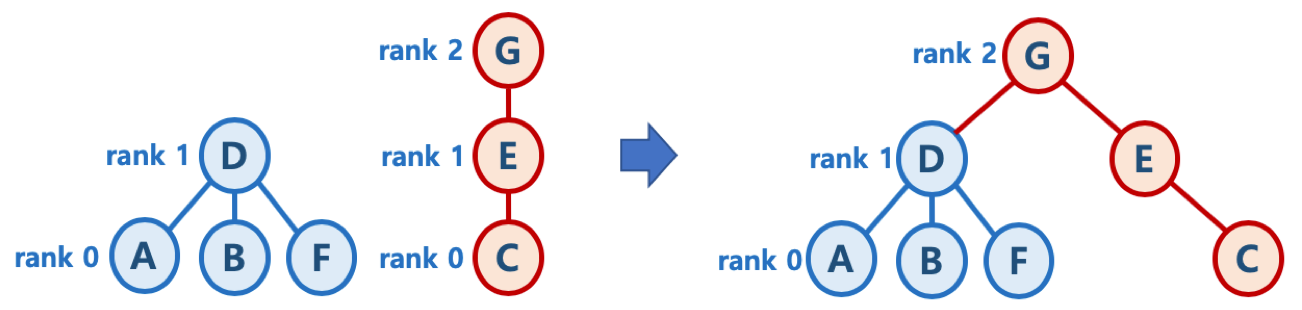
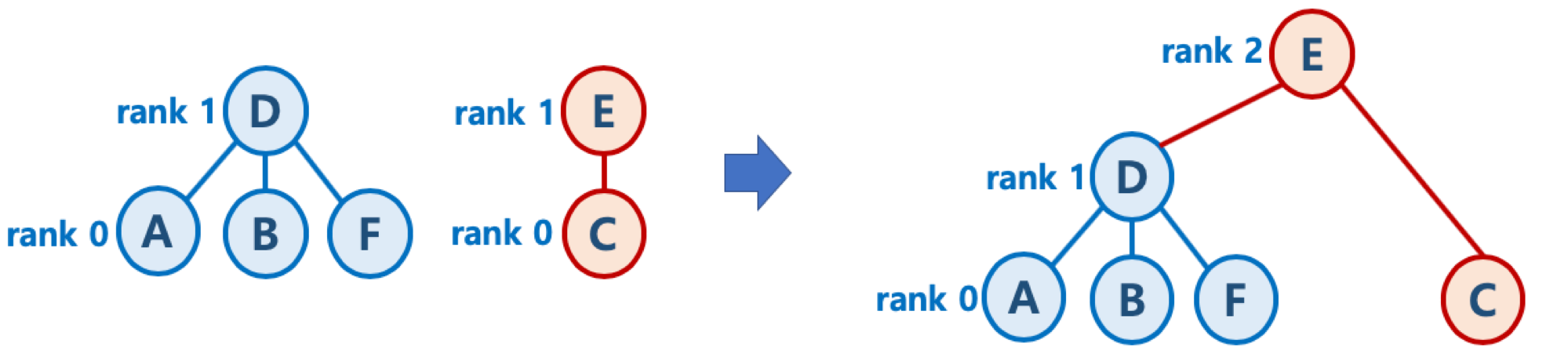
두 Tree의 높이가 같을 경우 한 쪽 Tree의 높이를 1 증가시켜준 후 다른 Tree를 붙여준다.

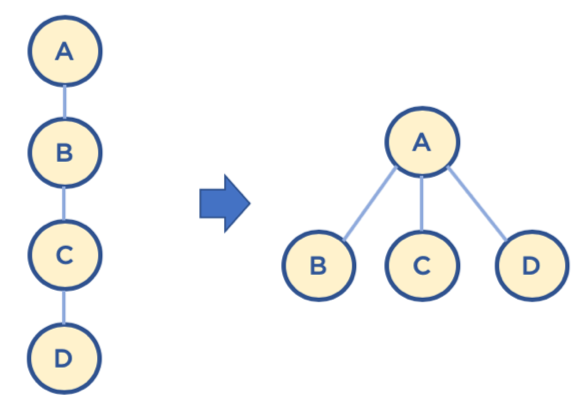
path compression

Find를 실행한 노드에서 거쳐간 노드를 루트에 다이렉트로 연결하는 기법이다.
Find를 실행한 노드는 이후부터는 루트 노드를 한번에 알 수 있다

시간 복잡도

크루스칼 알고리즘에서는 모든 Edge를 가중치를 기준으로 정렬하고 두 정점을 비교하게 되는데 이 경우 퀵소트를 사용한다면 시간복잡도는 $O(E logE)$ 가 된다.
각각 Root node를 확인 후 다를 경우 두 node를 연결하는데 union-by-rank 와 path compression 기법 사용시 시간 복잡도가 결국 상수값에 가까워 $O(1)$ 이 된다.
시간 복잡도는 가장 높은 수가 전체의 시간복잡도가 되어서 1,2중에서는 2번인 $O(E log E)$ 가 가장 커서 크루스컬 알고리즘의 시간 복잡도는 $O(E log E)$ 가 된다.

union-by-rank 와 path compression 기법 사용시 시간 복잡도는 다음 계산식을 만족함이 증명되었음

$O(M log^*{N})$

$log^*{N}$ 은 다음 값을 가짐이 증명되었음

N이 $2^{65536}$ 값을 가지더라도, $log^*{N}$ 의 값이 5의 값을 가지므로, 거의 $O(1)$ , 즉 상수값에 가깝다고 볼 수 있다

👨🏻‍💻 Kruskal's algorithm 구현

package algorithm;
import java.util.*;


public class Kruskal {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		char[] vertices = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
		// 각각 node들의 parent node들을 저장
		HashMap<Character, Character> parent = new HashMap<>();
		// 각 node들의 rank를 저장
		HashMap<Character, Integer> rank = new HashMap<>();
		for (char c:vertices) {
			parent.put(c, c);
			rank.put(c, 0);
		}
		
		
		PriorityQueue<Edge> edges = new PriorityQueue<>();
		edges.add(new Edge(7, 'A', 'B'));
		edges.add(new Edge(5, 'A', 'D'));
		edges.add(new Edge(7, 'B', 'A'));
		edges.add(new Edge(8, 'B', 'C'));
		edges.add(new Edge(9, 'B', 'D'));
		edges.add(new Edge(7, 'B', 'E'));
		edges.add(new Edge(8, 'C', 'B'));
		edges.add(new Edge(5, 'C', 'E'));
		edges.add(new Edge(5, 'D', 'A'));
		edges.add(new Edge(9, 'D', 'B'));
		edges.add(new Edge(7, 'D', 'E'));
		edges.add(new Edge(6, 'D', 'F'));
		edges.add(new Edge(7, 'E', 'B'));
		edges.add(new Edge(5, 'E', 'C'));
		edges.add(new Edge(7, 'E', 'D'));
		edges.add(new Edge(8, 'E', 'F'));
		edges.add(new Edge(9, 'E', 'G'));
		edges.add(new Edge(6, 'F', 'D'));
		edges.add(new Edge(8, 'F', 'E'));
		edges.add(new Edge(11, 'F', 'G'));
		edges.add(new Edge(9, 'G', 'E'));
		edges.add(new Edge(11, 'G', 'F'));
		
		kruskal(edges, rank, parent);
	}
	
	// 2개의 node들의 집합을 합침
	public static void union(char node1, char node2, HashMap<Character, Integer> rank, HashMap<Character, Character> parent) {
		if (rank.get(node1) > rank.get(node2)) {
			parent.put(node2, node1);
		}
		else {
			parent.put(node1, node2);
			if (rank.get(node1) == rank.get(node2)) {
				rank.put(node2, rank.get(node2)+1);
			}
		}

	}
	
	// Root node를 탐색
	public static char find(HashMap<Character, Character> parent, char n) {
		if (parent.get(n) != n)
			parent.put(n, find(parent, parent.get(n)));
		return parent.get(n);
		
	}
	
	public static ArrayList<Edge> kruskal(PriorityQueue<Edge> edges, HashMap<Character, Integer> rank, HashMap<Character, Character> parent) {
		ArrayList<Edge> result = new ArrayList<>();
		Edge temp;
		int len = edges.size();
		for (int i=0; i<len; i++) {
			temp = edges.poll();
			if (find(parent, temp.node1) != find(parent, temp.node2)) {
				union(find(parent, temp.node1), find(parent, temp.node2), rank, parent);
				result.add(temp);
				System.out.println(temp.weight+", "+temp.node1+", "+ temp.node2);

			}
		}
		return result;
	}

}


class Edge implements Comparable<Edge> {
	int weight;
	char node1;
	char node2;
	
	public Edge(int weight, char node1, char node2) {
		this.weight = weight;
		this.node1 = node1;
		this.node2 = node2;
	}
	
	@Override
	public int compareTo(Edge o) {
		// TODO Auto-generated method stub
		return this.weight < o.weight? -1:1;
	}
}