[게임 수학] 10. 미끄러짐 벡터(Sliding Vector)

🖥️ 미끄러짐 벡터(Sliding Vector)란?

충돌시 입사벡터가 입사면을 따라 미끄러지게 하기위해 수평성분만을 남긴 벡터이다.

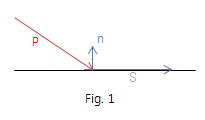
위 그림에서는 벡터P 가 법선벡터 n을 가진 입사면에 충돌했을 때, 미끄러짐 벡터 S를 확인할 수 있다.
미끄러짐 벡터S는 여러 방법으로 구할 수 있지만, 반사 벡터를 이용한 방법과 일반적인 방법 총 두 방법을 확인해보자.

반사 벡터를 이용한 방법

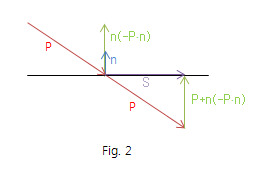
반사 벡터에서 입사벡터 P에 n(-P·n) 을 한 번 더해주면, 입사면에 투영된 접선벡터(Tangent Vector)를 구할 수 있다.
위 그림을 보면, 입사벡터의 역벡터 -P가 n에 투영된 n(-P·n)을 이용하여 슬라이딩벡터 S를 구할 수 있다.

그러므로 미끄러짐 벡터S는 S = P + n(-P·n) 으로 구할 수 있다.

일반적인 방법

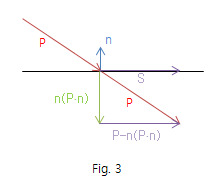
일반적인 방법은 입사벡터P 를 n에 바로 투영시키는 것이다.
입사벡터P 와 법선벡터n 의 끼인각이 0≤ θ ≤ π/2 일 때, P·n 의 값은 음수가 되므로, n벡터의 역벡터 방향으로 투영벡터가 생성된다.
이렇게 얻어진 투영벡터 n(P·n)을 입사벡터 P에서 빼주면, 미끄러짐 벡터S 를 얻을 수 있다.
그러므로 슬라이딩벡터 S 는 S = P - n(P·n)으로 구할 수 있다.

출처 :

• https://toymaker.tistory.com/entry/미끄러짐-벡터-Sliding-Vector