[데이터 분석과 통계] 통계가 중요한 이유, 기술통계와 추론통계, 다양한 분석 방법

📁 데이터 분석에 있어서 통계가 중요한 이유

<통계가 중요한 이유>

• 데이터를 분석하고 이를 바탕으로 결정을 내릴 수 있음
• 데이터 분석에서 통계는 데이터를 이해하고 해석하는 데 중요한 역할
• 데이터를 요약하고 패턴을 발견할 수 있음
• 추론을 통해 결론을 도출화는 과정을 도움
• 즉, 데이터 기반의 의사결정을 내릴 수 있음
• 결국 기업이 보다 현명한 결정을 내리고 수익을 창출하기 위해 필요
• 통계를 활용한 데이터 분석은 필수

<실제로 통계가 어떻게 사용되어 질까?>

• 고객 만족도 설문조사 분석

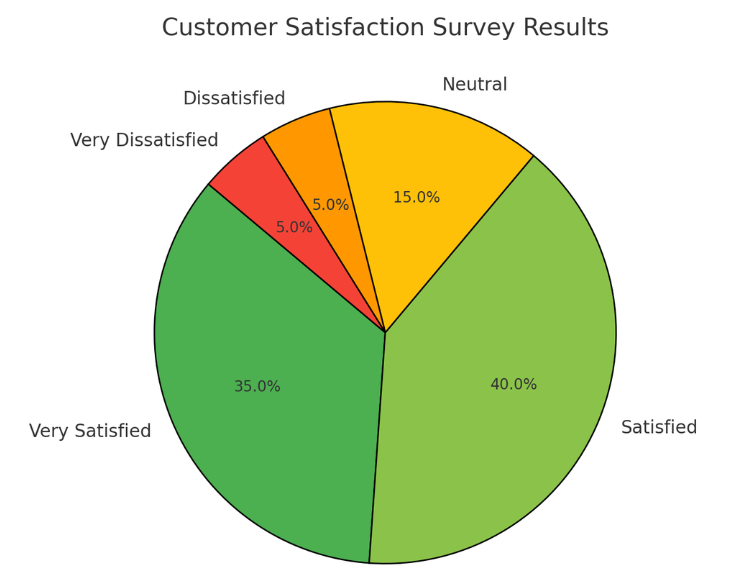
  • 설문 조사 중 고객의 불만 사항을 파악하고 이를 개선하는 데 활용할 수 있음
    

• 고객 유형별 세그먼트(Segment) 상품 추천

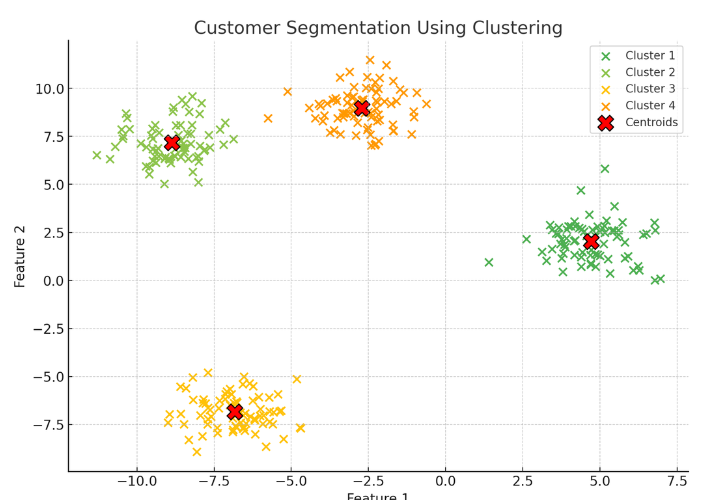
  • 고객을 유형별로 나누어 특징을 파악하고 각 유형에 맞는 상품을 추천하는데 활용될 수 있음
    

• 그 밖에도 다양한 상황에서 사용되어질 수 있음

  • 기업의 전략을 수립하기 위해서
  • 마케팅을 진행하기 위해서
  • 신제품을 개발하기 위해서 등등

📁 기술통계와 추론통계

1) 기술통계

• 데이터를 요약하고 설명하는 통계 방법
• 주로 평균, 중앙값, 분산, 표준편차 등을 사용
• 즉, 데이터를 특정 대표값으로 요약
• 데이터에 대한 대략적인 특징을 간단하고 쉽게 알 수 있음
• 단, 데이터 중 예외(이상치)라는게 항상 존재할 수 있고 데이터의 모든 부분을 확인할 수 있는 것은 아님
• ex) 사람을 처음 만날 때 그 사람의 전체에 대해서 다 알 수는 없지만 기본적인 인적사항들(외모, 직업, 학력, 나이, MBTI 등)로 대략적으로 그 사람에 대한 요약을 할 수 있는 것과 같음 → 하지만 여러분들도 알다시피 대략적으로 파악할 수는 있지만 그 사람에 대한 전부를 확인한 것은 아니며 예외가 항상 존재할 수 있음

💡 평균 (Mean)

• 평균은 데이터의 중앙값을 나타내는 값으로, 모든 데이터를 더한 후 데이터의 개수로 나누어 계산
• 이는 데이터의 일반적인 경향을 파악하는 데 유용
• ex) 다섯 명의 학생이 받은 시험 점수가 70, 80, 90, 100, 60이라면, 평균은 (70 + 80 + 90 + 100 + 60) / 5 = 80

💡 중앙값 (Median)

• 중앙값은 데이터셋을 크기 순서대로 정렬했을 때 중앙에 위치한 값
• 이는 이상치(예외적인 값들)에 영향을 덜 받기 때문에 데이터의 중심 경향을 나타내는 또 다른 방법
• 시험 점수가 60, 70, 80, 90, 100일 때, 중앙값은 80입니다. 만약 데이터가 짝수 개수라면, 중앙에 있는 두 값의 평균을 중앙값으로 함

💡 분산 (Variance)

• 분산은 데이터 값들이 평균으로부터 얼마나 떨어져 있는지를 나타내는 척도로, 데이터의 흩어짐 정도를 측정
• 분산이 크면 데이터가 넓게 퍼져 있고, 작으면 데이터가 평균에 가깝게 모여 있음을 의미
• 분산을 구하는 방법은 각 데이터 값에서 평균을 뺀 값을 제곱한 후, 이를 모두 더하고 데이터의 개수로 나누는 것
• ex) 네 명의 학생이 받은 시험 점수가 70, 80, 90, 100이라고 가정합시다. 이들의 평균은 (70 + 80 + 90 + 100) / 4 = 85
  → 각각의 데이터 값에서 평균을 뺀 값을 제곱하면?

(70 - 85)**2 = 225
(80 - 85)**2 = 25
(90 - 85)**2 = 25
(100 - 85)**2 = 225

→ 이 값을 모두 더한 후 데이터의 개수로 나누면, 분산 = (225 + 25 + 25 + 225) / 4 = 125가 됨

💡 표준편차 (Standard Deviation)

• 표준편차는 데이터 값들이 평균에서 얼마나 떨어져 있는지를 나타내는 통계적 척도로, 분산의 제곱근을 취하여 계산
• 표준편차는 데이터의 변동성을 측정하며, 값이 클수록 데이터가 평균으로부터 더 넓게 퍼져 있음을 의미
• ex) 네 명의 학생이 받은 시험 점수가 70, 80, 90, 100이라고 가정하면 이들의 평균은 85
  (70 - 85)^2 = 225
  (80 - 85)^2 = 25
  (90 - 85)^2 = 25
  (100 - 85)^2 = 225
  (여기까지는 분산 계산과 동일함)
  → 분산은 (225 + 25 + 25 + 225) / 4 = 125입니다. 표준편차는 분산의 제곱근이므로 분산에 루트(root)를 씌워 약 11.18

💡 표준편차와 분산의 관계

• 분산과 표준편차는 동일하게 데이터의 변동성을 측정하는 두 가지 주요 척도
• 두 개념은 밀접하게 연관되어 있으며, 표준편차는 분산의 제곱근
• 분산은 데이터 값과 평균의 차이를 제곱하여 평균을 낸 값이기 때문에 제곱 단위로 표현되지만, 표준편차는 다시 제곱근을 취하여 원래 데이터 값과 동일한 단위로 변환

2) 추론통계

• 표본 데이터를 통해 모집단의 특성을 추정하고 가설을 검정하는 통계 방법
• 주로 신뢰구간, 가설검정 등을 사용
• 즉, 데이터의 일부를 가지고 데이터 전체를 추정하는 것이 핵심
• ex) 비록 그 사람의 인생 전체를 다 본 것은 아니지만 대화를 진행하는 시간 동안 얻어낸 정보로 그 사람이 어떤 사람일지 알아가는 것과 같음

💡 신뢰구간 (Confidence Interval)

• 신뢰구간은 모집단의 평균이 특정 범위 내에 있을 것이라는 확률을 나타냄
• 일반적으로 95% 신뢰구간이 사용되며, 이는 모집단 평균이 95% 확률로 이 구간 내에 있음을 의미
• 만약 어떤 설문조사에서 평균 만족도가 75점이고, 신뢰구간이 70점에서 80점이라면, 우리는 95% 확률로 실제 평균 만족도가 이 범위 내에 있다고 말할 수 있음

💡 가설검정 (Hypothesis Testing)

• 가설검정은 모집단에 대한 가설을 검증하기 위해 사용됨
• 일반적으로 두 가지 가설이 있으며, 귀무가설(H0)은 검증하고자 하는 가설이 틀렸음을 나타내는 기본 가설(변화가 없다, 효과가 없다 등)이고, 대립가설(H1)은 그 반대 가설로 주장하는 바를 나타냄
• ex) 새로운 교육 프로그램이 학생들의 성적에 영향을 미치는지 알고 싶다면, 귀무가설은 "프로그램이 성적에 영향을 미치지 않는다"이고, 대립가설은 "프로그램이 성적에 영향을 미친다"임

3) 실제로 기술통계와 추론통계가 어떻게 사용되어 질까?

• 기술통계 : 회사의 매출 데이터를 요약하기 위해 평균 매출, 매출의 표준편차 등을 계산
• 추론통계 : - 일부 고객의 설문조사를 통해 전체 고객의 만족도를 추정

📁 다양한 분석 방법

1) 위치추정

• 데이터의 중심을 확인하는 방법!
• 평균, 중앙값이 대표적인 위치 추정 방법
• ex) 학생들의 시험 점수에서 평균 점수, 중간 점수를 계산
  (실습 전 라이브러리 호출)

# 데이터 분석에서 자주 사용되는 라이브러리
import pandas as pd
# 다양한 계산을 빠르게 수행하게 돕는 라이브러리
import numpy as np
# 시각화 라이브러리
import matplotlib.pyplot as plt
# 시각화 라이브러리2
import seaborn as sns

• 파이썬 실습

# 이 data는 아래에서도 계속 사용 됩니다
data = [85, 90, 78, 92, 88, 76, 95, 89, 84, 91]
mean = np.mean(data)
median = np.median(data)

print(f"평균: {mean}, 중앙값: {median}")

2) 변이추정

• 데이터들이 서로 얼마나 다른지 확인하는 방법!
• 분산, 표준편차, 범위(range) 등을 사용

💡 범위

• 범위는 데이터셋에서 가장 큰 값과 가장 작은 값의 차이를 나타내는 간단한 분포의 측도
• 범위를 통해 데이터가 어느 정도의 변동성을 가지는지 쉽게 파악할 수 있음
• 범위는 계산이 간단하여 기본적인 데이터 분석에서 자주 사용됨
  ↓
  <수식>
  범위(R) = 최대값 - 최소값
• ex) 다섯 명의 학생이 받은 시험 점수가 60, 70, 80, 90, 100이라고 가정
  최대값은 100
  최소값은 60
  → 따라서 범위는 100 - 60 = 40
• ex) 매출 데이터의 변이를 분석하여 비즈니스의 안정성을 평가
• 파이썬 실습

variance = np.var(data)
std_dev = np.std(data)
data_range = np.max(data) - np.min(data)

print(f"분산: {variance}, 표준편차: {std_dev}, 범위: {data_range}")

3) 데이터 분포 탐색

• 데이터의 값들이 어떻게 이루어져 있는지 확인하기
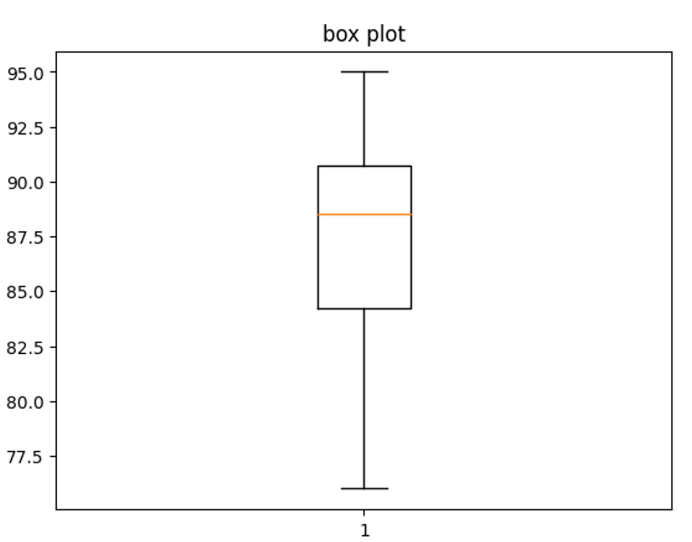
• 히스토그램과 상자 그림(Box plot)은 데이터의 분포를 시각적으로 표현하는 대표적인 방법
• ex) 시험 점수의 분포를 히스토그램과 상자 그림으로 표현
• 파이썬 실습

plt.hist(data, bins=5)
plt.title('histogram')
plt.show()

plt.boxplot(data)
plt.title('boxplot')
plt.show()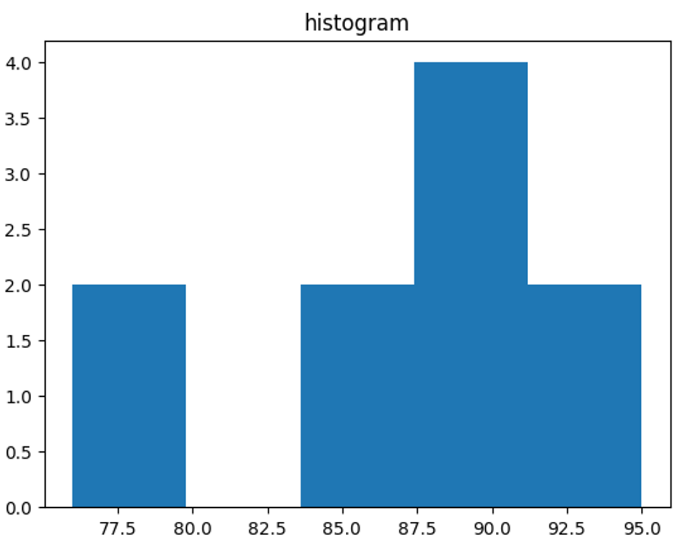

4) 이진 데이터와 범주 데이터 탐색

• 데이터들이 서로 얼마나 다른지 확인하는 방법!
• 최빈값(개수가 제일 많은 값)을 주로 사용
• 파이그림과 막대 그래프는 이진 데이터와 범주 데이터의 분포를 표현하는 대표적 방법
• ex) 고객 만족도 설문에서 만족/불만족의 빈도 분석
• 파이썬 실습

satisfaction = ['satisfaction', 'satisfaction', 'dissatisfaction', 
'satisfaction', 'dissatisfaction', 'satisfaction', 'satisfaction', 
'dissatisfaction', 'satisfaction', 'dissatisfaction']
satisfaction_counts = pd.Series(satisfaction).value_counts()

satisfaction_counts.plot(kind='bar')
plt.title('satisfaction distribution')
plt.show()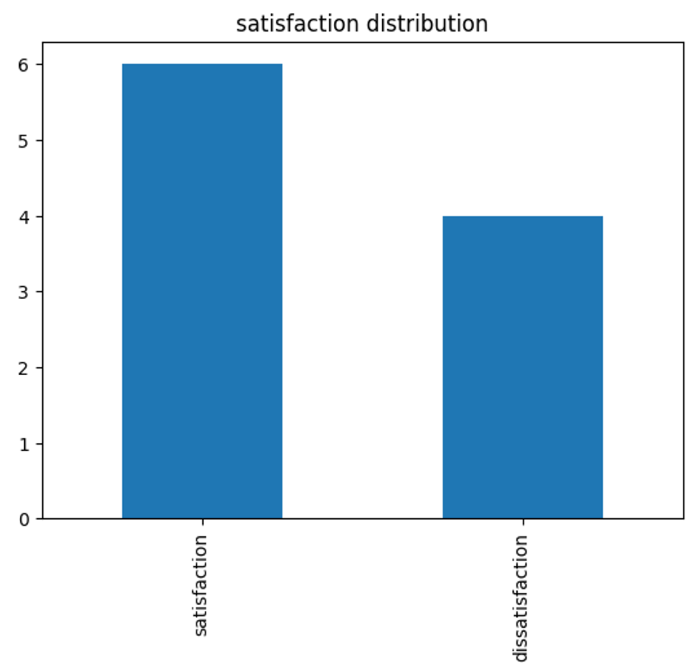

5) 상관관계

• 데이터들끼리 서로 관련이 있는지 확인하는 방법!
• 상관계수는 두 변수 간의 관계를 측정하는 방법
• 상관계수를 계산해서 -1이나 1에 가까워지면 강력한 상관관계를 가짐
• -0.5나 0.5를 가지면 중간정도의 상관관계를 가짐
• 0에 가까울 수록 상관관계가 없음
  
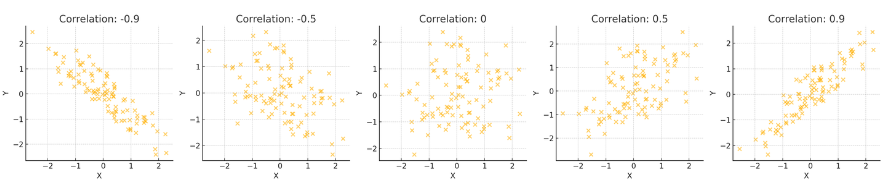
• ex) 공부 시간과 시험 점수 간의 상관관계를 분석
• 파이썬 실습

study_hours = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
exam_scores = [95, 90, 85, 80, 75, 70, 65, 60, 55, 50]
correlation = np.corrcoef(study_hours, exam_scores)[0, 1]

print(f"공부 시간과 시험 점수 간의 상관계수: {correlation}")

plt.scatter(study_hours, exam_scores)
plt.show()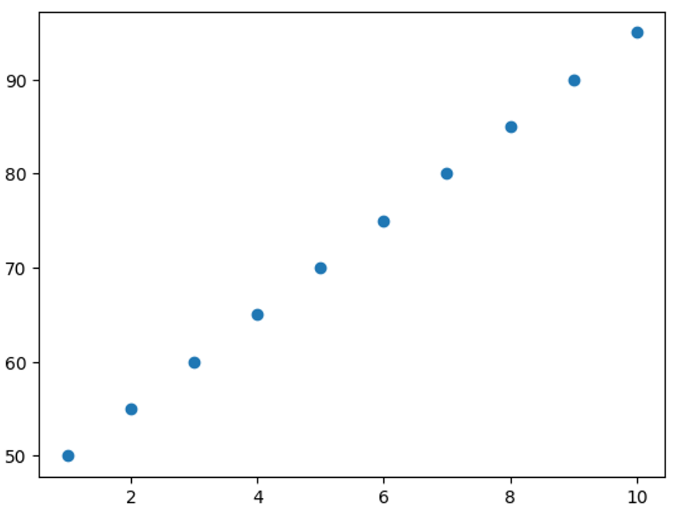

6) 인과관계와 상관관계의 차이

☑️ 인과관계는 상관관계와는 다르게 원인, 결과가 분명해야 함!

• 상관관계는 두 변수 간의 관계를 나타내며, 인과관계는 한 변수가 다른 변수에 미치는 영향을 나타냄
• ex) 아이스크림 판매량과 익사 사고 수 간의 상관관계는 높지만, 인과관계는 아님

7) 두 개 이상의 변수 탐색

• 다변량 분석은 여러 변수 간의 관계를 분석하는 방법
• ex) 여러 마케팅 채널의 광고비와 매출 간의 관계 분석
• 파이썬 실습

data = {'TV': [230.1, 44.5, 17.2, 151.5, 180.8],
        'Radio': [37.8, 39.3, 45.9, 41.3, 10.8],
        'Newspaper': [69.2, 45.1, 69.3, 58.5, 58.4],
        'Sales': [22.1, 10.4, 9.3, 18.5, 12.9]}
df = pd.DataFrame(data)

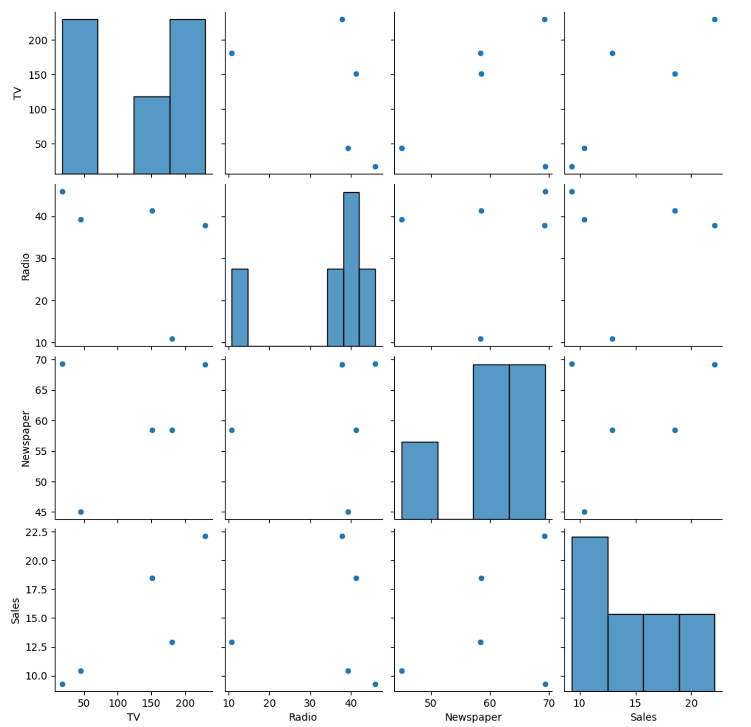
sns.pairplot(df)
plt.show()

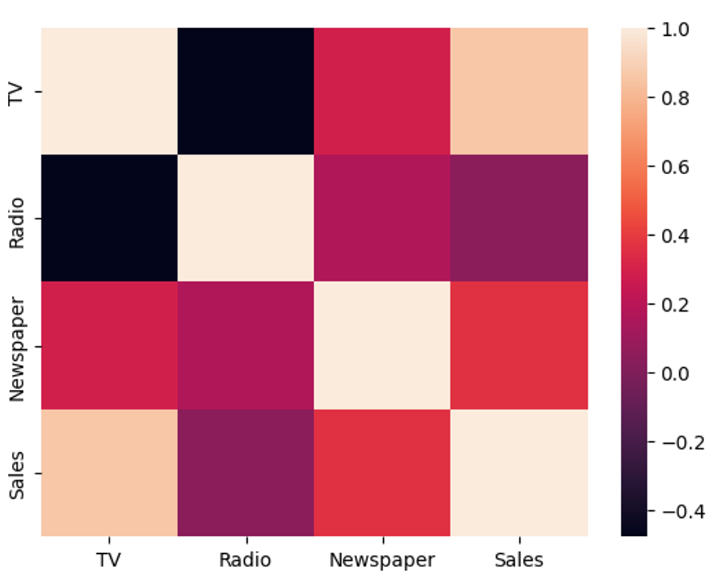
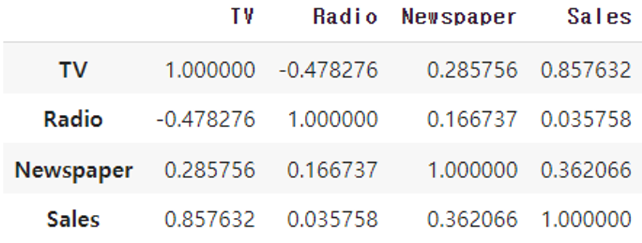
df.corr()

# heatmap까지 그린다면
sns.heatmap(df.corr())

< pairplot() >

• seaborn 라이브러리에서 제공하는 기능으로, 데이터셋의 각 변수(특성)들 간의 쌍(pair) 관계를 시각화하는 플롯
• 가능한 모든 변수 쌍에 대해 산점도(scatter plot)를 그려줌
  → 대각선 위치에는 각 변수의 분포를 보여주는 히스토그램이 표시
  

< corr() >

• 데이터 프레임의 각 변수(열) 간의 상관 관계를 계산하는 메서드
• 상관 계수 : 양의 값은 양의 상관 관계(하나가 증가하면 다른 하나도 증가하는 경향), 음의 값은 음의 상관 관계(하나가 증가하면 다른 하나는 감소하는 경향)
  

< heatmap >

• seaborn 또는 matplotlib 같은 시각화 라이브러리에서 제공하는 플롯으로, 데이터의 행렬 형태를 색상으로 나타내는 그래프
• 계산된 상관 계수 행렬을 시각화하는 데 사용