[통계] 모집단과 표본, 표본오차와 신뢰구간

📁 모집단과 표본

<모집단>

• 관심의 대상이 되는 전체 집단
• ex) 한 국가의 모든 성인

<표본>

• 모집단에서 추출한 일부
• ex) 그 국가의 성인 중 일부를 조사
  
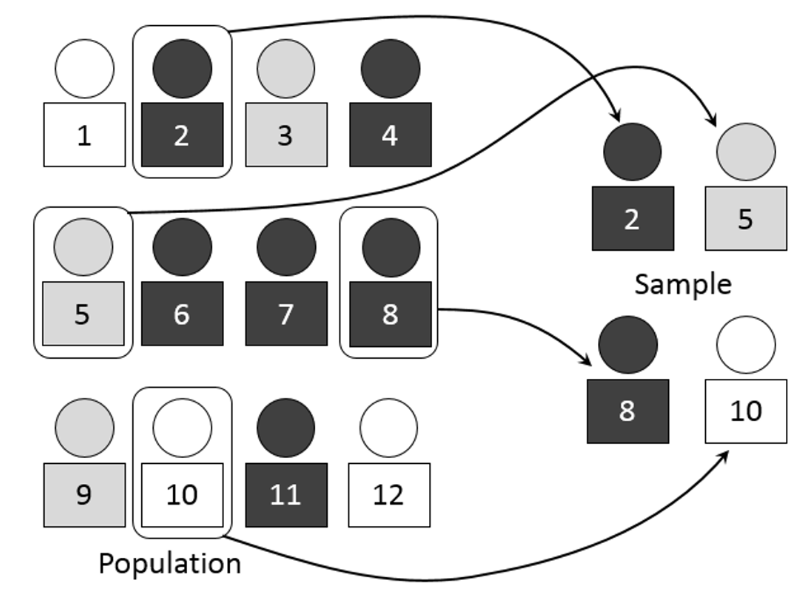
  -출처 : 위키백과-

<왜 표본을 사용하는 걸까?>

1) 현실적인 제약

• 비용과 시간

  • 전체 모집단을 조사하는 것은 비용과 시간이 많이 들기 때문에 대부분의 경우 불가능하거나 비효율적
  • 표본 조사는 이러한 자원을 절약하면서도 유의미한 결과를 도출할 수 있는 방법

• 접근성

  • 모든 데이터를 수집하는 것이 물리적으로 불가능한 경우가 많음
  • ex) 특정 질병에 걸린 모든 환자의 데이터를 수집하는 것은 어려울 수 있음

2) 대표성

• 잘 설계된 표본은 모집단의 특성을 반영할 수 있음
• 이를 통해 표본에서 얻은 결과를 모집단 전체에 일반화 가능
• 무작위로 표본을 추출하면 편향을 최소화하고 모집단의 다양한 특성을 포함할 수 있음

3) 데이터 관리

• 데이터 처리의 용이성

  • 표본 데이터를 사용하는 것은 전체 데이터를 다루는 것보다 데이터 처리와 분석이 훨씬 용이
  • 큰 데이터셋은 분석에 많은 컴퓨팅 자원이 필요할 수 있지만, 작은 표본은 이런 부담을 줄여줌

• 데이터 품질 관리

  • 작은 표본에서는 데이터 품질을 더 쉽게 관리하고, 오류나 이상값을 식별하여 수정할 수 있음

4) 모델 검증 용이

• 모델 적합도 테스트
  • 표본 데이터를 사용하여 통계적 모델을 검증할 수 있음
  • 모델이 표본 데이터에 잘 맞는다면, 모집단에도 잘 맞을 가능성이 높음

☑️ 전수조사

• 모집단 전체를 조사하는 방법. 대규모일 경우 비용과 시간이 많이 듦

☑️ 표본조사

• 표본만을 조사하는 방법(비용과 시간이 적게 들지만, 표본이 대표성을 가져야 함)

<실제로 어떻게 사용되어질까?>

• 실제로 모든 데이터를 다 수집할 수 없을 때 표본을 사용
  1) 도시 연구
• 한 도시의 모든 가구(모집단) 중 100가구(표본)를 조사하여 평균 전력 사용량을 추정

2) 의료 연구

• 특정 치료법의 효과를 알아보기 위해 전체 환자를 조사하는 대신, 표본을 통해 추정하고 이를 바탕으로 결론을 도출

3) 시장 조사

• 소비자 선호도를 파악하기 위해 모든 소비자를 조사하는 대신, 무작위로 선택된 표본을 통해 전체 시장의 트렌드를 추정

4) 정치 여론 조사

• 선거 전 여론 조사를 통해 전체 유권자의 투표 경향을 추정하여 선거 결과를 예측

ex)

import numpy as np
import matplotlib.pyplot as plt

# 모집단 생성 (예: 국가의 모든 성인의 키 데이터)
population = np.random.normal(170, 10, 1000)

# 표본 추출
sample = np.random.choice(population, 100)

plt.hist(population, bins=50, alpha=0.5, label='population', color='blue')
plt.hist(sample, bins=50, alpha=0.5, label='sample', color='red')
plt.legend()
plt.title('population and sample distribution')
plt.show()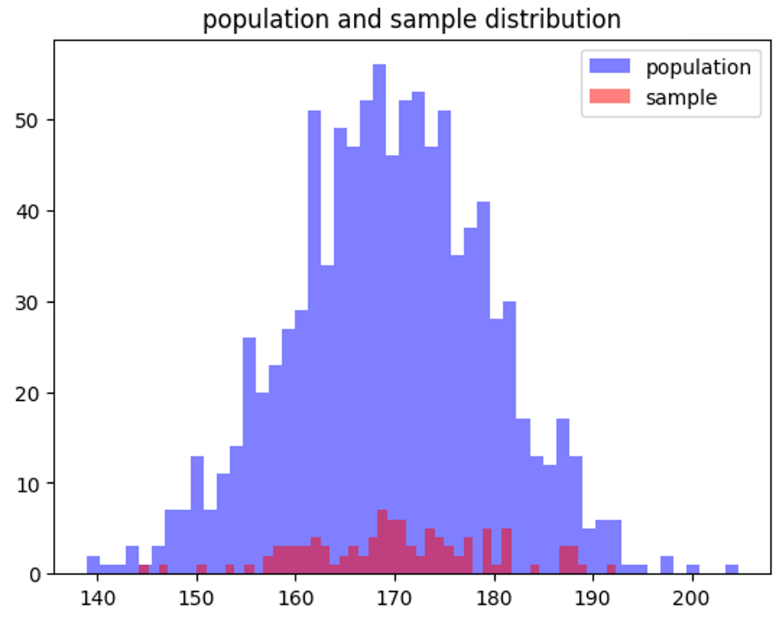

💡 numpy.random

• numpy.random
  • numpy.random 모듈은 NumPy 라이브러리의 일부
  • 다양한 확률 분포에 따라 난수를 생성하는 기능을 제공
  • 데이터 분석, 시뮬레이션 방법 등 다양한 분야에서 사용
• np.random.normal
  • 함수는 정규분포(가우시안 분포)를 따르는 난수를 생성
  • 정규분포는 평균과 표준편차를 중심으로 데이터가 대칭적으로 분포하는 분포
    ex)

numpy.random.normal(loc=0.0, scale=1.0, size=None)

→ loc (float): 정규분포의 평균 (기본값: 0.0)
→ scale (float): 정규분포의 표준편차 (기본값: 1.0)
→ size (int 또는 tuple of ints): 출력 배열의 크기 (기본값: None, 즉 스칼라 값 반환)

• np.random.choice
  • 주어진 배열에서 임의로 샘플링하여 요소를 선택
  • 이는 지정된 배열에서 무작위로 선택된 요소를 반환하는 기능을 제공
    ex)

numpy.random.choice(a, size=None, replace=True, p=None)

→ a (1-D array-like or int): 샘플링할 원본 배열. 정수인 경우 np.arange(a)와 동일하게 간주
→ size (int 또는 tuple of ints): 출력 배열의 크기 (기본값: None, 즉 단일 값 반환)
→ replace (boolean): 복원 추출 여부를 나타냄 / True면 동일한 요소가 여러 번 선택될 수 있음 (기본값: True)
→ p (1-D array-like, optional): 각 요소가 선택될 확률. 배열의 합은 1이어야 함

💡 plt.hist

• Matplotlib 라이브러리에서 히스토그램을 그리는 함수

• 히스토그램은 데이터의 분포를 시각화하는 데 유용한 도구

• bins

  • 히스토그램의 빈(bins)의 개수 또는 경계
  • 여기서 빈(bins)은 데이터 몇개의 구간으로 나눌 것인지에 대한 것
  • 정수나 리스트로 입력할 수 있음
    • 정수: 빈의 개수를 지정
    • 리스트: 각 빈의 경계를 직접 지정 (140~150, 150~160 … 이렇게 경계를 지정하고 싶으면 리스트로 작성)

• alpha

  • 히스토그램 막대의 투명도를 지정
  • 0(투명)에서 1(불투명) 사이의 값

• label

  • 히스토그램의 레이블을 지정
  • 여러 히스토그램을 그릴 때 범례를 추가하는 데 사용

• color

  • 히스토그램 막대의 색상을 지정

📁 표본오차와 신뢰구간

✔️ 표본이 모집단 대비해서 얼마나 차이나는지, 신뢰할 수 있는지 파악 가능!

1) 표본오차와 신뢰구간이란?

<표본오차 (Sampling Error)>

• 표본에서 계산된 통계량과 모집단의 진짜 값 간의 차이
• 표본 크기가 클수록 표본오차는 작아짐
• 이는 표본이 모집단을 완벽하게 대표하지 못하기 때문에 발생하며, 표본의 크기와 표본 추출 방법에 따라 달라질 수 있음
  • 표본의 크기 : 표본의 크기가 클수록 표본오차는 줄어듬 / 더 많은 데이터를 수집할수록 모집단을 더 잘 대표하게 됨
  • 표본 추출 방법 : 무작위 추출 방법을 사용하면 표본오차를 줄일 수 있음 / 모든 모집단 요소가 선택될 동등한 기회를 가지게 해야 함

<신뢰구간 (Confidence Interval)>

• 신뢰구간은 모집단의 특정 파라미터(예: 평균, 비율)에 대해 추정된 값이 포함될 것으로 기대되는 범위를 나타냄
• 신뢰구간 계산 방법
  • 신뢰구간=표본평균±z×표준오차
  • 여기서 z는 선택된 신뢰수준에 해당하는 z-값임
  • ex) 95% 신뢰수준의 z-값은 1.96
  • 일반적으로 95% 신뢰수준을 많이 사용

<표본오차, 신뢰구간 그림으로 확인>

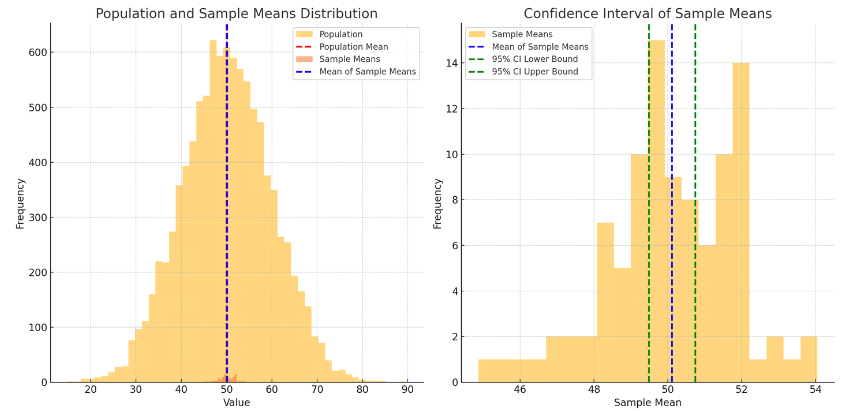
• 모집단과 표본 분포 (왼쪽 그림)
  • 붉은색 점선은 모집단의 평균
  • 파란색 점선은 표본의 평균
  • 모집단의 분포는 넓고, 표본 평균들의 분포는 좁아짐
  • 표본 크기가 커질수록 표본 평균이 모집단 평균에 더 가까워지는 경향을 보여줌
• 신뢰구간 시각화 (오른쪽 그림)
  • 오른쪽 그림은 표본의 분포와 95% 신뢰구간을 보여줌
  • 파란색 점선은 표본의 평균을 나타내고, 녹색 점선은 95% 신뢰구간의 상한과 하한을 나타냄
  • 이 신뢰구간은 모집단의 평균을 포함할 것으로 예상되는 범위

2) 실제로 어떻게 사용되어질까?

<수학점수 표본으로부터 모집단의 평균 범위를 계산해보자>

• 100명의 학생을 표본으로 추출하여 그들의 평균 수학 점수를 구하고, 이 점수의 신뢰구간을 계산

import scipy.stats as stats

# 표본 평균과 표본 표준편차 계산
sample_mean = np.mean(sample)
sample_std = np.std(sample)

# 95% 신뢰구간 계산
conf_interval = stats.t.interval(0.95, len(sample)-1, loc=sample_mean, scale=sample_std/np.sqrt(len(sample)))

print(f"표본 평균: {sample_mean}")
print(f"95% 신뢰구간: {conf_interval}")

💡 stats.t.interval

• scipy.stats는 SciPy 라이브러리의 일부로, 통계 분석을 위한 다양한 함수와 클래스들을 제공하는 모듈
• scipy.stats.t.interval 함수는 주어진 신뢰 수준에서 t-분포(밑에서 얘기하는 student t 분포)를 사용하여 신뢰 구간(confidence interval)을 계산하는 데 사용

scipy.stats.t.interval(alpha, df, loc=0, scale=1)

• alpha
  • 신뢰 수준(confidence level)을 의미
  • ex) 95% 신뢰 구간을 원하면 alpha를 0.95로 설정
• df
  • 자유도(degrees of freedom)를 나타냄
  • 일반적으로 표본 크기에서 1을 뺀 값으로 설정(df = n - 1)
• loc
  • 위치(parameter of location)로, 일반적으로 표본 평균을 설정
• scale
  • 스케일(parameter of scale)로, 일반적으로 표본 표준 오차(standard error)를 설정
  • 표본 표준 오차는 표본 표준편차를 표본 크기의 제곱근으로 나눈 값(scale = sample_std / sqrt(n))