이분 탐색이란?
이분 탐색(Binary Search)는 순차적 탐색보다 빠른 탐색을 위해 나온 방법으로, 정렬된 배열이나 리스트에서 필요한 값을 비교적 빠르게 찾을 수 있는 탐색 방법이다.
이분 탐색의 특징
-
검색할 배열이나 리스트는 반드시 정렬된 상태이어야 한다.
-
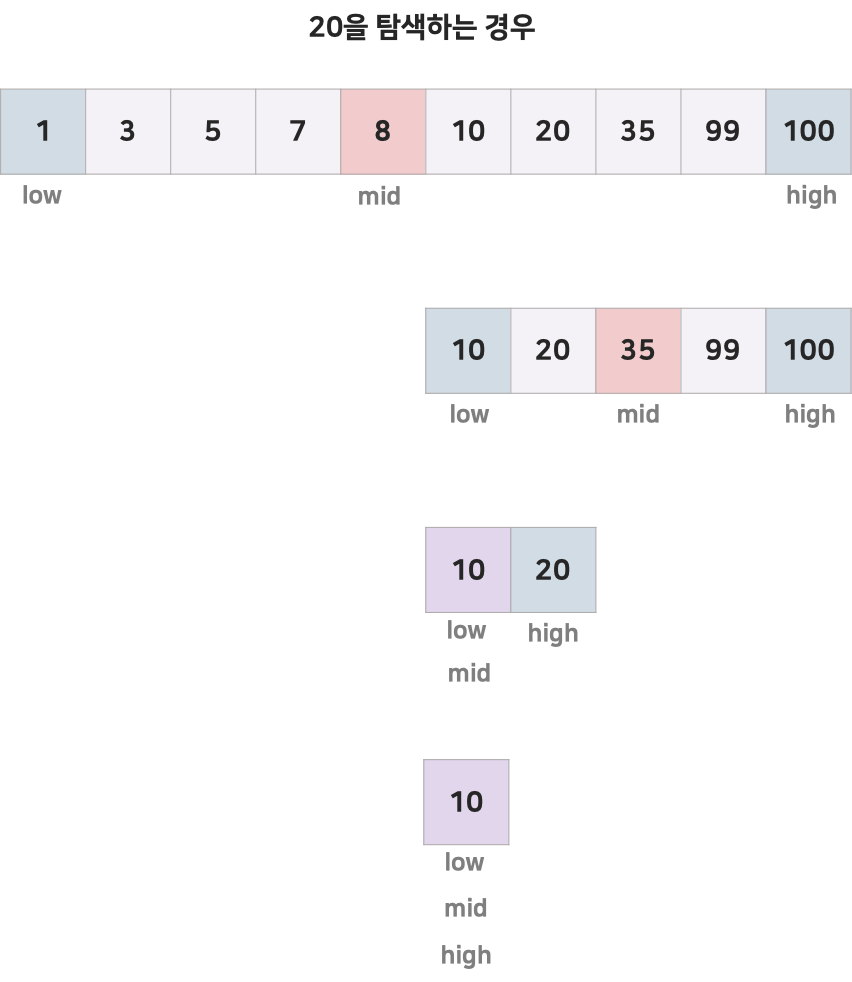
배열의 중간에 있는 값을 조사하여 찾고자 하는 항목이 왼쪽에 있는지 오른쪽에 있는지를 알아내여 탐색의 범위를 반으로 줄인다.
-
찾고자 하는 값이 존재하지 않는 부분은 고려할 필요가 없으므로, 매 단계에서 검사해야 할 배열의 크기를 반으로 줄일 수 있다.
-
데이터의 삽입이나 삭제가 없는 고정된 데이터에 대한 탐색에 적합하다.
시간 복잡도
순차적 탐색 - O(n)
이분 탐색 - O(log n)
이분 탐색 구현 (Java)
재귀 호출을 사용한 이분 탐색 구현
private <T extends Comparable<T>> int binarySearch(
T[] array, // 탐색할 배열
T key, // 찾아야 하는 값
int left, // 탐색할 배열의 시작 인덱스
int right // 탐색할 배열의 마지막 인덱스
) {
if (right < left) {
return -1; // key를 찾을 수 없는 경우 -1을 리턴
}
// 중간값을 찾음
int median = (left + right) >>> 1;
int comp = key.compareTo(array[median]);
// array[median]이 key의 값과 같은 경우
if (comp == 0) {
return median;
}
// array[median]이 key의 값보다 큰 경우
else if (comp < 0) {
return search(array, key, left, median - 1);
}
// array[median]이 key의 값보다 작은 경우
else {
return search(array, key, median + 1, right);
}
}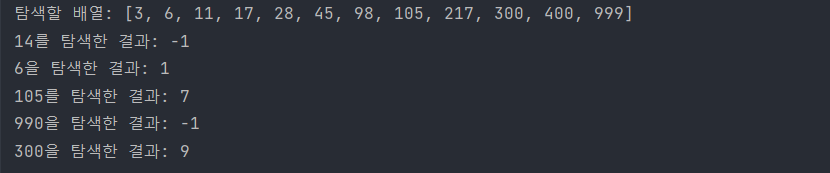
반복을 사용한 이분 탐색 구현
private int binarySearch(int[] array, int target, int left, int right) {
while(left <= right) {
int mid = (left + right) / 2;
if(array[mid] == target) {
return 1;
}
if(array[mid] < target) {
left = mid + 1;
}
if(array[mid] > target) {
right = mid - 1;
}
}
return -1; // 탐색 실패시 -1을 리턴
}