Lecture 4: Optimization - sgd, momentum

강의 영상 주소 : https://www.youtube.com/watch?v=YnQJTfbwBM8&list=PL5-TkQAfAZFbzxjBHtzdVCWE0Zbhomg7r&index=6

해당 슬라이드:
https://web.eecs.umich.edu/~justincj/slides/eecs498/498_FA2019_lecture04.pdf

✍️ [p39 ~p57] 내용 요약정리

<SGD(Stochastic Gradient Descent)>

• 모든 데이터에 대해서 gradient와 loss를 구하기보다는 mini-batch라는 subsample을 만들어서 대략적으로 계산합니다. 보통 이런 subsample의 크기는 대개 2의 제곱수로 32, 64, 128등으로 사용합니다.
• mini-batch를 사용하기 때문에 batch gradient descent보다 계산 속도가 훨신 빠르고 같은 시간에 더 많은 step을 나아갈 수 있습니다.

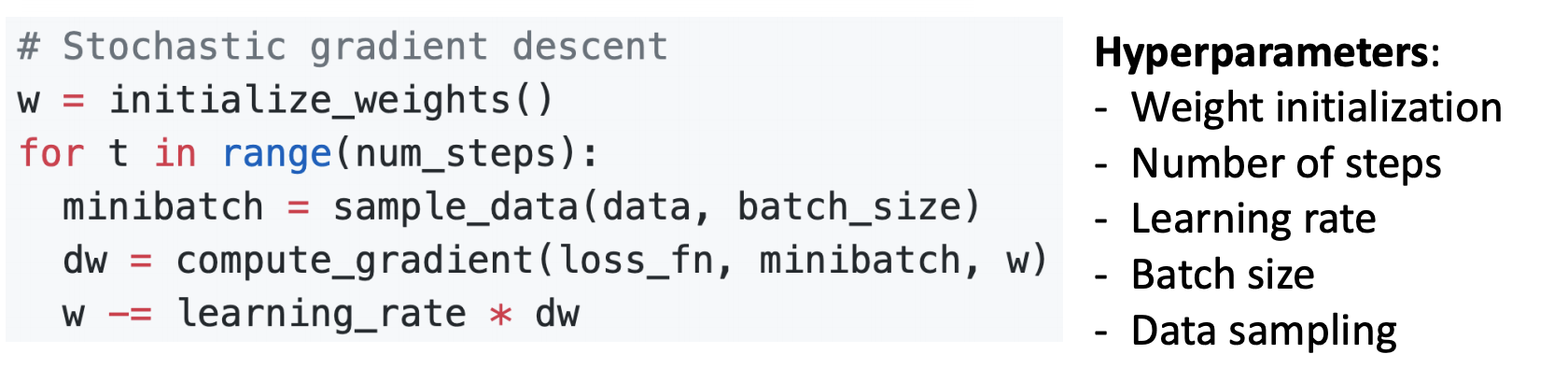
• SGD도 Hyperparameter가 필요한데 SGD에서 Hyperparameter는 기존의 Gradient Descent에서 사용하는 것에 추가로 minibatch 크기인 batch size와 데이터를 어떻게 선정을 할 것인지에 관한 Data sampling이 있습니다.

• 그리고 batch size의 경우 컴퓨터의 GPU의 메모리 크기가 허용하는 한, 최대한 크게 잡는 것이 좋습니다.

• 코드는 gradient descent코드에서 추가로 매 스텝마다 full training data set를 batch size만큼 sampling해주어 mini-batch의 gradient를 구하고 w를 update해줍니다.

• SGD에서는 loss function으로 확률론적으로 접근하기 때문에 stochastic이라는 이름이 덛붙여졌고,

• SGD에서는 표본 데이터를 가지고 gradient와 loss를 구하기때문에 표본 데이터의 분포가 전체 데이터의 분포와 최대한 유사하게 표본을 선정해야 합니다.

<Problems with SGD >

SGD algorithm에는 몇가지 문제가 발생 할 수 있습니다.

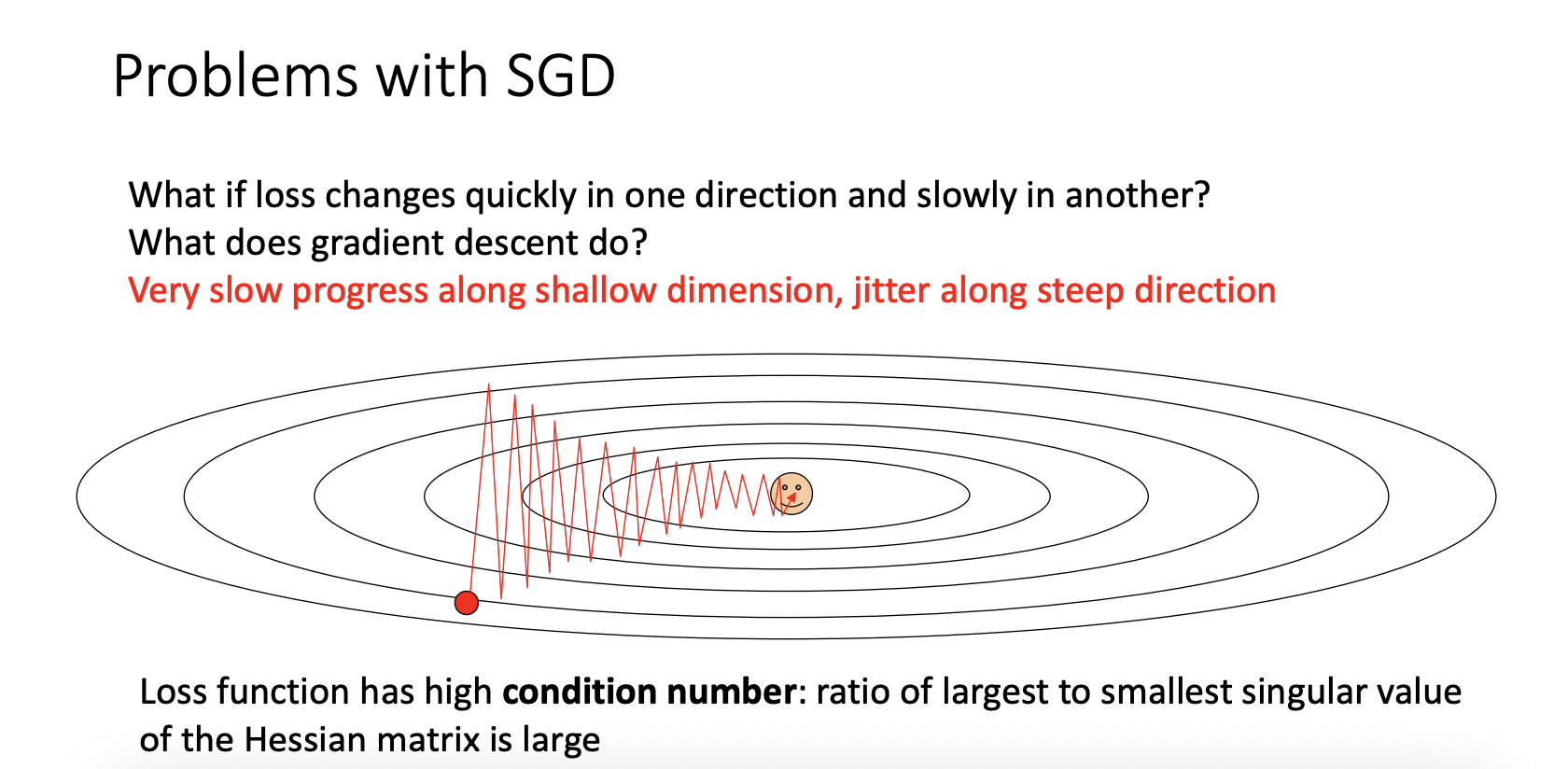
• 첫 번째로는 gradient descent가 지그재그를 그리면서 진행되어 더 많은 step이 소요된다는 점 입니다.

• 이 때문에 SGD는 Full batch보다 Overshooting문제에도 더 취약합니다.

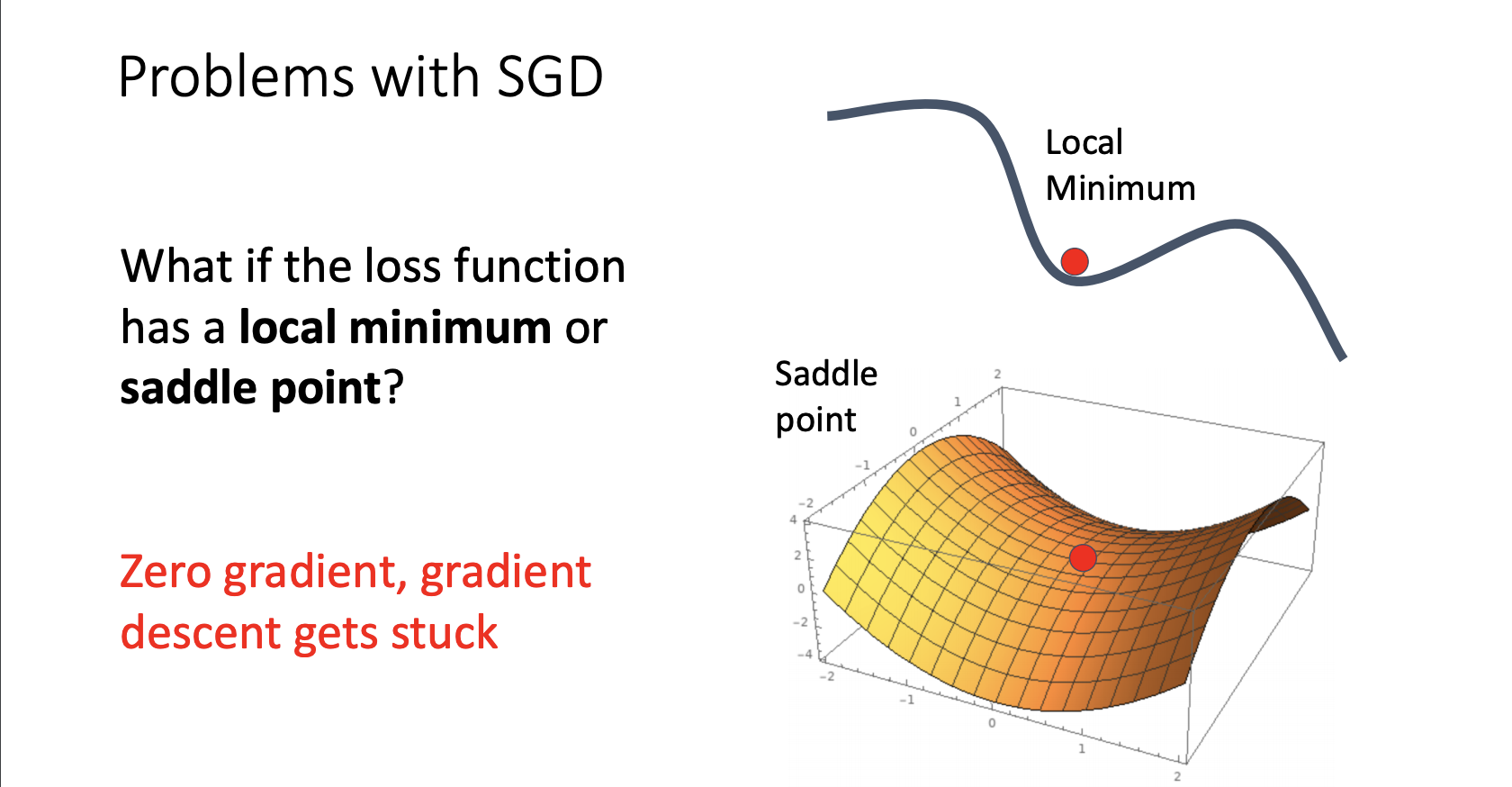
• 두번 째로는 local minimum에 빠질 위험이 높고 saddle point의 경우 gradient가 0으로써 update가 이루지지 않게 됩니다.
  saddle point의 가장 큰 문제점은 saddle point 주변의 기울기는 0이 아니지만 거의 0에 가까운 gradient를 가지고 있기 때문에 update가 상당히 느리게 진행됩니다.
  saddle point의 문제는 고차원에서 상당히 자주 일어나며 거의 모든 고차원 문제에서 겪게 됩니다.

---

[local minimum 문제]

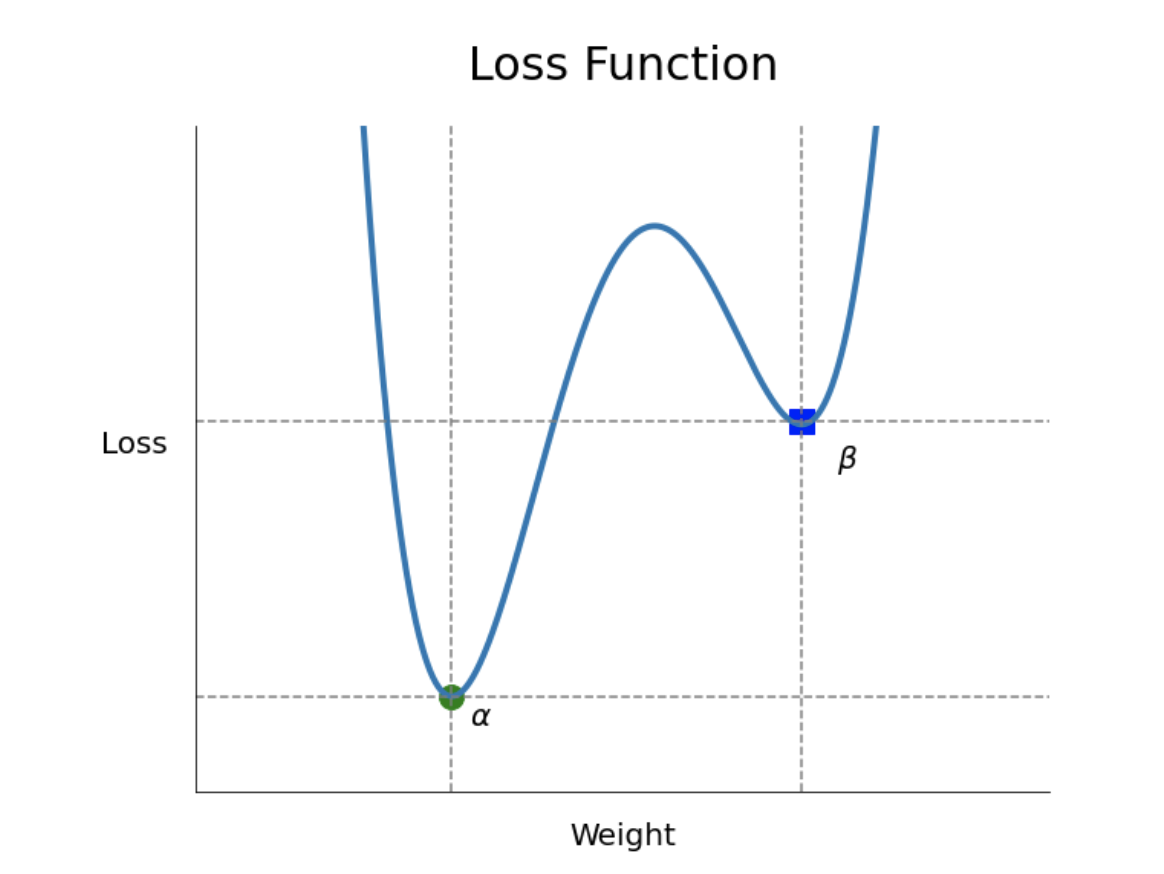
• 그림에서 보이듯이 학습을 진행할 때, 랜덤하게 선택된 가중치가 local minimum에 가까이 있고, local minimum(파란색네모)에 수렴하게되면 실제 목표인 global minimum(초록색점)을 찾지 못하고 학습을 중단하는 문제가 발생할 수 있습니다.

---

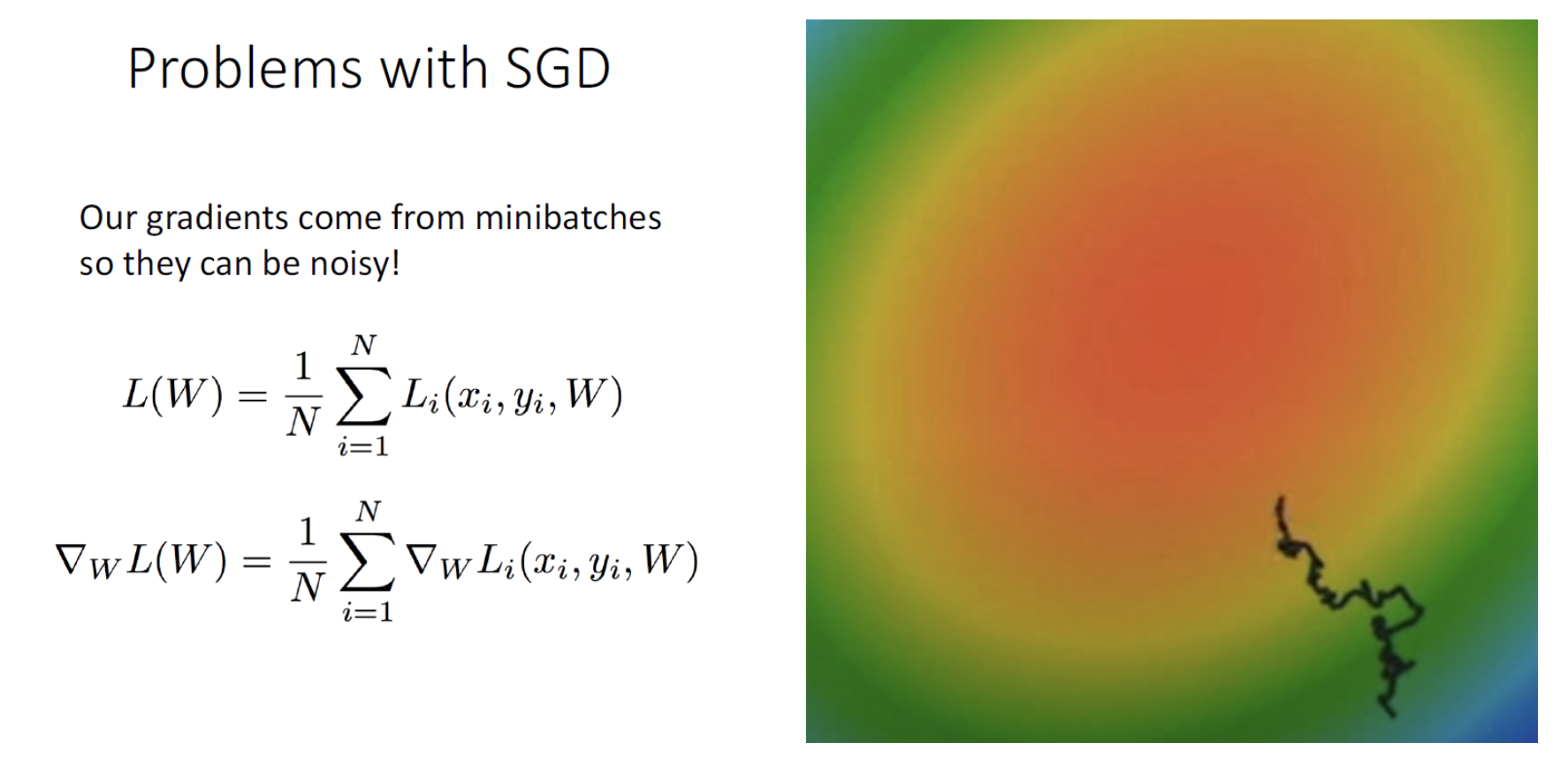
• SGD는 애초에 일부 데이터로만 학습을 진행하기 때문에 Loss Function에서의 W의 궤적이 항상 Loss의 기울기를 따르는 것이 아니라 거꾸로 돌아가기도 하는 등의 노이즈가 생기는 경우가 많습니다.

<SGD + Momentum >

• 위와 같은 SGD문제점때문에 SGD를 약간 변형시켜서 사용하는데 대표적인 방법들 중 하나가 SGD + Momentum입니다.
• 이 SGD + Momentum은 경사하강법에 관성을 더해준건데 이렇게 하면 마치 언덕에서 공이 내려올 때 중간에 작은 웅덩이에 빠지더라도 관성의 힘으로 넘어설 수 있는 효과를 줄 수 있습니다.

• Momentum의 핵심 idea는 weight를 업데이트 할 때 이 전에 계산한 gradient도 반영을 해주자는 건데
  이전의 SGD를 살펴보면 SGD에서는 매 iteration마다 mini-batch sample에서 계산된 gradient를 통해서 weight를 업데이트시키는 방식이었습니다.
• 이전의 gradient도 계속 더해주기 때문에 속력이 아니라 속도(velocity)로 표현
• p는 friction이라고 하며 이전 gradient를 얼마나 고려할 것인지를 뜻하고, 코드에서 rho값은 일반적으로 0.9, 0.99와 같은 값을 사용합니다.
• 즉, 해당 Point에서 마찰계수(friction)를 반영한 속도(velocity)를 먼저 계산하고, 이를 weight update에 사용하는 것입니다.
  이러한 설정으로 경사 낮은 지점에서는 변하는 속도가 느리게, 경사가 가파른 지점에서는 변하는 속도가 빠르게 만들어 줄 수 있습니다.

---

[용어정리]

* Iteration

• 전체 데이터 수와 mini-batch size에 따라 자동으로 결정됨
• = 1 epoch안에서 update가 이루어지는 횟수
• = mini-batch의 개수 (그 안에 있는 데이터의 개수가 아니라 mini-batch자체의 개수)

---

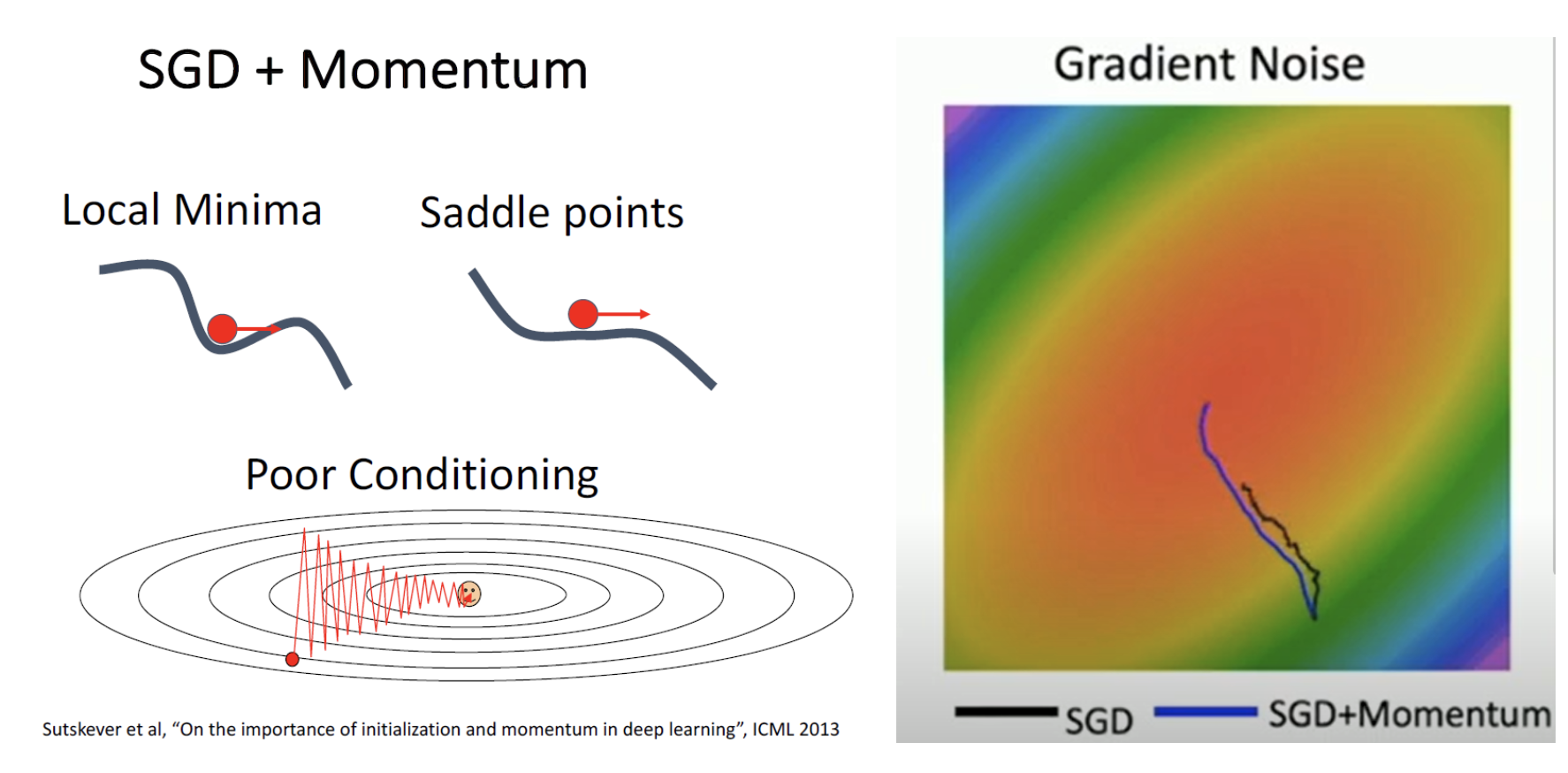
• SGD에서 W가 local Minimum이나 saddle point를 만나더라도 '관성'의 영향을 받아 쉽게 탈출 할 수 있으며
  지그재그로 움직이게 되는 poor conditioning도 완화해줍니다.

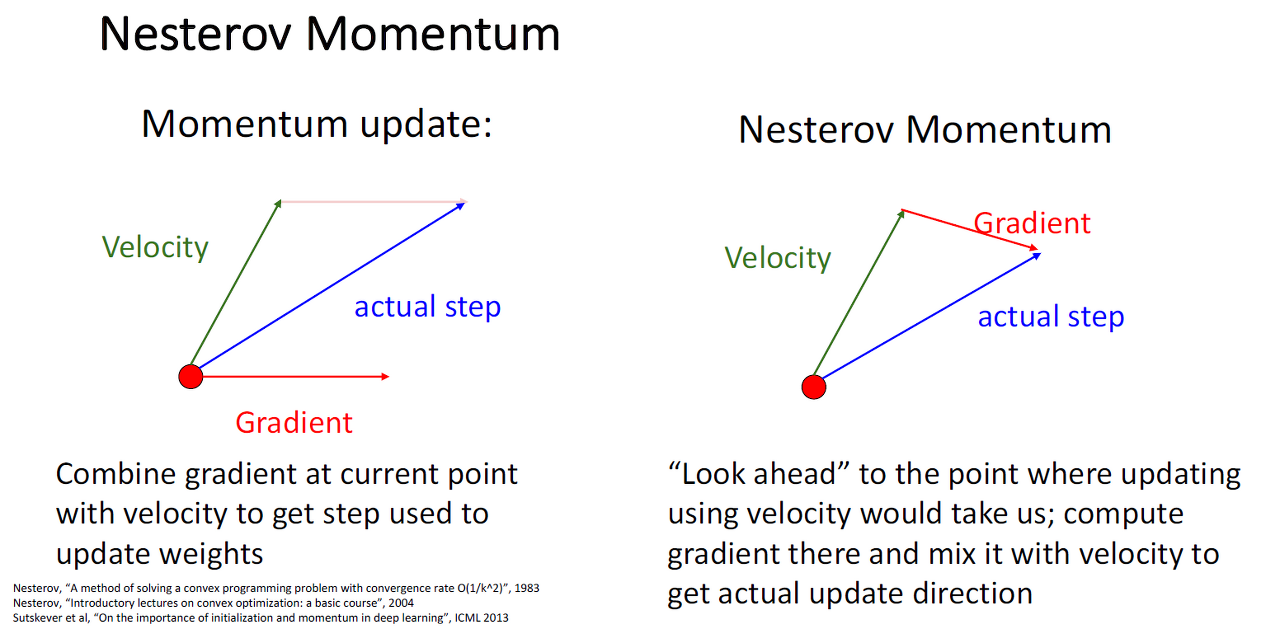
이전의 momentum update
1. 현재 위치에서 gradient를 구한다.
2. 이전 velocity를 가져온다.
3. 이 두가지 방향을 더한 방향으로 한 step간다.

• 현재 지점까지 그동안 누적되어온 속도와 gradient값이 더해져서 실제 step을 이루는 방식
  
  

Nesterov Momentum
1. 이전 velocity를 가져온다.
2. 이전 velocity 방향대로만 갔을 때의 지점에서 gradient를 구한다.
3. 이 두가지를 더한 방향으로 한 step간다.

• momentum값이 적용된 지점에서 gradient값이 계산되는 방식

• Momentum은 현재 update과정에서의 기울기 값을 기반으로 미래값을 도출하도록 되어있습니다. 따라서, 최적의 parameter를 관성에 의해 지나칠 수 있게 된다.
  Nesterov Momentum에서는 Momentum으로 이동된 지점에서의 기울기를 활용하여 update를 수행하기 때문에 이러한 문제를 해소할 수 있게 됩니다.

• 위와 같은 방식으로 Nesterov Momentum을 구하는데 이 방식으로는 api등을 이용하기 쉽지 않아서 아래처럼 살짝 변형해서 적용합니다.

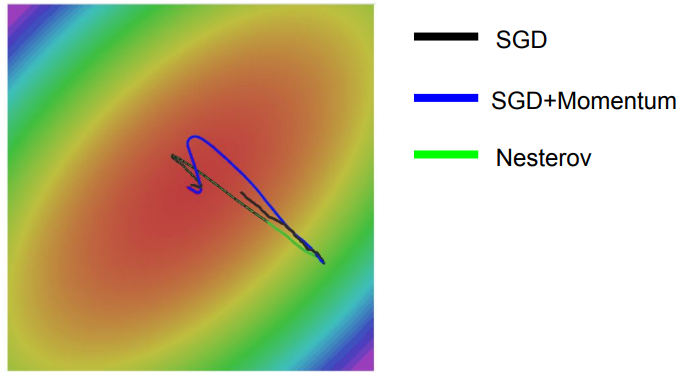
• Nesterov가 SGD, SGD+Momentum보다 훨씬 빠르게 수렴하고 있지만, Nesterov 또한 momentum을 반영했기때문에 overshooting이 여전히 발생하고 있는 것을 확인할 수 있습니다.