Lecture 7 : Convolutional Networks

강의 영상 주소 : https://www.youtube.com/watch?v=ANyxBVxmdZ0&list=PL5-TkQAfAZFbzxjBHtzdVCWE0Zbhomg7r&index=8
해당 슬라이드: https://web.eecs.umich.edu/~justincj/slides/eecs498/498_FA2019_lecture07.pdf

✍️ [p.7 ~ p.38] 내용 요약정리

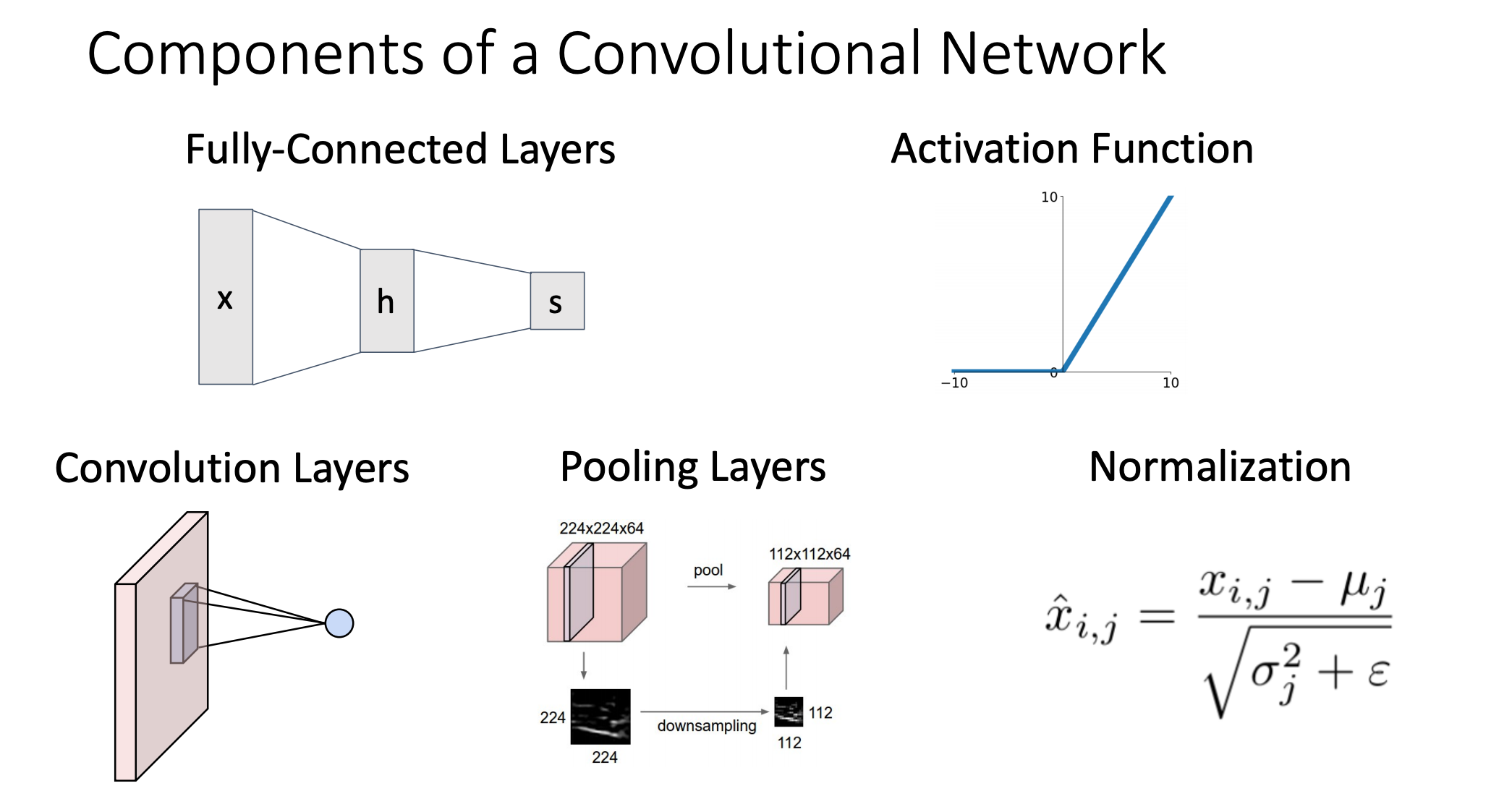
• Convolutional Network에는 3가지 연산들이 있는데 각각 Convolution Layers, Pooling Layers, Normalization이 있다.

• Fully-Connected Layer는 예를 들어 32x32x3 이미지를 3072x1으로 펴서 사용하는 것처럼 입력받은 다차원의 이미지를 하나의 벡터로 만들어서 사용을 함

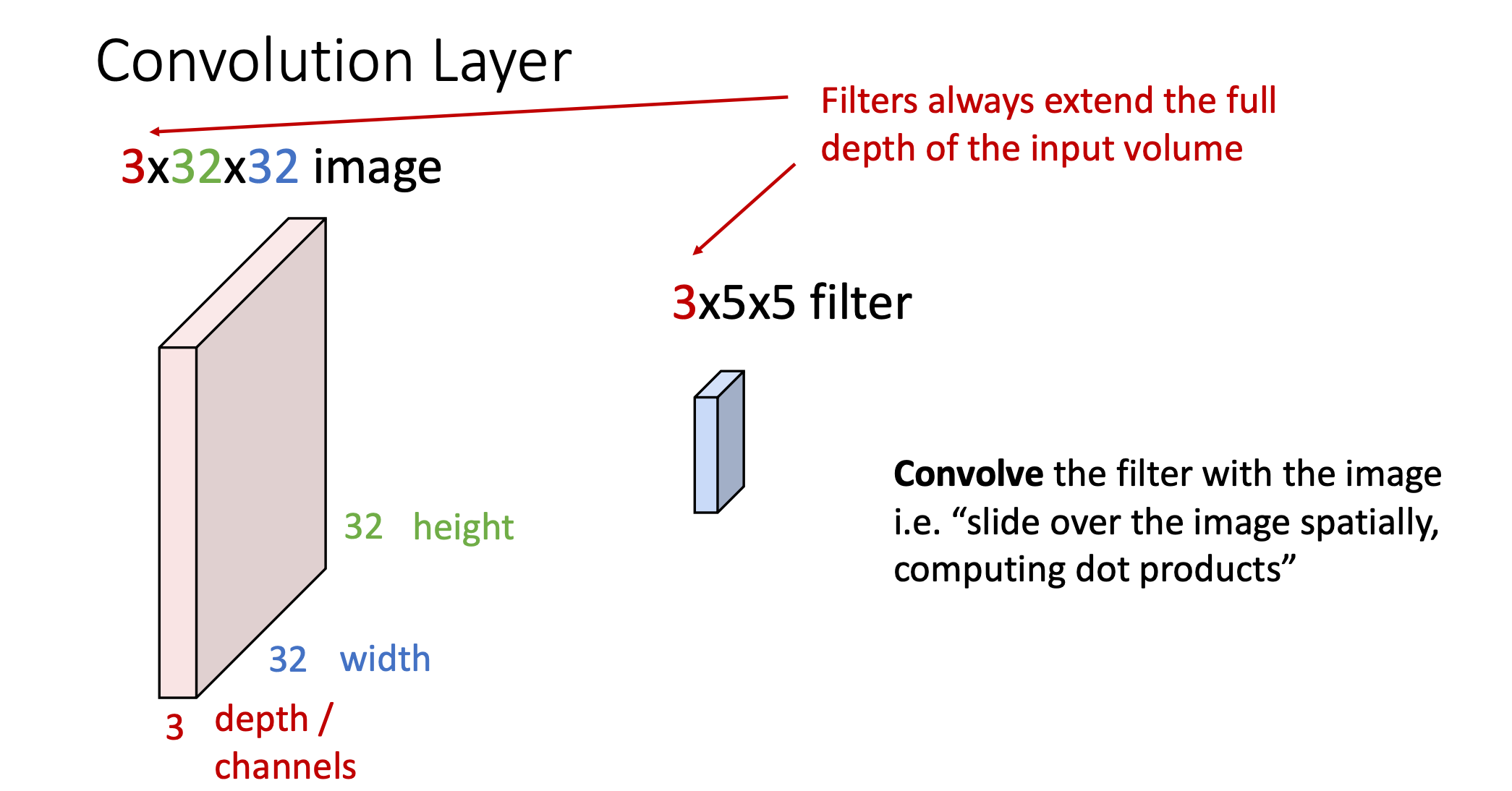
• Convolution Layer는 다차원의 이미지를 하나의 벡터로 늘려서 사용하는 Fully-Connected Layer와는 다르게 기존의 이미지 구조를 그대로 유지함

• 그리고 파란색 필터(3x5x5)는 위에 Fully-connected Layer에서의 가중치역할을 하게되고, 이 필터를 가지고 이미지를 slide하면서 공간적으로 내적을 수행함

• convolution은 이미지 좌 상단부터 시작하고 필터와 접해있는 matrix영역과의 내적을 통해서 값을 리턴하게 됨
• 얻게된 값이 해당 activation map 생성하게 됨
• 입력 이미지와 activation map의 차원이 다른 것을 볼 수 있음(입력: 32x32, activation map: 28x28)
• 32x32이미지를 activation 관점에서 다시 표현된 것이 28x28 결과값이라고 볼 수 있음

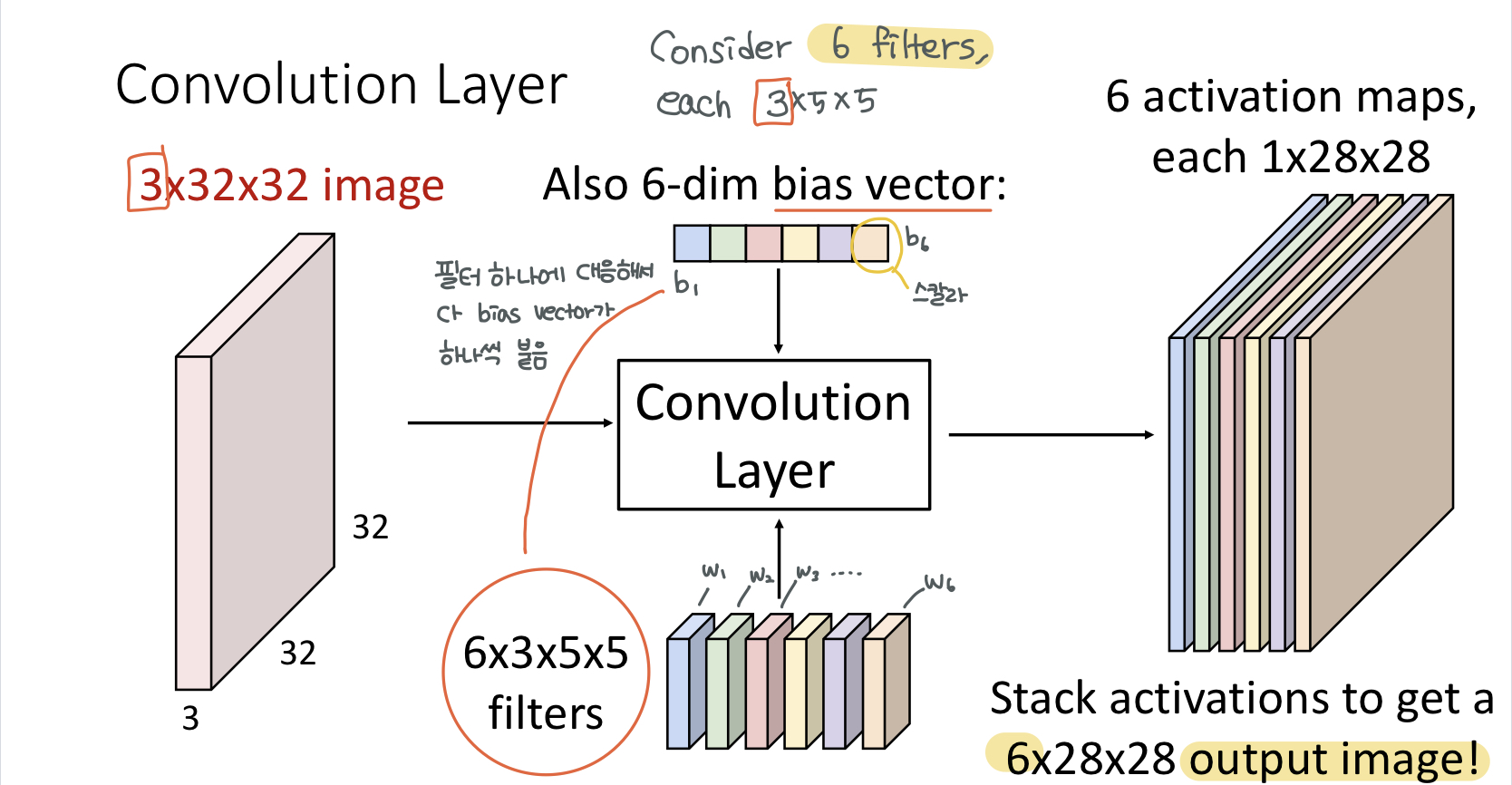
• ouput 이미지를 해석하는 방식이 2가지가 있는데 첫 번째로는 ouput이 지금 6x28x28인데 6개의 activation map이 있다고 해석할 수 있고, 각각 activation map의 갯수는 convolution 필터 갯수와 대응하고 28x28은 이미지가 필터하나에 어떻게 대응하는지에 대한 것에 해당

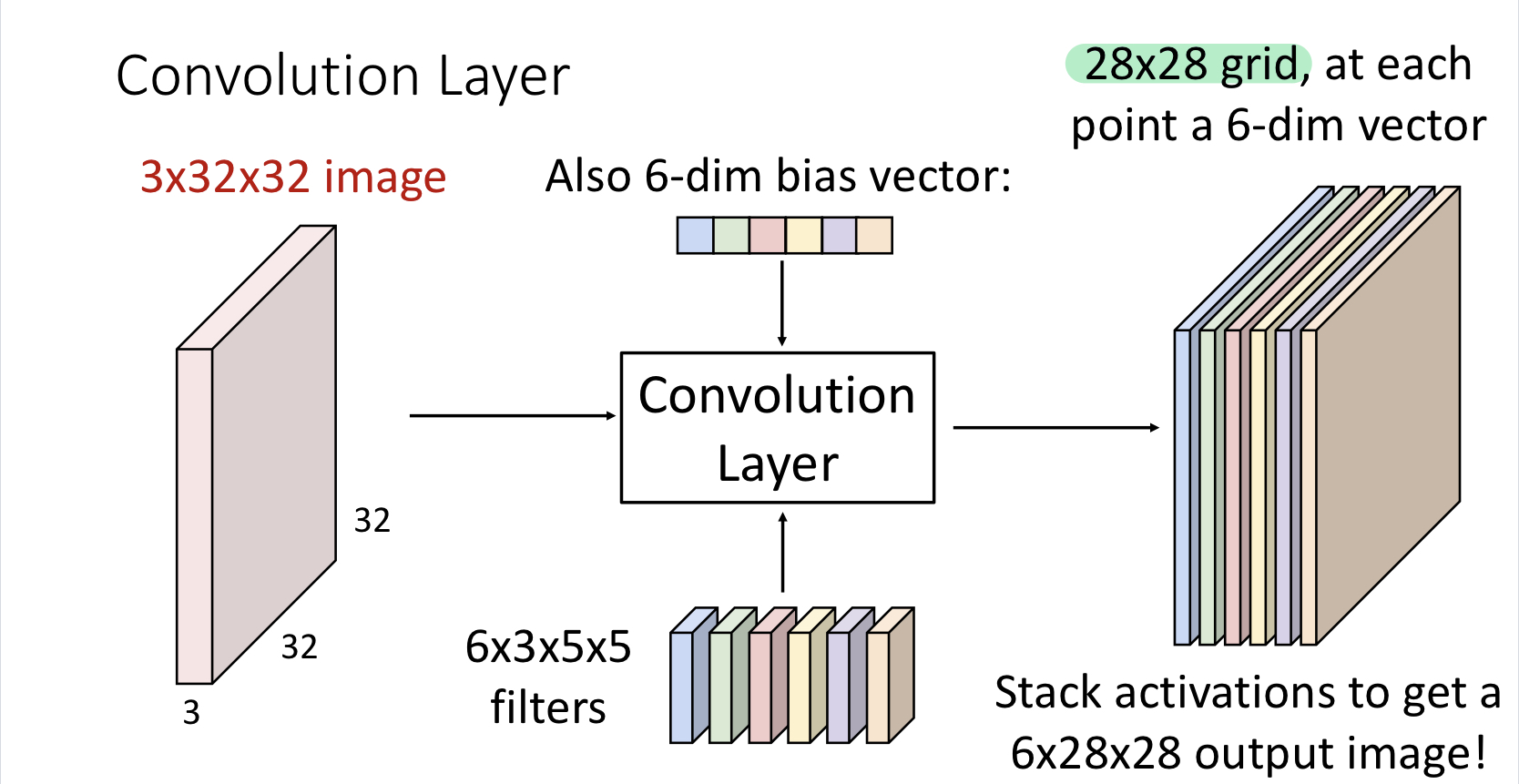
• 두번 째 방식은 output이 28x28 그리드 라고 해석하는 방식인데, 각 그리드가 6-dim vector라고 해석
  이건 어떤 관점에서의 해석이냐면 앞의 5x5영역에서 추출된 피쳐가 6-dim이라고 해석

• 이런식으로 해서 필터가 input 이미지 전체를 slide하게 되면 필터와의 연산 결과로 만들어진 하나의 matrix가 나오는데 이것을 activation map이라고 하고 각 layer에서 여러개의 필터를 사용할 수가 있으며, 여러개의 필터를 사용함에 따라 여러개의 activation map이 나올 수 있음

• 여러개의 필터를 사용하는 이유는 필터마다 다른 특징을 추출해내고 싶기 때문

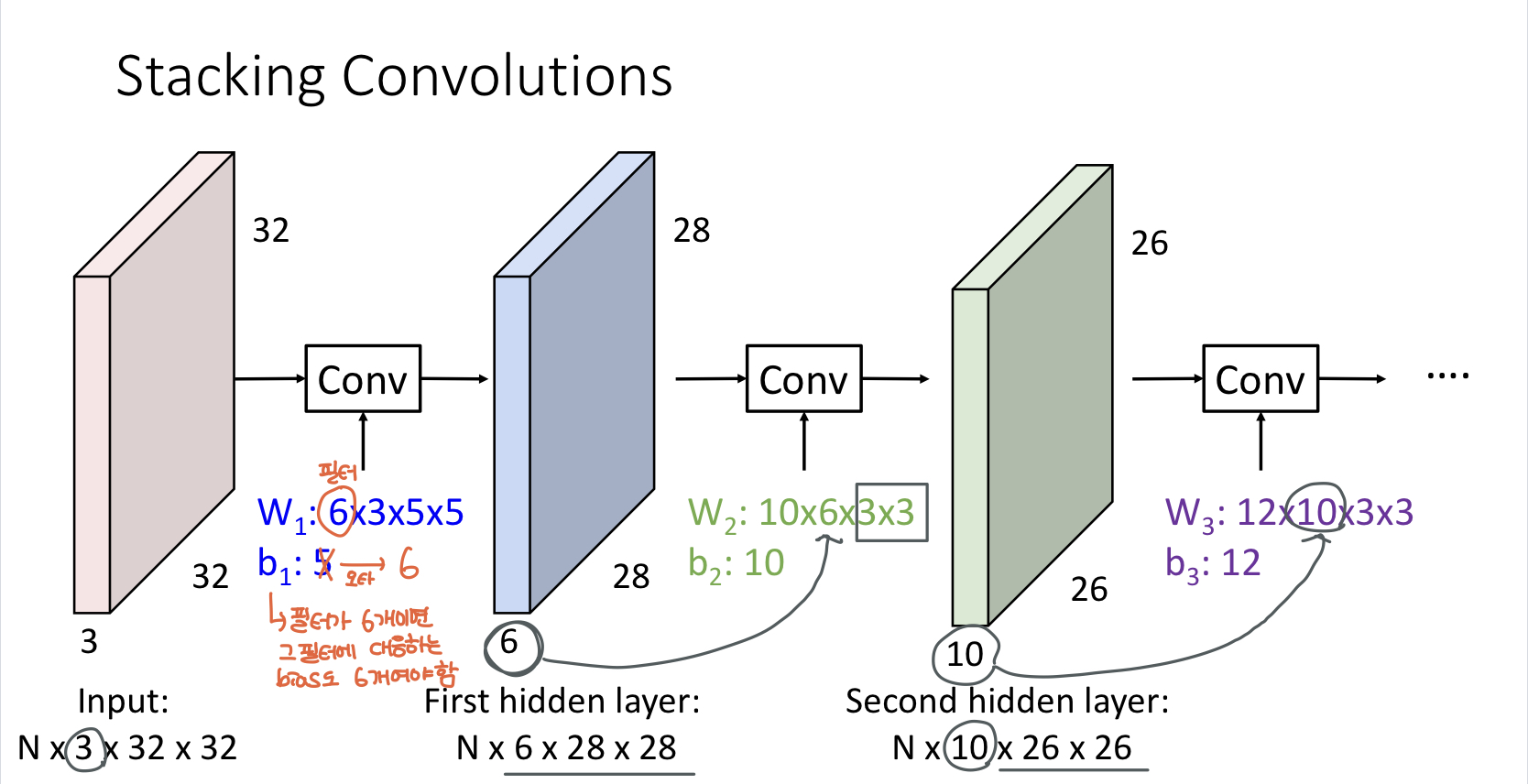
• 처음 input 3x32x32 이미지에 대해서 필터를 6개를 적용함 (필터가 6개면 그 필터에 대응하는 bias도 6개) 적용하게 되면 28x28 activation map이 6개가 나옴

• 6x28x28에 대해서 또 convolution을 하게 되는데 두번째에서는 3x3필터를 사용했고 10x6x3x3에서 6은 두번째 convolution 입장에서 input 채널이 6개여서 그렇고 10은 필터를 10개를 적용하겠다는 내용임

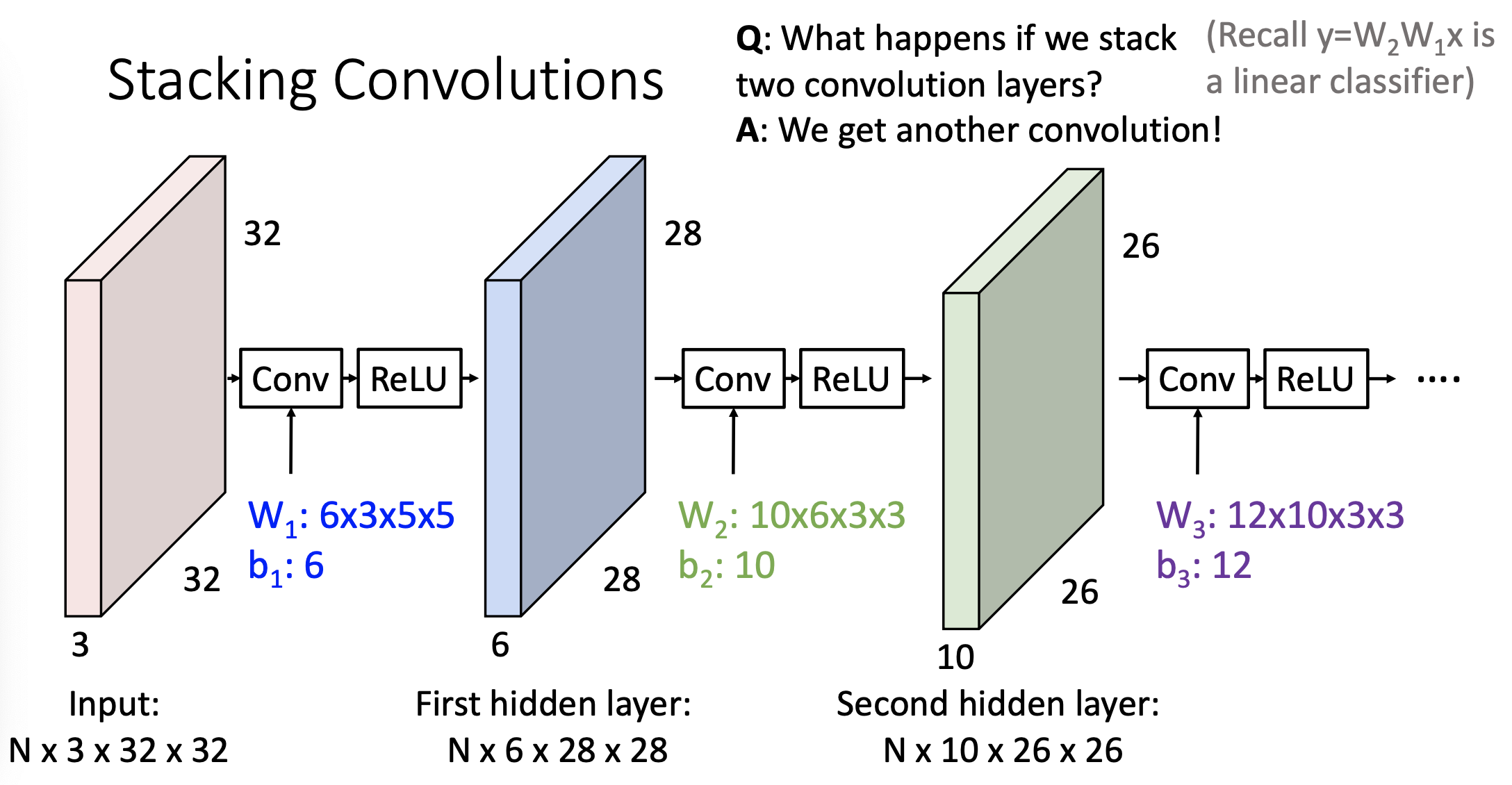
• convolution layer는 Linear 연산을 수행함

• fully-connected layer에서 lineaer transform하고 ReLu함수를 적용한것 처럼
  여기에서도 convolution layer를 하고 나서 ReLu activation 함수를 적용해줌

• 전체적인 변환들이 non-linear변환이됨

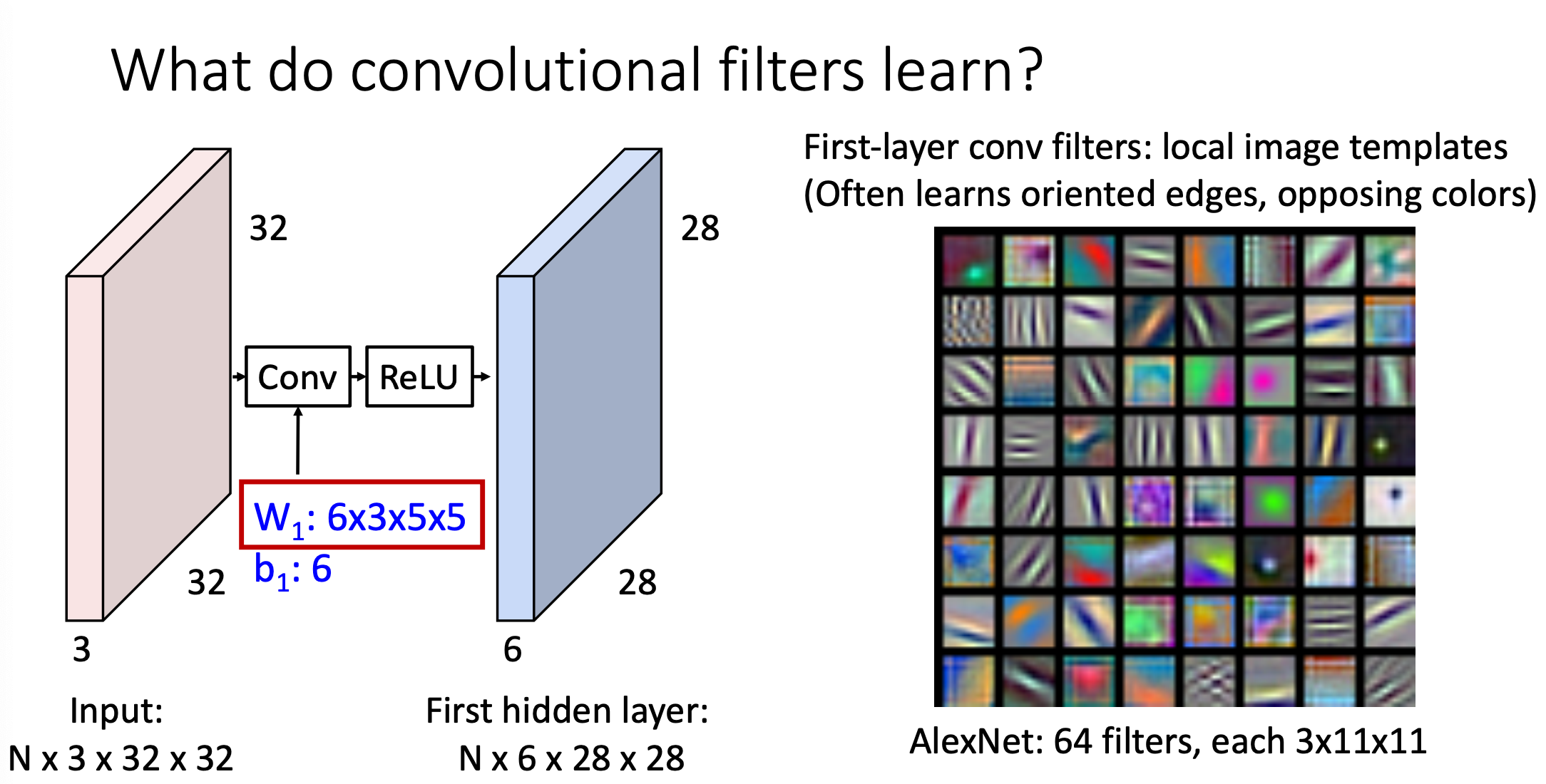
• Convolution Layer의 특징으로는 Full-Connected Layer가 입력과 동일한 이미지의 템플릿을 학습하는 것과 달리, filter가 local template을 학습한다는 점이 있다.
  그리고 output에서의 feature vector의 각 원소는 각 filter(local pattern)와 얼마나 일치하는지를 나타냄

• neural network에서 첫 번째 레이어에 대해서 64개의 필터를 적용하고 시각화 한 그림이다.
  우리는 각 이미지에 대해서 필터 하나하나를 내적을 취해서 feature를 뽑아내는데 내적을 취하는 이 필터가 어떻게 생겼냐면 위에 그림처럼 edge에 뭔가 하이라이트를 한 것 같은 모양으로 생겼음

• AlexNet의 First-layer convolutional filter는 기울어진 edge들을 다 빼내는 추출기의 역할을 하겠구나라고 생각할 수 있고, 저 색깔들이 실제 이미지의 보색으로 되어있다고 함 그래서 색깔같은 경우에도 보색으로 추출하는 구나라고 생각할 수 있음

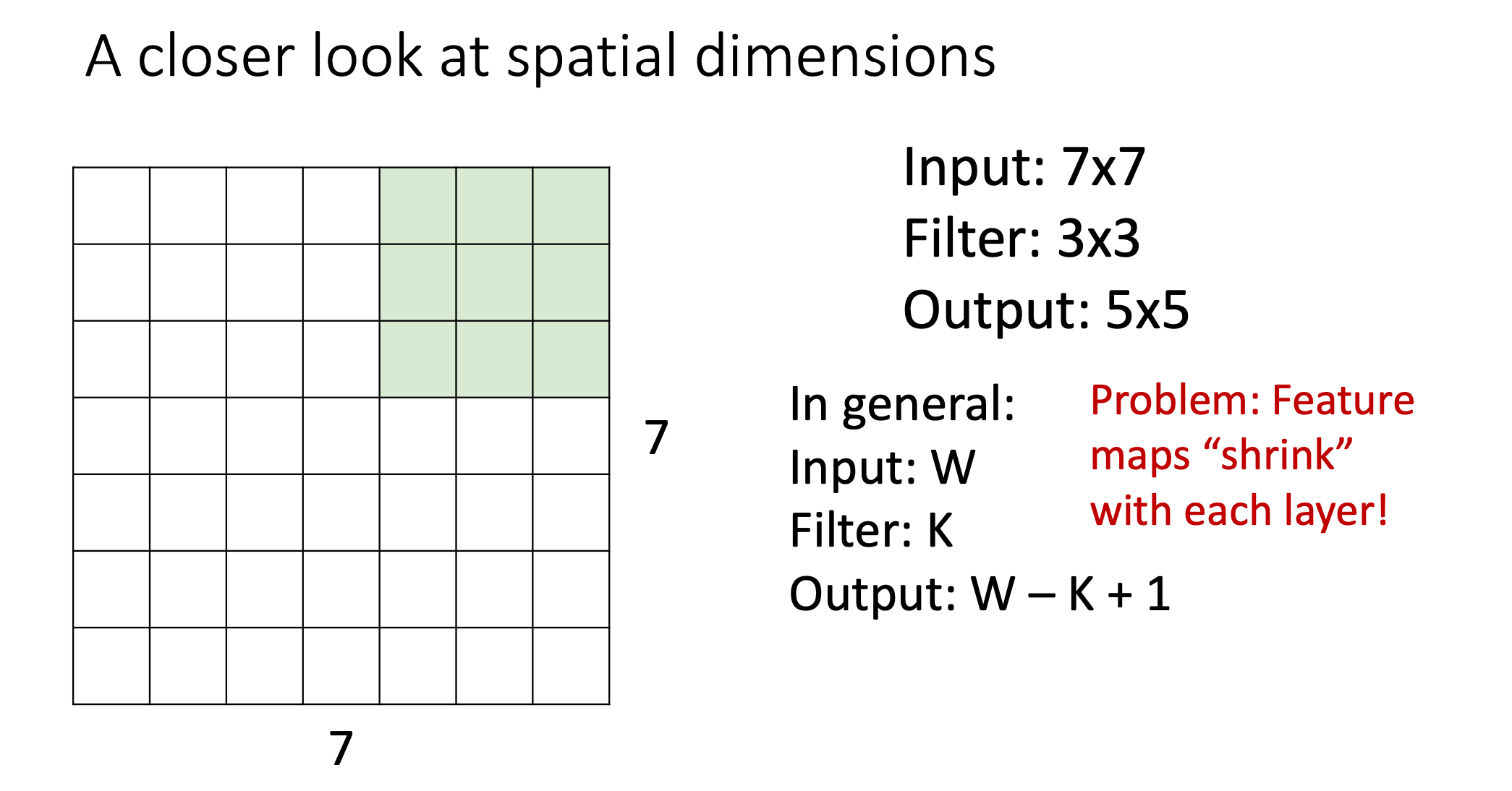
• 여기서는 stride를 1로 해서 1씩 필터를 slide해가면서 output이 5x5로 나오는 것을 알 수 있음

• 이렇게 layer를 거치게 되면 volume 자체가 점점 줄어드는 것 즉, shrink하는 것을 볼 수 있음
• 수 만개의 layer를 거친다면 처음 input보다 점점 shrink해버려서 더 이상 convolution을 진행할 수 가 없게 되기 때문에 이런문제를 해결하기 위해서 padding을 사용함

• padding은 feature map 가장자리에 임의의 픽셀을 추가해주는 것을 말하는데, 주위 픽셀의 평균으로 추가하거나, 근처의 값의 복사하는 등 여러 가지 방법이 있지만 대부분의 경우, 그냥 0을 추가하는 'Zero Padding'이란 것을 많이사용함

• 그리고 얼마나 Padding 할지는 Hyperparameter P에 따라 정해지는데 P가 정해지면 Input의 크기와 Filter의 크기가 각각 W, K라고 할 때 Output의 크기는 W - K + 1 + 2P가 된다.

• padding을 하는 가장 큰 이유는 input의 크기가 shrink하지 않게 하기 위해 사용하게 되고 즉, output 크기가 input크기와 같게 하기 위해 사용함