서론

[PLM을 이용한 혐오 표현 탐지 모델] 프로젝트를 진행하던 중, 모델 성능 향상을 위한 방법 중 하나로 unlabeled data를 활용하기를 생각했다. 지금까지 진행했던 연구에서는 항상 레이블이 있는 데이터를 대상으로 supervised learning만을 했기 때문에 unlabeled data를 활용하는 방법에 대한 지식이 부족했다. 이에 따라 labeled+unlabeled를 사용하기 위해 semi-supervised learning에 대해서 간단하게 알아보고, NLP에서의 semi-supervised learning 방법론에 대해 리서치를 진행해봤다.

Background

MixMatch: A Holistic Approach to Semi-Supervised Learning

🖇️ Reference
https://arxiv.org/abs/1905.02249
https://www.youtube.com/watch?v=nSJP7bn2D1U
https://www.youtube.com/watch?v=-klr7a7jyus
https://www.youtube.com/watch?v=-pdrOYcgSrE

1. Introduction

semi-supervised learning

• supervised loss + unsupervised loss로 total loss(semi-supervised loss)를 계산
• unsupervised loss는 주로 이전에 본 적 없던 데이터에 대해 일반화를 시키기 위해 사용됨
• semi-supervised learning에 관한 논문들에서는 unsupervised loss를 계산하고 최적화 하는 방식에 대한 연구를 진행

recent trends

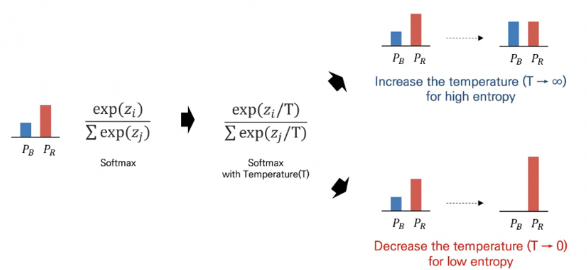
Entropy Minimization : unlabeled 데이터에 대한 예측값의 확실성을 높이기 위한 목적으로 사용

• 학습 방식
  • labeled 데이터를 이용하여 학습을 완료한 supervised model이 필요
  • 학습한 모델을 이용하여 unlabeled data에 대한 인퍼런스 진행
  • 예측값의 확실성을 높이기 위해서 위에서 인퍼런스를 진행한 확률 값을 높이는 방향으로 엔트로피를 최소화함(논문에서는 Softmax Temperature 사용. $T$ 가 temperature의 역할. 0으로 갈수록 엔트로피가 작아짐.)

		엔트로피가 작아지면 확률이 극단적으로 변하고, 엔트로피가 커지면 불확실성이 증가하여 확률 값이 평평해짐

Consistency Regularization

• unlabeled data에 augmentation을 적용하면 예측했을 때의 확률 값 분포가 달라지는데, 이 때 모델이 예측한 전후의 확률 분포가 동일하도록 학습(아래 그림의 왼쪽, 오른쪽 분포)
  
• squared loss term 등을 사용하여 분포의 유사성을 높임

MixUp

• 데이터와 레이블 각각에 convex combination을 적용하여 새로운 데이터를 생성함으로 등장하지 않았던 데이터에 잘 적응하도록 함(오버피팅 방지)

• supervised data에서는 실제 레이블을 사용
  

• unsupervised data에는 모델이 예측한 확률값(가짜 레이블)을 사용
  

2. MixMatch

MixMatch의 과정

(1) Data Augmentation

• labeled data에 stochastic data augmentation 적용
  • 사전에 정의된 augmentation 기법(이미지 대상 - 크롭, 대칭 ,회전, 확대 등) 중 하나를 임의로 적용
  • 이미지를 크롭, 대칭, 회전 등을 적용한다고 해도 대상이 달라지는 것이 아니기 때문에 레이블은 그대로 유지가 됨

• unlabeled data에 stochastic data augmentation k번 적용
  → 배치 내에 B개의 labeled data와 B개의 unlabeled data가 존재한다고 가정한다면, Data Augmentation 단계 이후에는 B개의 labeled data와 B*k개의 unlabeled data가 생성됨

(2) Label Guessing

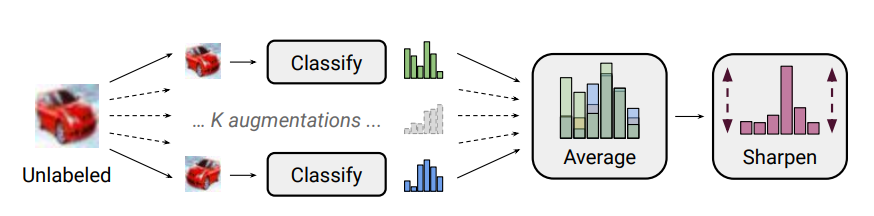
• labeled data를 이용하여 supervised learning을 진행한 모델을 이용하여 새로운 데이터의 레이블을 예측하고 그 평균 값을 구함
  $\bar q_b = {1 \over K } \sum_{k=1}^K \mathrm p_{model}(y|\hat u_{b, k};\theta)$

• 평균 값을 softmax temperature를 이용하여 Entropy Minimization(Sharpening)
  $Sharpen(p, T)_i = {p_i^{1\over T} \over \sum_{j=1}^L p_j^{1 \over T}}$
  → 이 과정을 거쳐서 얻은 값을 guessed label로 사용
  

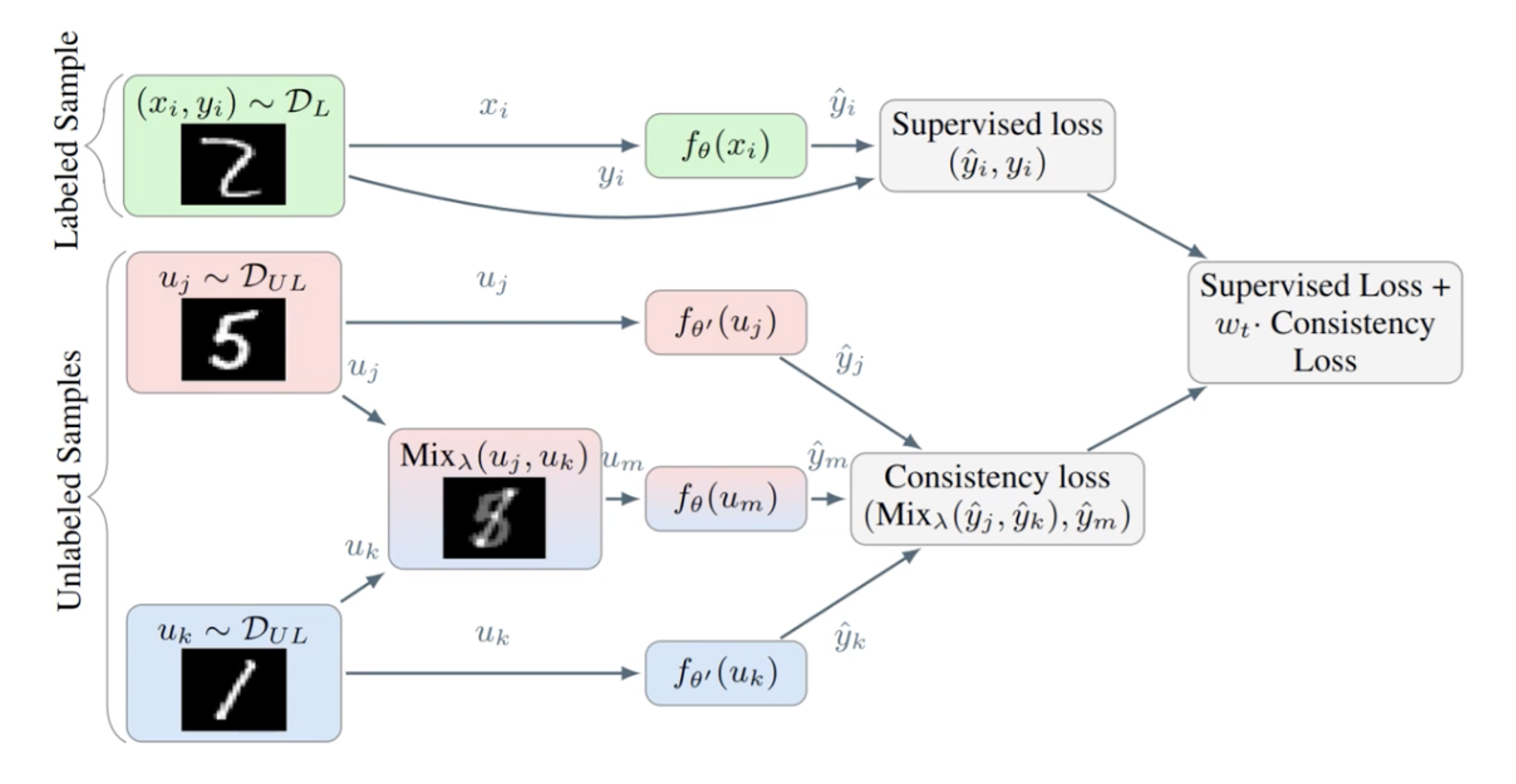
(3) MixUp

• 기존에 semi-supervised에서는 unlabeled 데이터만을 가지고 MixUp을 수행했지만, MixMatch 논문에서는 labeled, unlabeled 데이터 모두 사용하여 MixUp을 수행
  • 기존 방식
    
    $\lambda \sim Beta(\alpha, \alpha) \\ x' = \lambda x_1 + (1-\lambda)x_2 \\ p' = \lambda x_1 + (1-\lambda)p_2$
  • MixMatch에서의 MixUp
    $\lambda \sim Beta(\alpha, alpha) \\ \lambda' = max(\lambda, 1-\lambda) \\ x' = \lambda' x_1 + (1-\lambda')x_2 \\ p' = \lambda' p_1 + (1-\lambda')p_2 \\$

• MixMatch에서는 labeled 데이터는 labeled 데이터끼리, unlabeled 데이터는 unlabeled 데이터끼리 MixUp을 적용하는 것이 아님. 아래와 같이 생성된 데이터를 모두 섞은 후 랜덤으로 선택된 데이터를 이용하여 MixUp을 적용함.
  $\mathcal X' = (MixUp(\hat{\mathcal X}_i, \mathcal W_i); i \in (1, ..., |\hat {\mathcal X}|)) \\ \mathcal U' = (MixUp(\hat{\mathcal U}_i, \mathcal W_{i+|\hat{\mathcal X}|}); i \in (1, ..., |\hat {\mathcal U}|))$
  • $\mathcal W$ : 생성된 labeled, unlabeled 데이터($\hat{\mathcal X}, \hat{\mathcal U}$)를 합친 후, 섞은 데이터셋

(4) Loss Function

• 위 과정을 통해서 새로운 labeled, unlabeled 데이터들이 생성됨
  $\mathcal X', \mathcal U' = MixMatch(\mathcal X, \mathcal U, T, K, \alpha)$

• 생성된 데이터를 이용하여 *Supervised loss + Consistency loss($\mathcal L = \mathcal L_s + \lambda_u \mathcal L_u$)*를 계산
  $\mathcal L_x = {1 \over |\mathcal X'|} \sum_{x, p \in \mathcal X'} H(p, \mathrm p_{model}(y|x; \theta)) \\ \mathcal L_u = {1 \over L|\mathcal U'|} \sum_{u, q \in \mathcal U'} \rVert q - \mathrm p_{model}(y|u;\theta) \rVert_2^2$
  • labeled 데이터는 cross entropy를 이용하여 supervised loss를 계산
  • unlabeled 데이터는 L2 loss를 이용하여 consistency loss를 계산

---

Text Augmentation

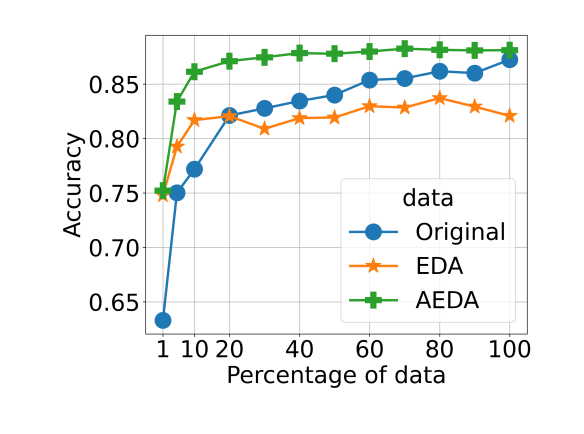
EDA

• Easy Data Augmentation(https://arxiv.org/pdf/1901.11196.pdf)
• 원 문장의 토큰을 유의어 대체, 랜덤 추가, 랜덤 삭제, 랜덤으로 자리 바꾸기 등을 적용하는 방식

AEDA

• An Easier Data Augmentation(https://arxiv.org/pdf/2108.13230.pdf)
• 원문장의 다량의 구두점을 추가하는 방식

Back Translation

• Understanding Back Translation at Scale(https://arxiv.org/abs/1808.09381)
• A언어에서 B언어로 번역한 뒤, 다시 A언어로 번역하여 기존 문장의 의미는 유지되면서 형태가 약간 변하는 것을 통해 데이터 증강하는 방식

---

Semi-supervised Learning on Text Data

UDA

https://arxiv.org/pdf/1904.12848.pdf

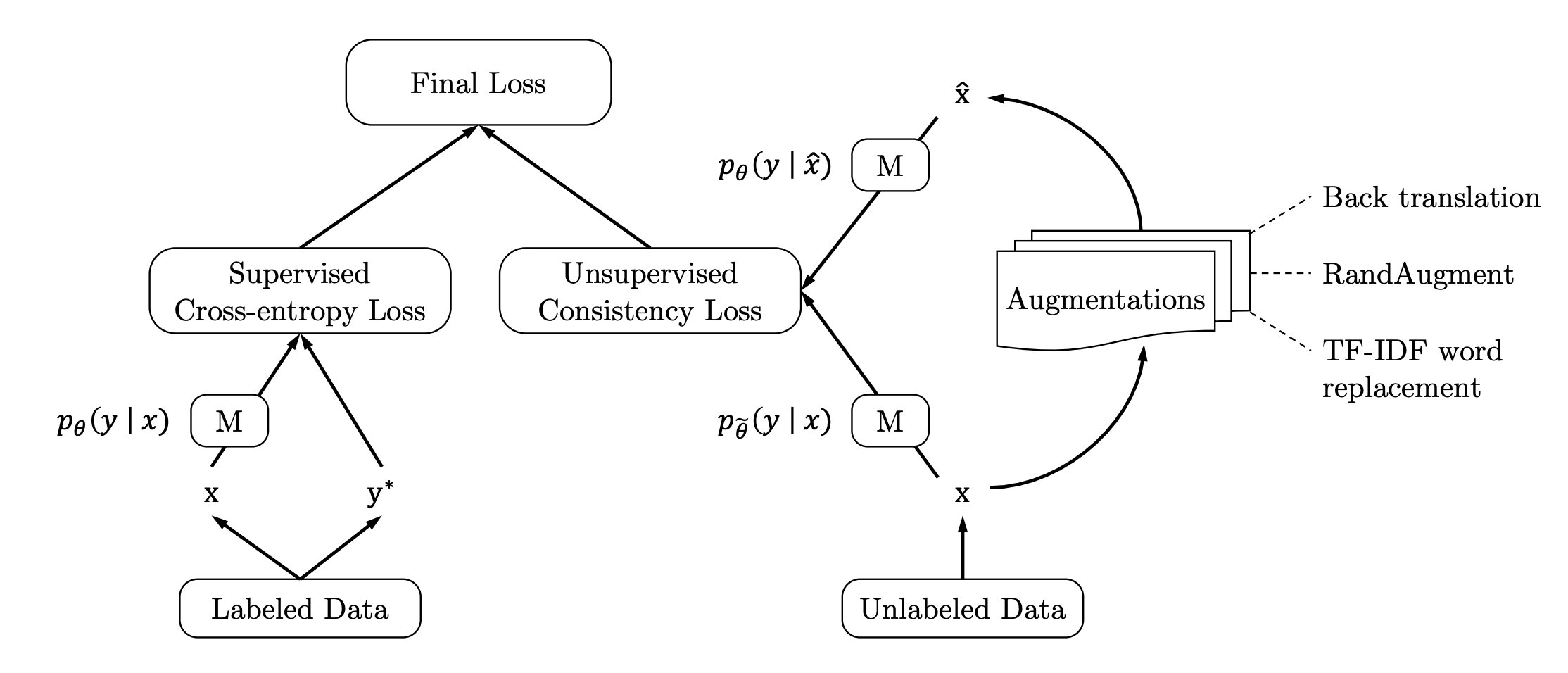
1. 소수의 labeled data와 다수의 unlabeled data를 사용하며, 각각 supervised loss(cross entropy)와 unsupervised loss(consistency)를 사용하는 것은 MixMatch와 동일
2. MixUp을 통해서 새로운 데이터 샘플을 만드는 것 대신에 Back translation을 포함한 자연어에 대한 augmentation 기법을 적용하여 [unlabeled data - augmented data]의 consistency 계산

MixText

🖇️ Reference
https://arxiv.org/pdf/2004.12239.pdf
https://www.youtube.com/watch?v=rcZi8k3Gr9A

MixMatch의 MixUp, Label Guessing + UDA의 Back Translation을 활용한 방식

1. TMix(Text Mixup)

• Mixup은 이미지에 대한 데이터 증강 기법으로 사용되고 있었음. 보통 Mixup 단게에서는 두 개의 이미지를 섞는 과정이 필요한데 텍스트에서는 이 과정을 그대로 적용할 수 없다는 문제가 존재함(discreteness)
  → BERT의 hidden representation에 대하여 가중합을 적용하는 방식으로 두 문장을 섞어보자
  

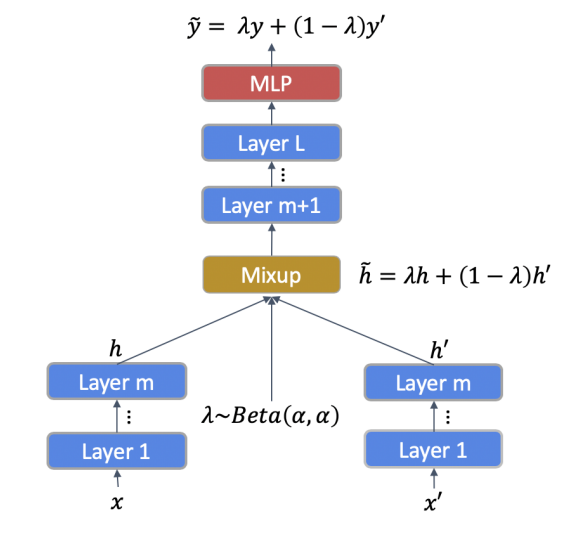
• 두 개의 문장을 각각 BERT의 인풋으로 사용하여 각각에 대한 BERT hidden representation을 얻게 됨
  • BERT의 인코더가 총 $L$개의 레이어로 이루어져 있다면, mixup을 적용할 층 $m$을 선택함; $m \in [1, L]$
    $h_l^i = \mathrm{BERT}_l(h_{l-1}^i;\theta), l \in [1, m], \\ h_l^j = \mathrm{BERT}_l(h_{l-1}^j;\theta), l \in [1, m],$
  • 이 때, $m$번째 레이어까지 구한 hidden representation에 대해 가중합을 적용
    $\tilde h_m = \lambda h_m^i + (1-\lambda)h_m^j, \\ \tilde h_l = \mathrm{BERT}_l(\tilde h_{l-1}; \theta), l \in [m+1, L].$
  • 위 과정을 통해 얻은 가중합 은닉 벡터를 다시 BERT의 $m$번째 레이어의 인풋으로 사용하여 최종 마지막 레이어의 벡터 값($\tilde h_L$)을 TMix의 결과로 사용
    • 두 문장($x, x'$)에 대한 TMix 결과 : $\tilde h_L$
    • 두 레이블($y, y'$)에 대한 TMix 결과 : $y, y'$의 가중합($\tilde y = \lambda y + (1-\lambda )y'$)

• TMix에서 MixUp을 진행할 레이어의 선택 방법은 아래 논문을 참고하여 결정했다고 함.
  • What does BERT learn about the structure of language?
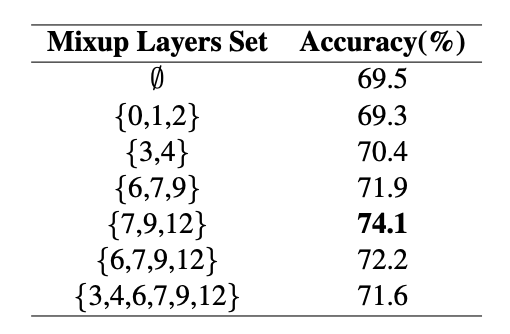
  • representation power가 높은 {3, 4, 5, 6, 7, 9, 12} 중에서 {7, 9, 12}를 후보로 설정
  • {7, 9, 12} 중에서 지속적으로 하나의 층을 랜덤으로 선택하여 Mixup을 적용(TMix 내에서는 한 번의 Mixup이 이루어짐)
    

2. Semi-supervised MixText

TMix를 Data Augmentation으로 활용한 Semi-supervised learning 방법으로 MixMatch의 과정과 거의 동일

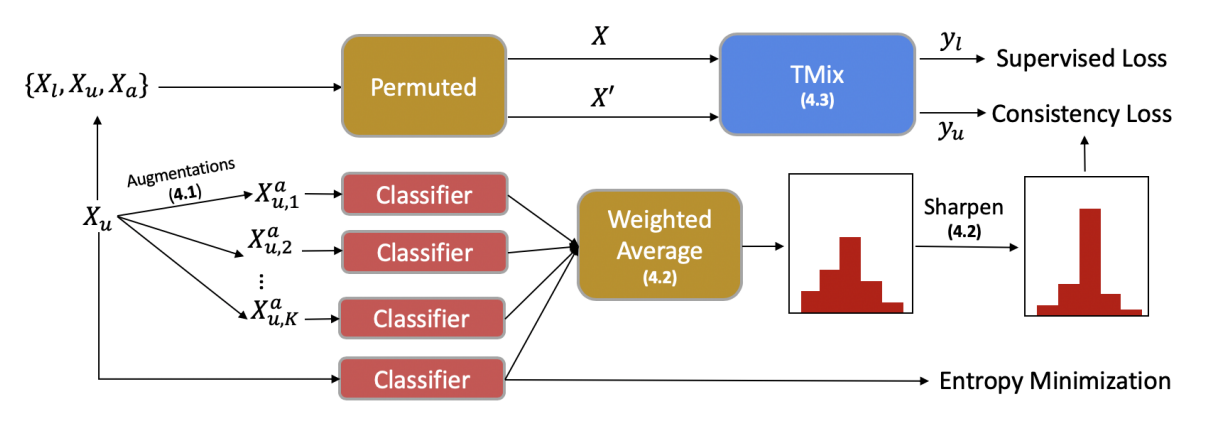
Data Augmentation

• unlabeled data를 증강시키기 위해서 back translation을 적용
• unlabeled text set $X_u$의 각각의 문장 $x_i^u$에 대해 $K$번의 back translation을 적용.
  • 이 때, K번의 역번역은 모두 다른 언어로 역번역을 진행함.
    

Label Guessing

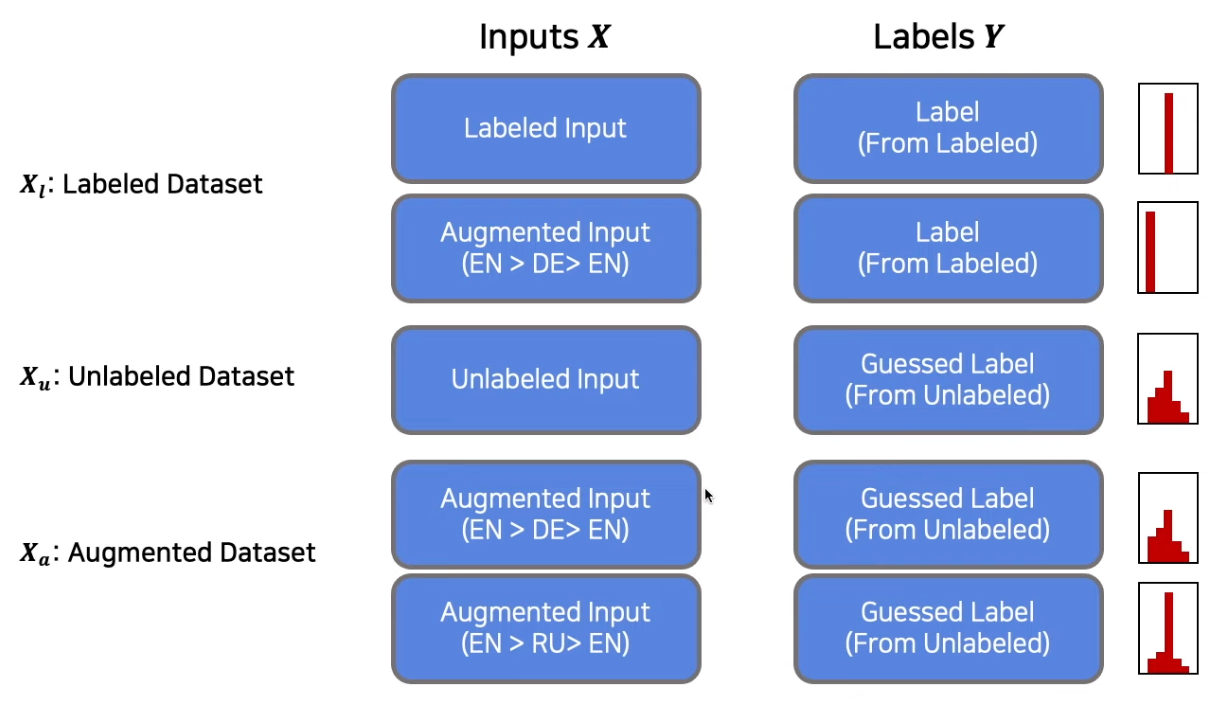
• unlabeled data sample $x_i^u$(원본)와 해당 문장의 증강 버전 $x_{i, k}^a$을 이용하여 label guessing 진행
  • labeled 데이터로 학습한 모델을 이용하여 각각의 예측값(확률값)을 구하고 두 확률의 가중합을 predicted label로 사용

• 위에서 구한 predict label에 sharpening 적용(softmax temperature)
  $\mathrm {Sharpen} (y_i^u, T) = {(y_i^u)^{1\over T} \over \rVert (y_i^u)^{1\over T} \rVert_1}$
  • $\rVert \cdot \rVert_1$ : $l_1$-norm
  • $T \rightarrow 0$이면, 생성된 레이블은 one-hot 벡터로 변형됨

TMix on Labeled and Unlabeled Data

Entropy Minimization

• unlabeled data에 대한 예측값의 확실성을 증가시키기 위해서 엔트로피를 최소화함
• 이를 Loss에 적용하면 아래와 같음
  $L_\mathrm{margin} = \mathbb E_{x \in X_u} \mathrm{max}(0, \gamma - \rVert y^u \rVert_2^2)$
  • $\rVert \cdot \rVert_1$ : $l_1$-norm$\gamma$ = margin hyperparameter
  • 엔트로피가 $\gamma$보다 클 경우에는 엔트로피를 줄이는 방식으로 학습을 진행함

→ 최종 MixText의 objective function

3. MixText의 의의

• 기존 방식(UDA)에서는 labeled와 unlabeled 데이터를 분리해서 모델을 학습해야해서 labeled 데이터에 오버 피팅 될 가능성이 존재함.
• TMix의 경우에는 labeled, unlabeled 데이터 모두 상관 없이 문장을 섞을 수 있고, 무한한 데이터 증강이 가능하기 때문에 오버 피팅의 가능성을 크게 낮출 수 있음