PyTorch Tutorial 05. Logistic Regression

이 글은 한빛미디어의 '김기현의 딥러닝 부트캠프 with 파이토치'를 읽고 정리한 것입니다.

Logistic Regression Model

$n$차원의 실수 벡터를 입력으로 받아 $m$개의 불리언(boolean) 벡터를 반환하는 문제에 적용됩니다. 예를 들어, 키와 몸무게 같은 사람의 신상 정보가 주어졌을 때 성별을 결정하는 모델을 생각해 볼 수 있습니다.

Logistic regression의 경우 출력값이 연속형 데이터에 속하므로 regression으로 분류되지만 이진 분류(Binary Classification)를 다루는데 이용됩니다.

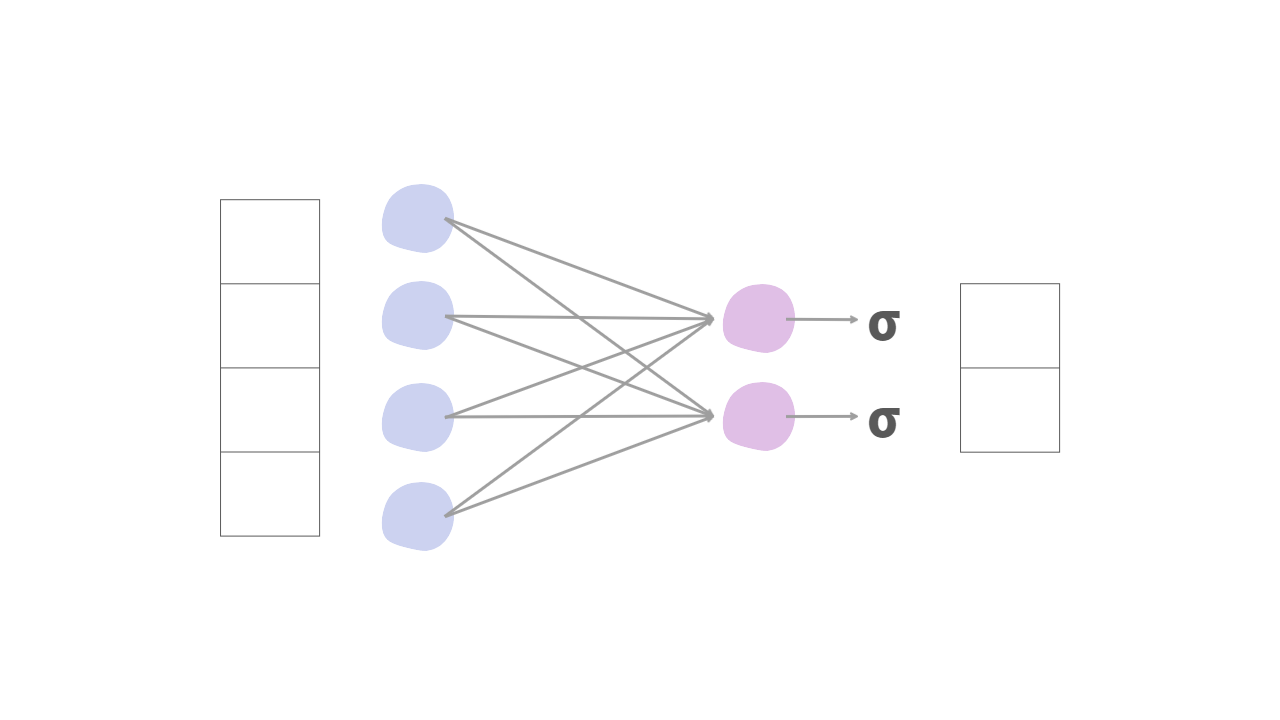
기본 Logistic Regression model은 linear regression 이후에 sigmoid 함수를 추가하여 구성합니다. 그러면 이 모델의 출력값은 0과 1사이로 고정되는데, 이를 활용하여 참/거짓을 예측하는데 사용할 수 있게 됩니다.
0.5를 기준으로 그 이상을 값일 때를 참, 0.5 미만일때 거짓으로 예측하는 모델을 만들 수 있습니다.

이렇게 sigmoid의 출력값을 이용하여 분류 문제를 확률 문제로 접근할 수 있습니다.

Binary Cross-Entropy

기존 회귀 모델(linear regression model)과의 차이 점은 다른 손실함수를 사용하는 것입니다. 이진 분류 문제를 풀기 위해서는 binary cross-entropy를 사용합니다.

PyToch 실습

Dataset

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()

df = pd.DataFrame(cancer.data, columns=cancer.feature_names)
df['class'] = cancer.target
sns.pairplot(df[['class']+list(df.columns[:10])])
plt.show()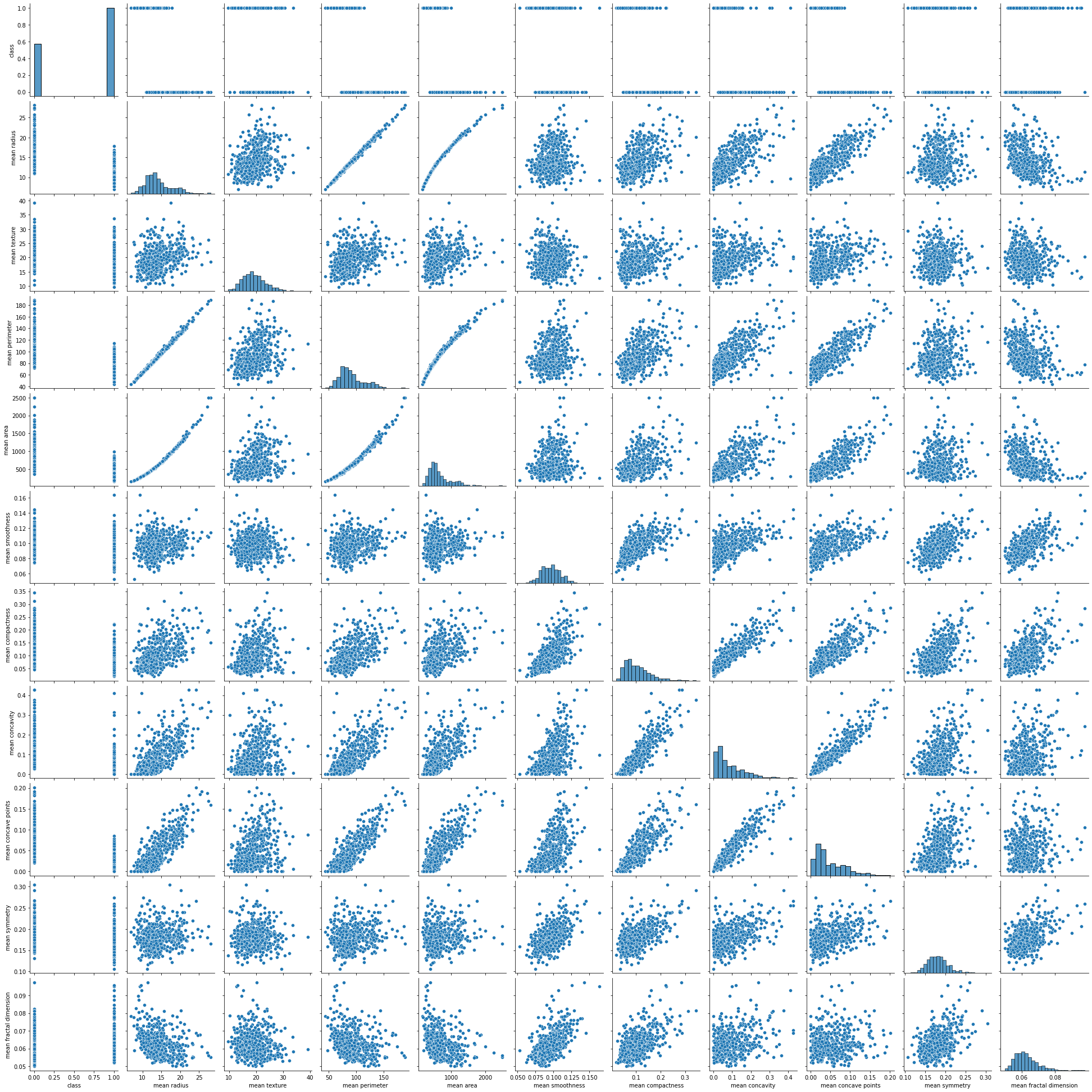

Learning Model 구현

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

data = torch.from_numpy(df[cols].values).float()
data.shape

# split x and y

x = data[:, :-1]
y = data[:, -1:]

print(x.shape, y.shape)

torch.Size([569, 10]) torch.Size([569, 1])

epochs = 200000
lr = 1e-2
print_interval = 10000

class LogisticModel(nn.Module):
  def __init__(self, input_dim, output_dim):
    self.input_dim = input_dim
    self.output_dim = output_dim

    super().__init__()

    self.linear = nn.Linear(input_dim, output_dim)
    self.act = nn.Sigmoid()

  def forward(self, x):
    y = self.act(self.linear(x))
    return y

model = LogisticModel(input_dim = x.size(-1), output_dim = y.size(-1))
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr = lr)

for i in range(epochs):
  pred = model(x)
  loss = criterion(pred, y)

  optimizer.zero_grad()
  loss.backward()
  optimizer.step()

  if (i+1)%print_interval == 0:
    print("Epoch %d: loss=%.4e" %(i+1, loss))

Epoch 10000: loss=2.8316e-01
Epoch 20000: loss=2.3190e-01
Epoch 30000: loss=2.0153e-01
Epoch 40000: loss=1.8186e-01
Epoch 50000: loss=1.6820e-01
Epoch 60000: loss=1.5819e-01
Epoch 70000: loss=1.5054e-01
Epoch 80000: loss=1.4450e-01
Epoch 90000: loss=1.3961e-01
Epoch 100000: loss=1.3557e-01
Epoch 110000: loss=1.3216e-01
Epoch 120000: loss=1.2925e-01
Epoch 130000: loss=1.2674e-01
Epoch 140000: loss=1.2454e-01
Epoch 150000: loss=1.2259e-01
Epoch 160000: loss=1.2087e-01
Epoch 170000: loss=1.1932e-01
Epoch 180000: loss=1.1793e-01
Epoch 190000: loss=1.1666e-01
Epoch 200000: loss=1.1550e-01

결과 확인

correct_cnt = (y==(pred>.5)).sum()
total_cnt=float(y.size(0))

print("Accuracy: %.4f"%(correct_cnt/total_cnt))

Accuracy: 0.9649