PyTorch Tutorial 04. Linear Regression

이 글은 한빛미디어의 '김기현의 딥러닝 부트캠프 with 파이토치'를 읽고 정리한 것입니다.

Linear Regression Model

🦄Regression : Predicting continuous valued output based on past data. cf) classification: Classifying inro different categories

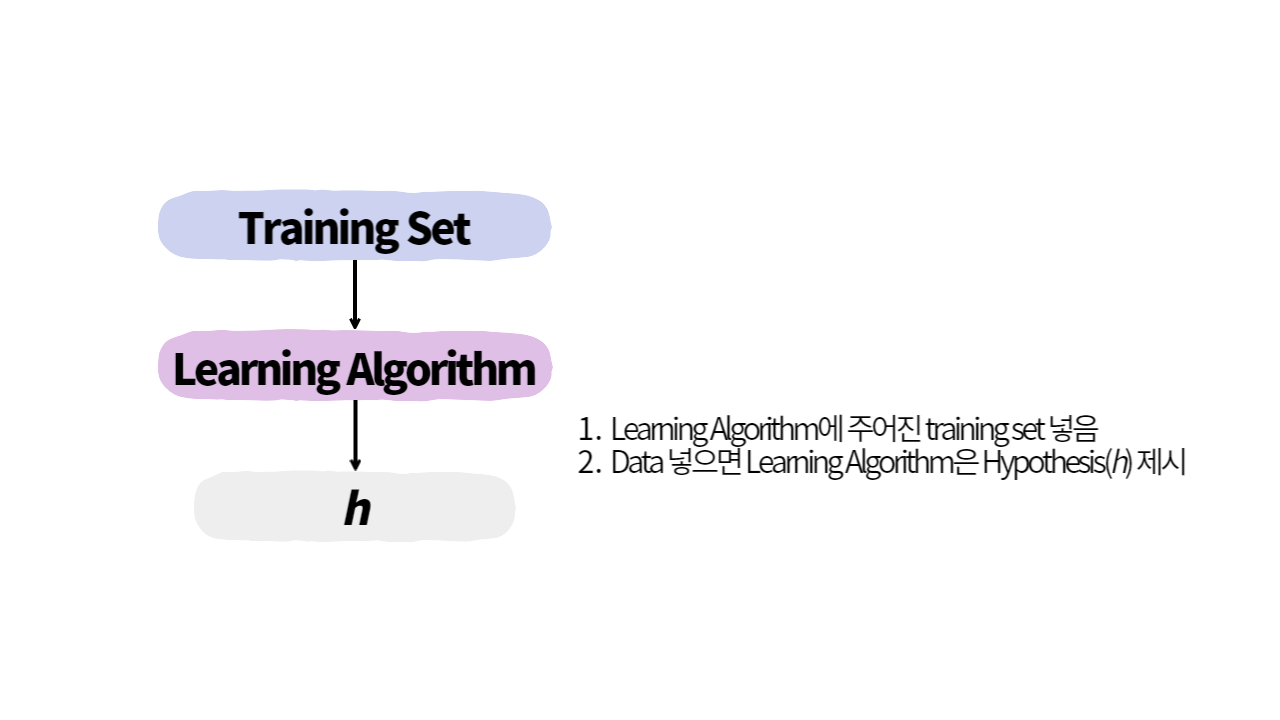
Linear Regression에서 Hypothesis $H(x) = Wx + b$와 같은 형태를 가집니다. 모델 학습으로 $W$와 $b$값을 추론합니다.

모델 학습 과정 N개의 data: input vector(N$\times$n), target vector(N$\times$m)

1. n차원의 input을 선형 회귀 모델에 통과(feed forward)시켜 m차원의 ouput vector($\hat{y}$)를 계산합니다.
2. output vector와 target vector(label)을 비교하여 loss를 구합니다.
3. Gradient descent : loss를 weight parameter로 미분하여 loss를 감소시키는 방향으로 parameter update를 진행합니다.
   $W_{k, j}\gets W_{k, j}-\eta{\partial L(\theta)\over \partial W_{k, j}}$
   $b_j\gets b_j-\eta{\partial L(\theta)\over \partial b_j}$
4. Weight paramter가 수렴할 때까지, 즉 update를 진행해도 값이 변하지않을 때까지 반복하여 loss를 최소화합니다.

Linear Regression 구현하기

import 실습에 필요한 library를 불러옵니다.

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

Dataset 이번 실습에서 용할 dataset인 <보스턴 주탣 가격 데이터 셋>을 불러옵니다. 그리고 간단한 데이터 분석을 진행하기 위해 Pandas Data Frame으로 변환하여 데이터 일부를 확인합니다.

from sklearn.datasets import load_boston

boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df["TARGET"] = boston.target
df.head()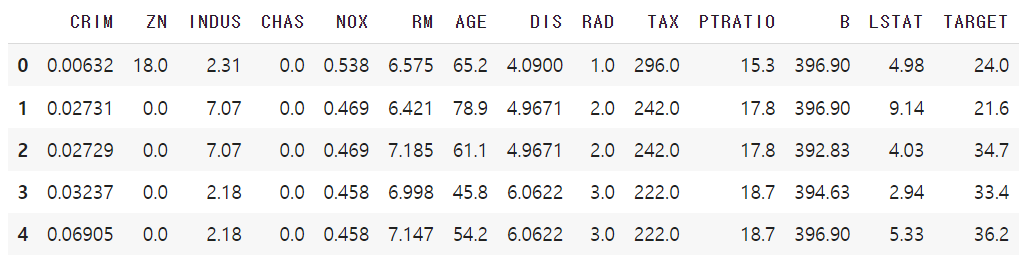

Pairplot을 이용하여 속성의 분포와 속성 사이의 선형적 관계를 파악합니다.

sns.pairplot(df)
plt.show()

약간의 선형적 관계를 가지는 일부 속성을 추려내어 pairplot을 그립니다.

cols = ["TARGET", "INDUS", "RM", "LSTAT", "NOX", "DIS"]
sns.pairplot(df[cols])
plt.show()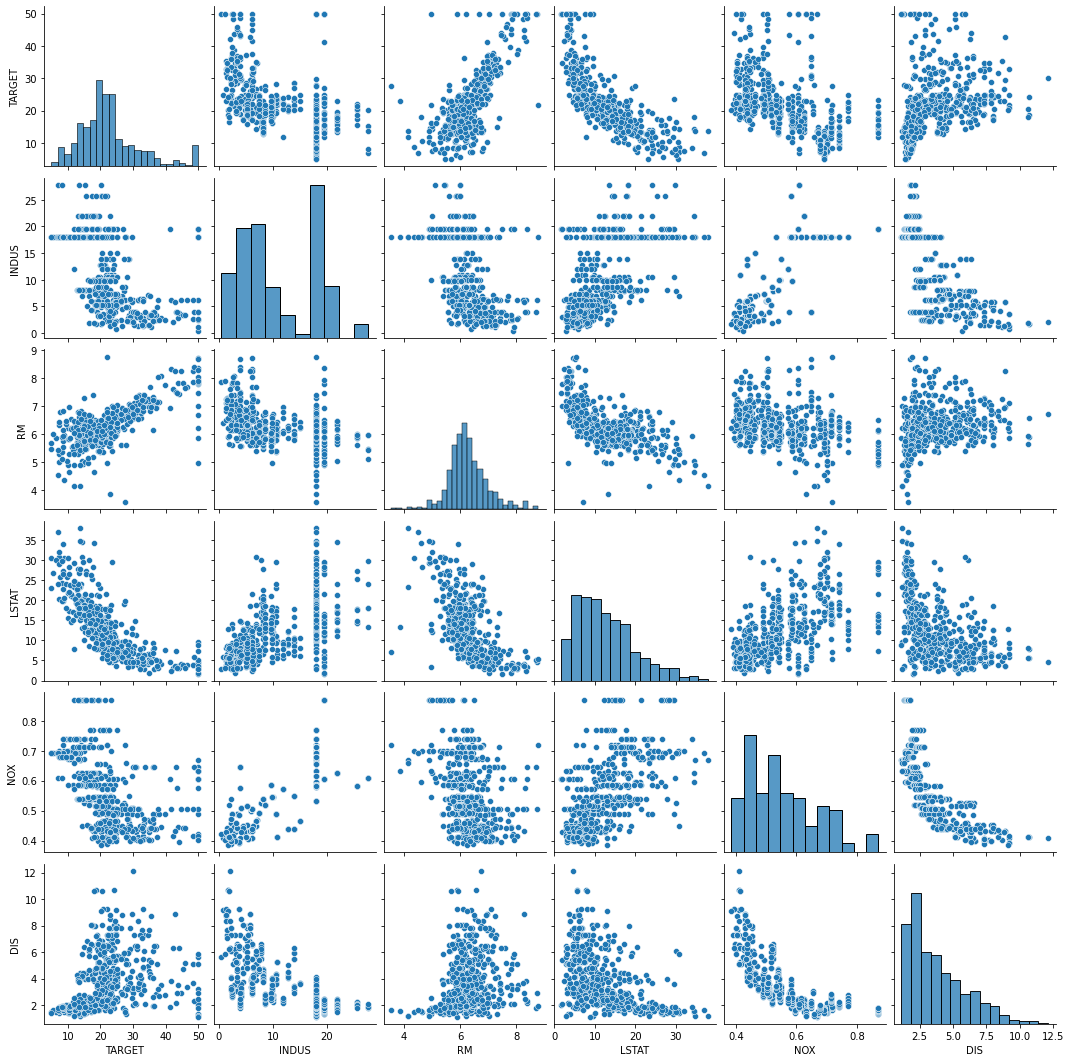

학습 코드 구현
위의 과정을 통해 추려낸 numpy 데이터를 실수형(float) tensor로 변환합니다.

data = torch.from_numpy(df[cols].values).float()
data.shape

[out] torch.Size([506, 6])

그리고 input $x$와 target $y$로 나눕니다. 이때, INDUS, RM, LSTAT, NOX, DIS가 input vector $x$의 features이며, tensor 데이터에서 첫 번쩨 열이 각 데이터들의 target(label)입니다.

x = data[:, 1:]
y = data[:, :1]
x.shape, y.shape

[out] torch.Size([506, 5]), torch.Size([506, 1]))

학습에 필요한 설정값인 epochs, learning rate 등을 정의하고 model을 생성합니다.

epochs = 2000
lr = 1e-3
print_interval = 100

선형 회귀 모델을 구현할 것이므로 nn.Linear을 이용합니다.

model = nn.Linear(x.size(-1), y.size(-1))
model

[out] Linear(in_features=5, out_features=1, bias=True)

이전 게시물 Gradient Descent & AutoGrad에서는 직접 경사하강법을 구현했는데, 해당 작업은 torch에서 제공하는 optimizer 클래스를 이용하여 수행할 수 있습니다.
optimizer = torch.optim.(최적화에 이용할 경사하각 모델)([최적화 대상 parameter], learning rate)

optimizer = optim.SGD(model.parameters(), lr = lr)

for i in range(epochs):
  y_pred = model(x)
  loss = F.mse_loss(y, y_pred)

  optimizer.zero_grad()
  loss.backward()
  optimizer.step()

  if (i + 1) % print_interval == 0:
    print("Epoch %d: loss=%4e" %(i+1, loss))

Epoch 100: loss=4.245179e+01
Epoch 200: loss=3.648206e+01
Epoch 300: loss=3.321451e+01
Epoch 400: loss=3.137279e+01
Epoch 500: loss=3.033455e+01
Epoch 600: loss=2.974912e+01
Epoch 700: loss=2.941887e+01
Epoch 800: loss=2.923245e+01
Epoch 900: loss=2.912707e+01
Epoch 1000: loss=2.906737e+01
Epoch 1100: loss=2.903341e+01
Epoch 1200: loss=2.901396e+01
Epoch 1300: loss=2.900269e+01
Epoch 1400: loss=2.899602e+01
Epoch 1500: loss=2.899195e+01
Epoch 1600: loss=2.898935e+01
Epoch 1700: loss=2.898757e+01
Epoch 1800: loss=2.898626e+01
Epoch 1900: loss=2.898521e+01
Epoch 2000: loss=2.898431e+01

optimizer.zero_grad()가 필요한 이유
Pytorch는 미분을 통해 얻은 기울기를 이전에 계산된 기울기 값에 누적시키는 특징 있음. 따라서 optimizer.zero_grad()를 통해 미분값을 0으로 초기화해주어야 함.

결과 확인

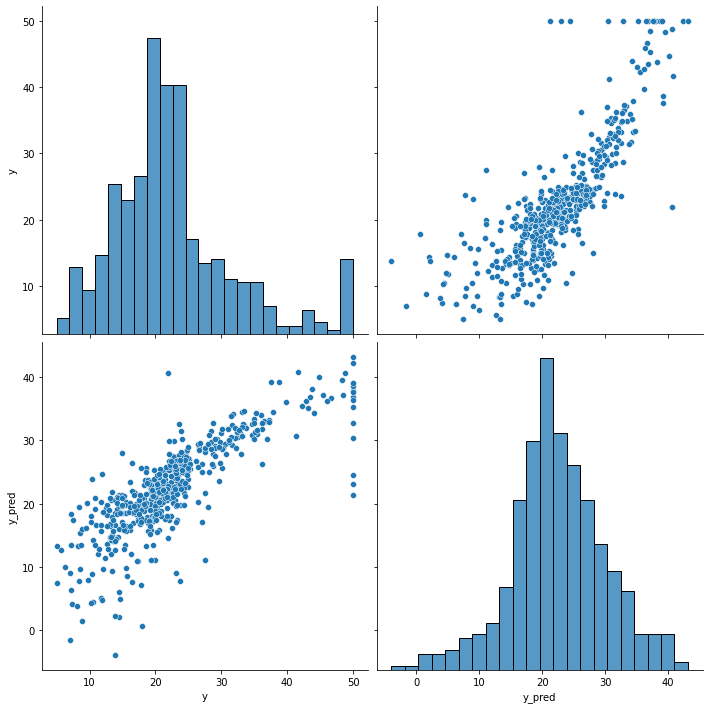
df = pd.DataFrame(torch.cat([y, y_pred], dim = 1).detach_().numpy(), columns = ["y", "y_pred"])
sns.pairplot(df, height = 5)
plt.show()