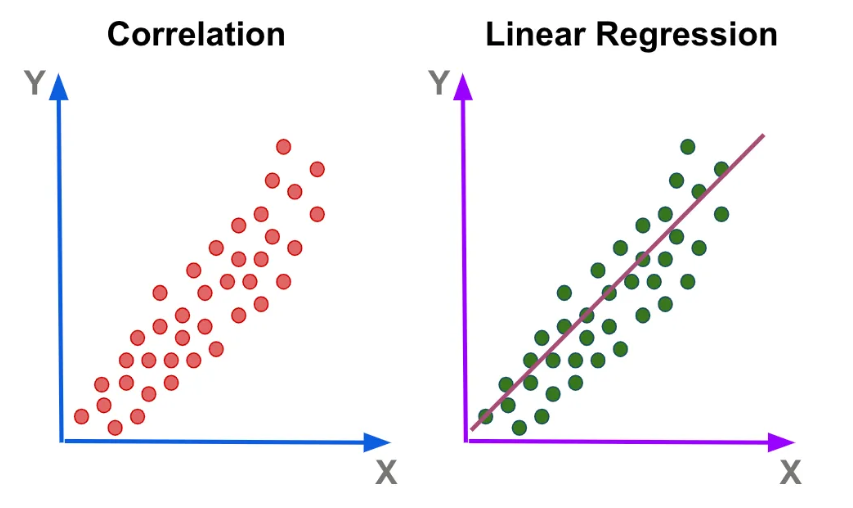
1. Linear Regression
예측 문제
기존 데이터를 기반으로 새로운 데이터에 대한 종속변수 값을 예측
(독립 변수와 종속 변수 간 관계식을 알고있으면 새로운 독립 변수에 대한 종속 변수 예측 가능)
가중치 (Weight)
- 독립 변수의 중요도를 부여하거나 단위를 바꾸기 위한 변수
- 독립 변수와 종속 변수 간의 관계를 정의하는 변수
편향 (bias)
독립 변수의 편향(전반적인 값)을 조절하기 위한 변수
2. Cost Function
모델의 성능을 측정하는 함수 (예측값과 실제값 차이를 측정, 차이가 곧 비용)
- 일반적으로 평균 제곱 오차(MSE, Mean Squared Error) 함수를 사용하여 비용 측정

3. Optimization
목적을 달성하기 위한 최적의 parameter ( ) 를 찾는 과정
- 목적 : 독립 변수와 종속 변수 사이의 관계를 잘 설명하는 모델 만들기
- 목표 : 비용 최소화
학습(Training) : 어떤 알고리즘을 통해 스스로 최적의 값을 찾아나가는 과정
Linear Regression의 최적화
선형 회귀 모델의 에 따른 비용특성을 알아야 최적화 가능함.
-
(Weight)와 간 특성 그래프
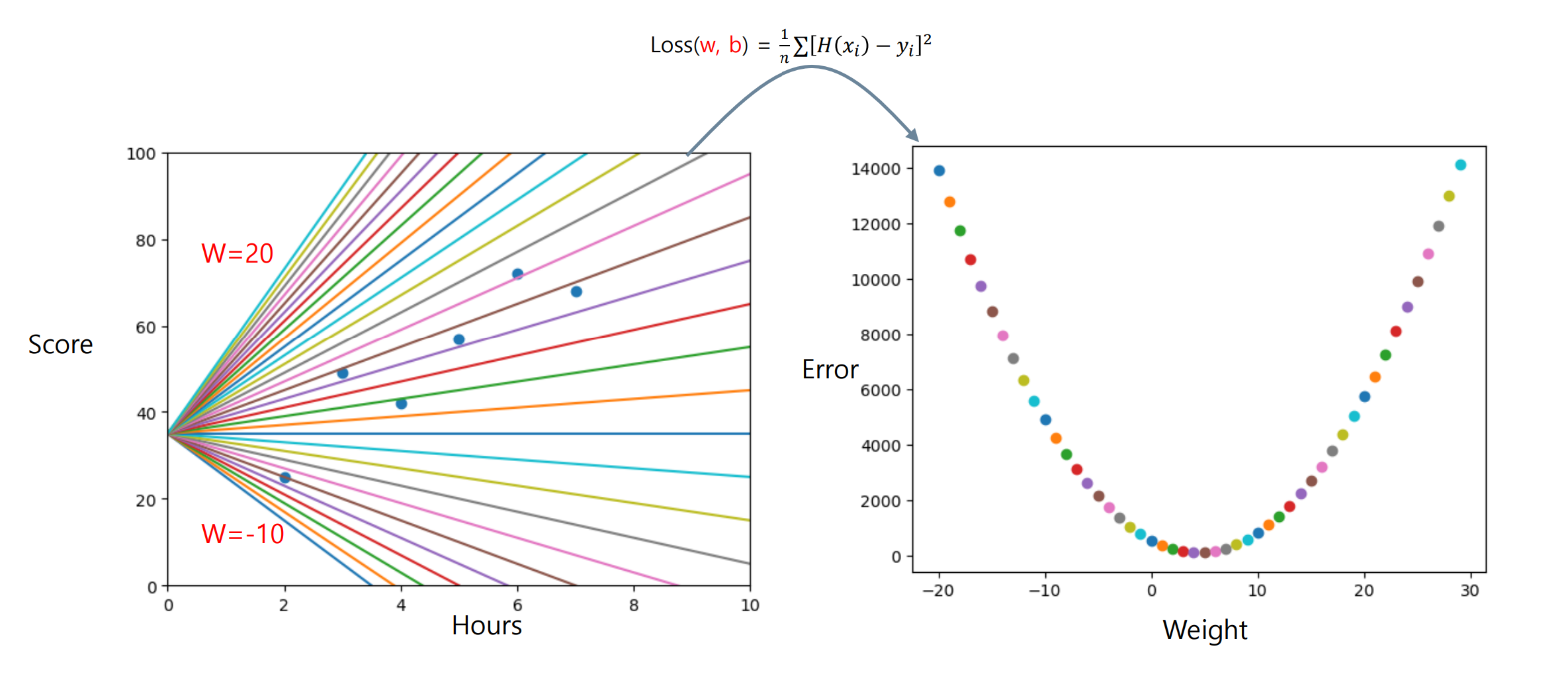
-
(Bias)와 간 특성 그래프
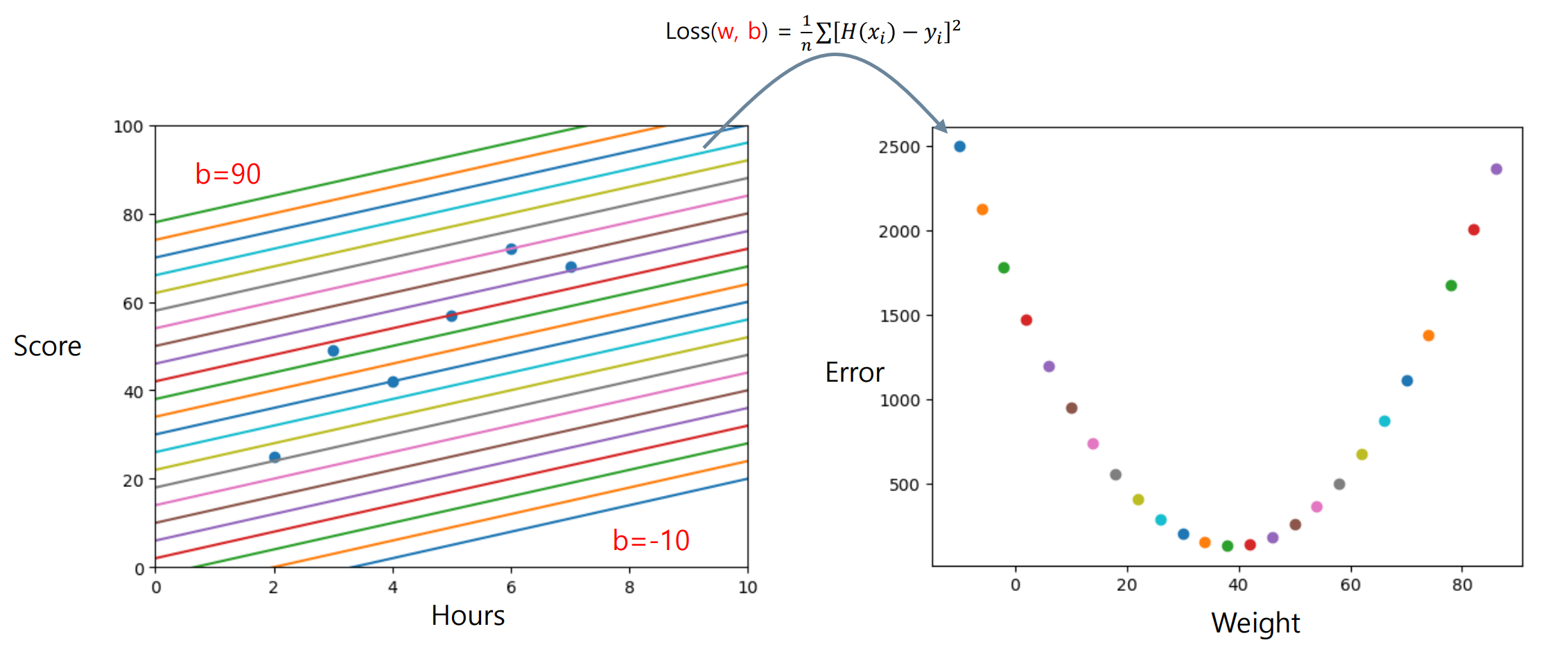
4. Gradient Descent
함수의 기울기를 이용하여 함수의 최솟값을 찾는 방법
- 함수의 기울기는 편미분을 통해 구함 (Gradient Descent를 통해 최적의 값으로 update)
= cost function이 MSE이기에 이차 방정식의 최소를 구하는 방법과 유사

Cost가 가장 최소인 지점은 기울기가 0이되는 지점으로, 이 부분이 최적의 값이다.
이때 기울기가 0이 되는 지점을 기준으로 왼쪽에는 음수, 오른쪽에는 양수가 된다.
Gradient Descent(경사하강법)의 정의
update를 하면서 기울기가 0이 될 때까지 경사하강법을 실행
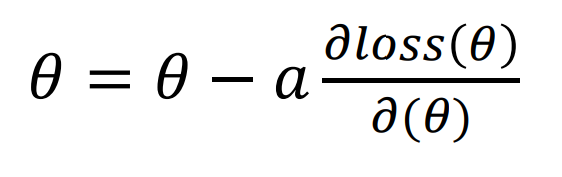
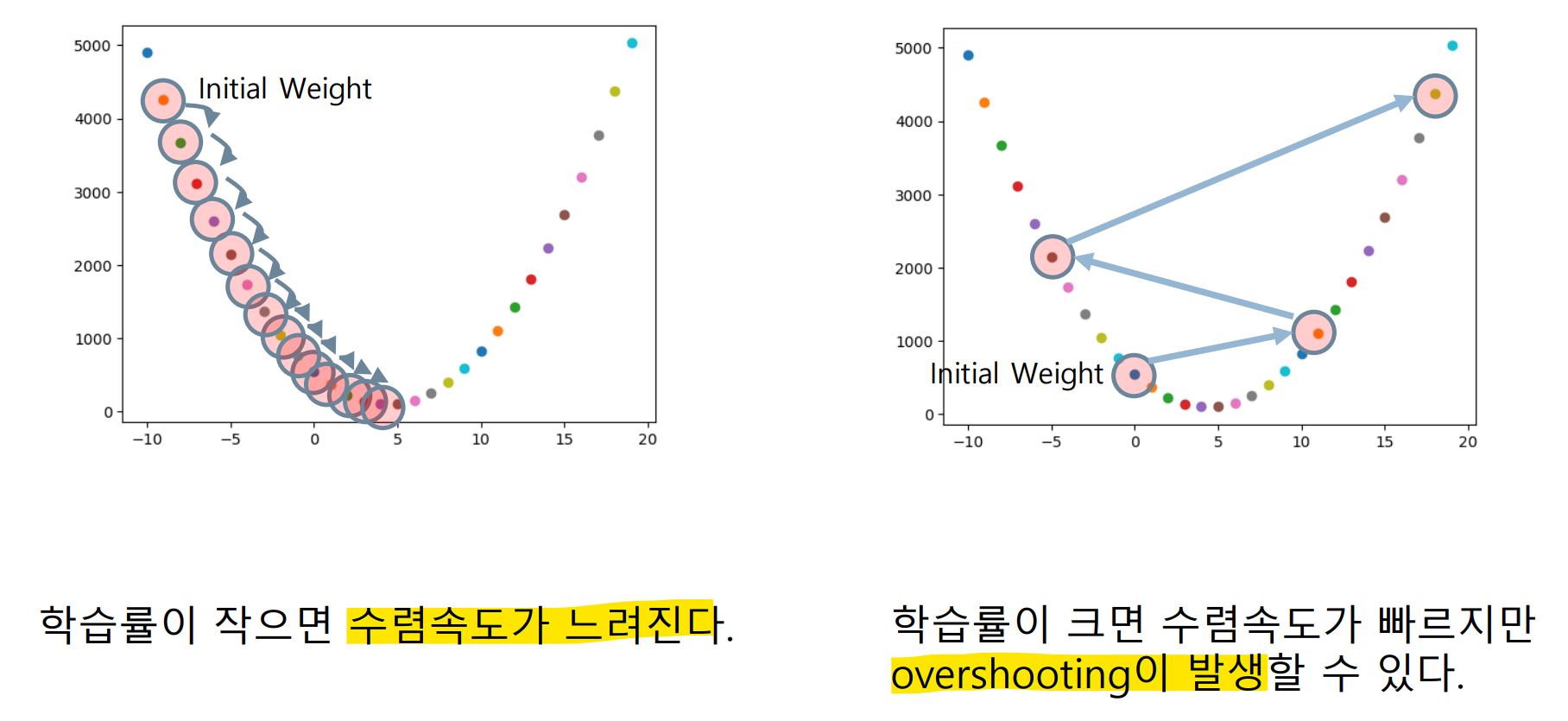
Learning rate(학습률)
경사하강법의 이동거리를 조절하는 값 (error를 고치는 방향으로 얼마만큼 이동할지 결정)
- Learning rate가 낮으면 수렴속도가 낮아짐(비효율적)
- Learning rate가 높으면 Overshooting 발생(발산)
5. Derivative
python code로 Gradient Descent를 구현하려면 미분이 된 식을 작성해야된다.
하지만 python에는 미분과 관련된 식이 없기에, 편미분 한 상태의 식을 바로 적어야 한다.
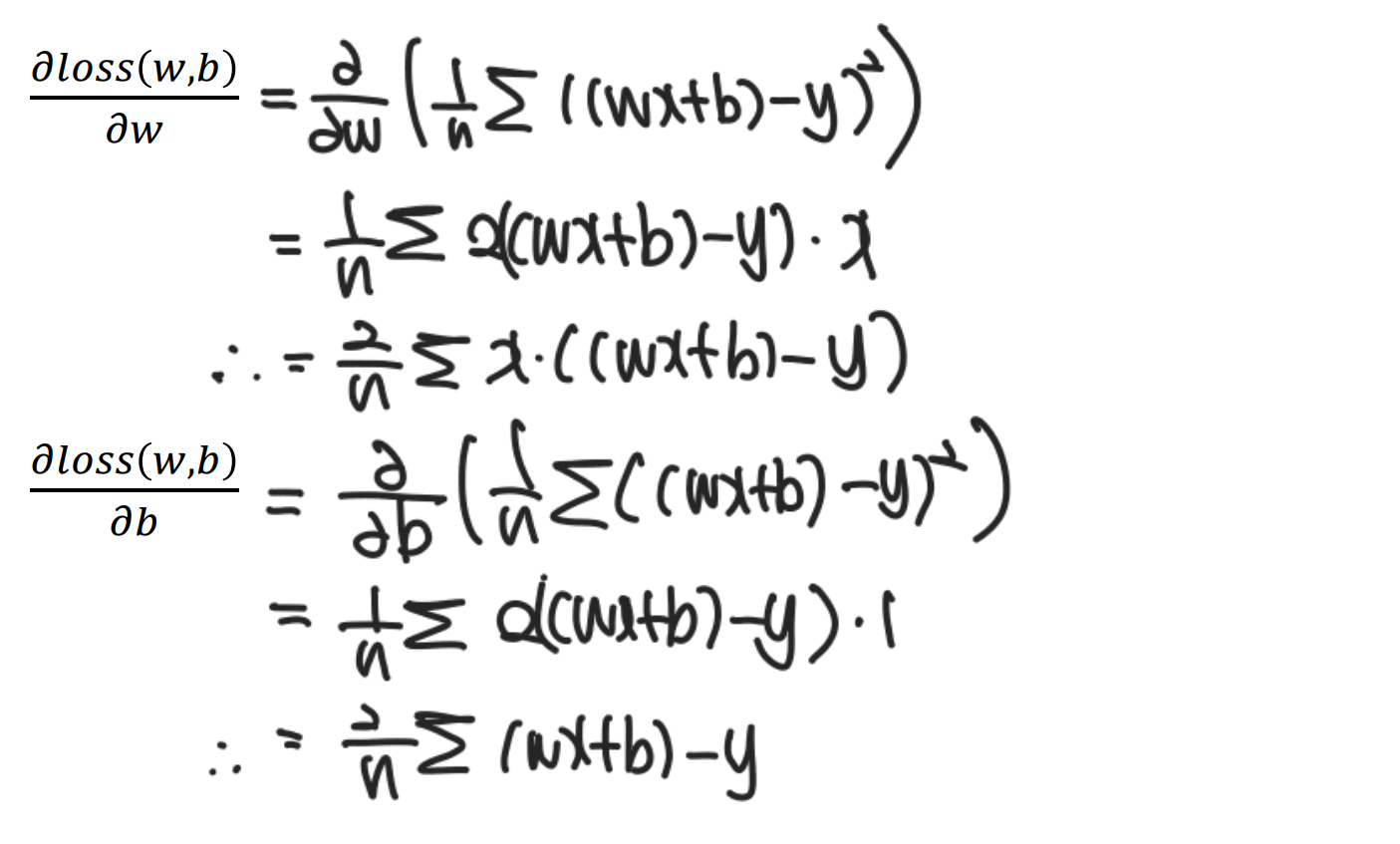
6. Linear Regression 실습
: Linear Regression Hard Coding / Using Sklearn
Hard Coding
import numpy as np
import matplotlib.pyplot as plt
#dataset
score=np.array([25, 49, 42, 57, 72, 68])
hours=np.array([2,3,4,5,6,7])
hours_=np.r_[0, hours, 10]
#hyperparameter
lr=0.001
epochs=10000
n=hours.shape[0]
#initialize
w=np.random.uniform()
b=np.random.uniform()
w_init=w
b_init=bdef hypothesis(x,w,b):
return w*x+b
for epoch in range(epochs):
h=hypothesis(hours, w, b)
loss=np.mean((h-score)**2)
dw=(2/n)*sum(hours*(h-score))
db=(2/n)*sum(h-score)
w=w-lr*dw
b=b-lr*db
print(loss)
print(w,b)
h=w*hours_+b
h_init=w_init*hours_+b_init
plt.scatter(hours, score)
plt.plot(hours_, h)
plt.plot(hours_, h_init)
plt.show()
Using Sklearn
import matplotlib.pyplot as plt
from sklearn import linear_model
reg=linear_model.LinearRegression()
score=[25, 49, 42, 57, 72, 68]
hours=[[2],[3],[4],[5],[6],[7]]
hours_=[[0],[2],[3],[4],[5],[6],[7],[10]]
reg.fit(hours, score)
print(reg.coef_, reg.intercept_)
y_pred=reg.predict(hours_)
plt.scatter(hours, score)
plt.plot(hours_, y_pred)
plt.show()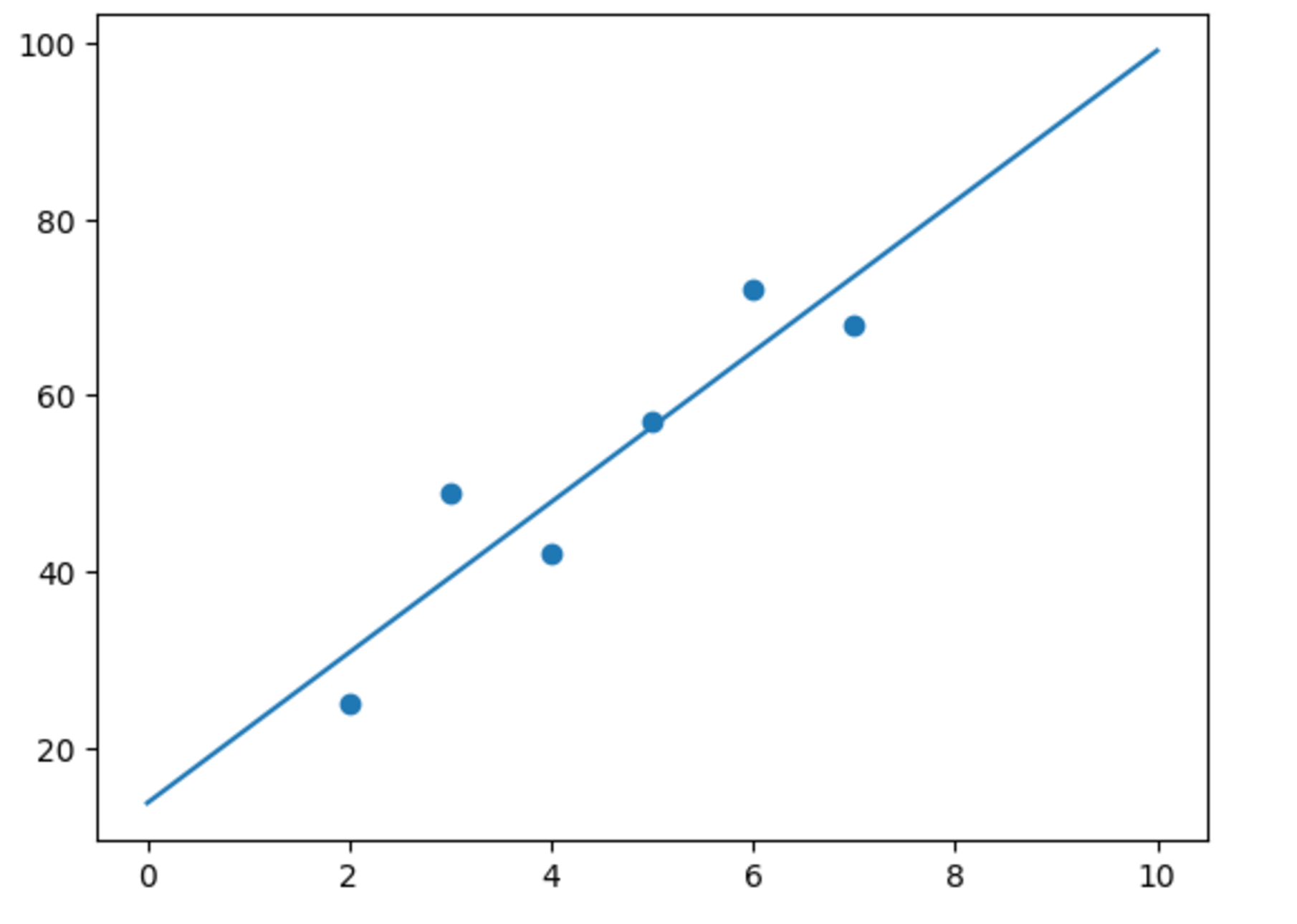
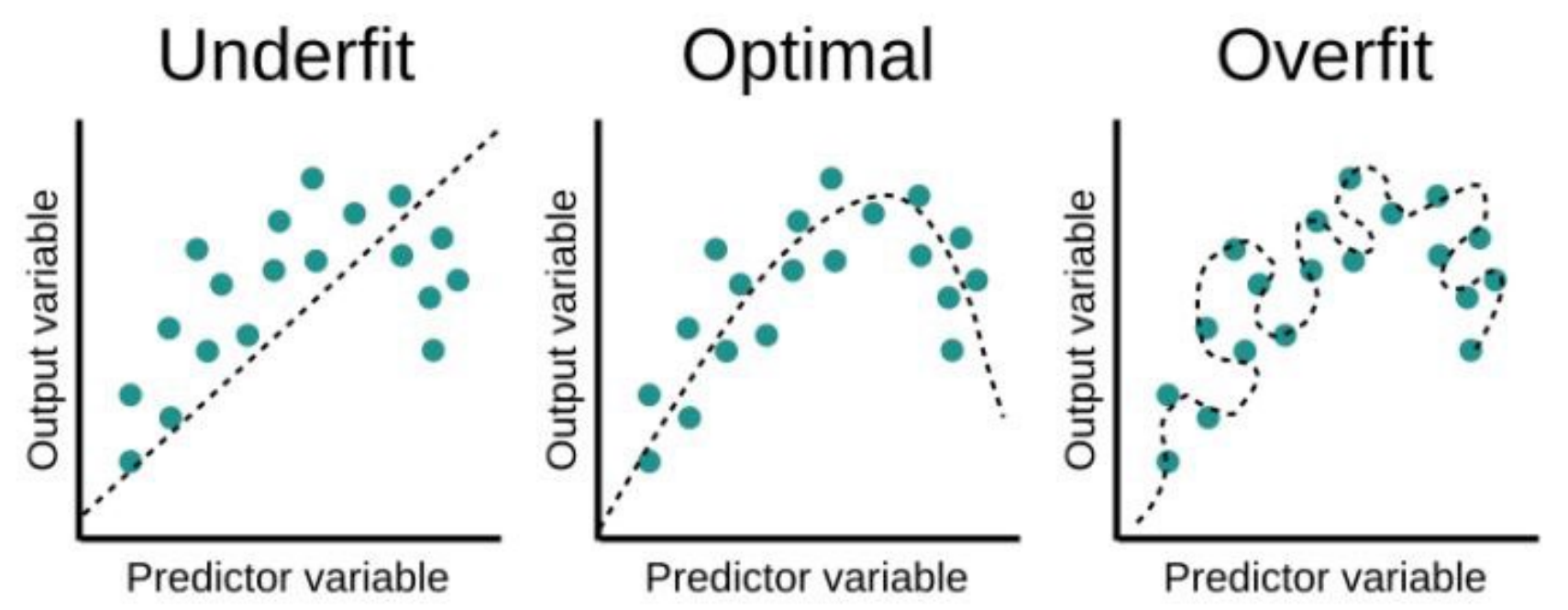
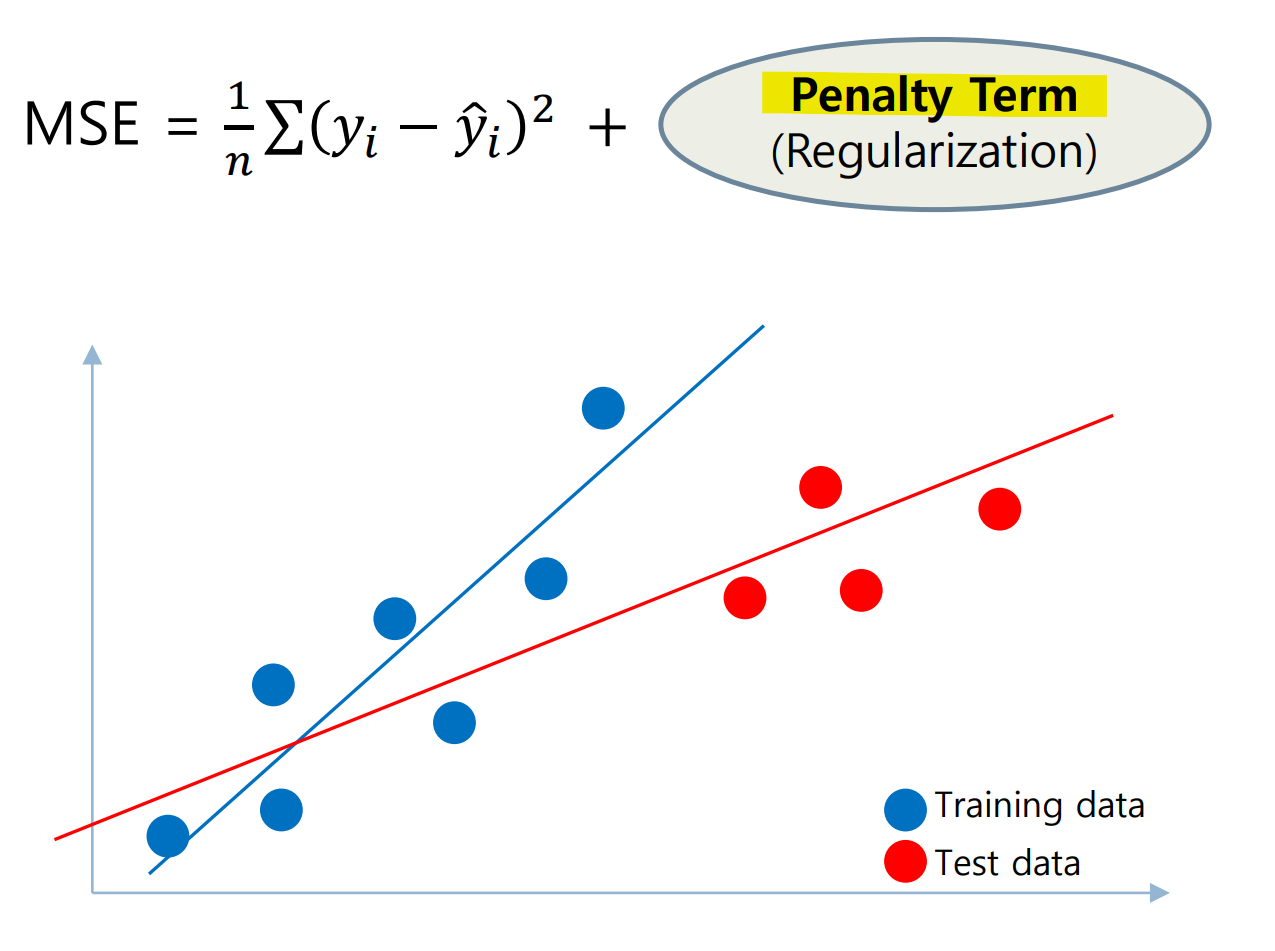
Overfitting vs Underfitting
Overfitting : train data가 과도하게 학습되어 test data의 성능이 떨어지는 경우
Underfitting : train data에서 조차 학습이 잘 안 되어 성능이 떨어지는 경우
7. Regularization
Linear Regression은 모델이 복잡해질 수록 Train data에 대한 정확도가 높아진다.
하지만 너무 Model Complexity가 높을 수록 낮은 테스트 성능을 보여주는 Overfitting 상태가 되므로, 모델을 단순화 시키는 과정을 통하여 튜닝할 필요가 있다.
Parameter ()에 따른 손실함수 특성 분석
- 값이 클 수록 Low bias, High variance -> overfitting 될 수도 있음
- 값이 작을 수록 High bias, Low variance -> underfitting 될 수도 있음

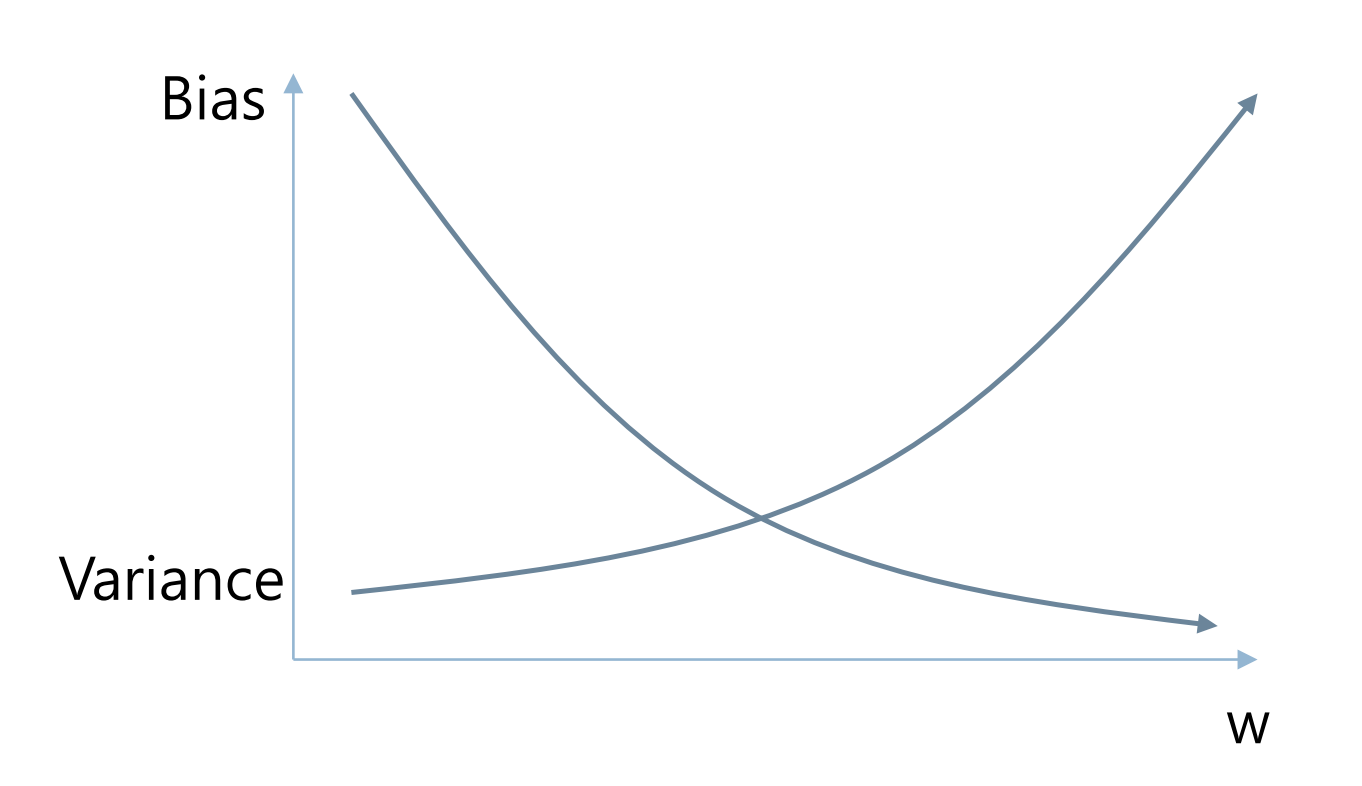
Bias-Variance trade-off
에 따른 손실함수 특성 분석을 통해 bias와 variance가 trade off된다는 것을 확인할 수 있음.
Overfitting을 유도하고 값을 작게 만들어 문제 해결해야 됨
Regularization
모델 학습 시 손실 함수(Loss function)에 페널티 항(penalty term)을 추가하여 모델이 과대 적합되지 않도록 하는 것
값이 커질 수록, penalty term이 커지기에 loss 값이 커짐
(model이 값이 커지는 것을 최대한 피해서 update 하게 됨)
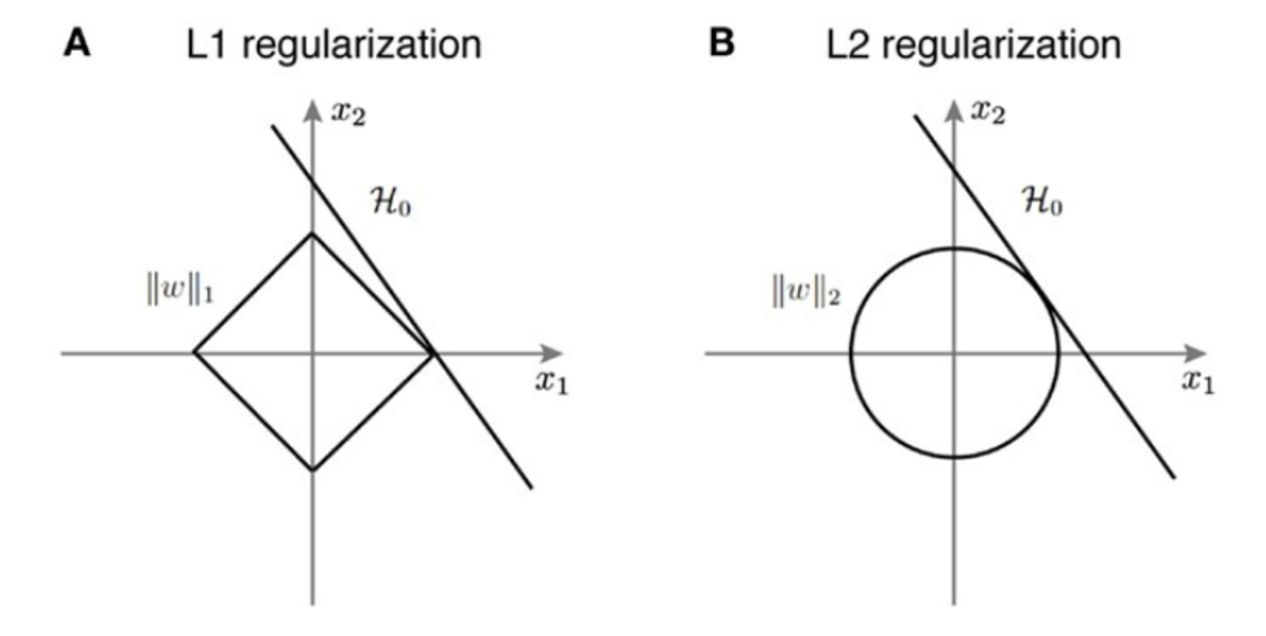
- L1 (Lasso Regularization)
- L2 (Ridge Regularization)
L1 (Lasso Regularization)
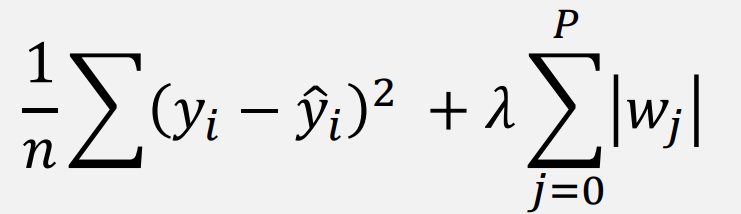
- 일부 가중치를 0으로 설정하여 모델의 복잡도를 줄이는 효과 있음
- 고차원 데이터에서 불필요한 특성을 제거한 모델 제공 가능
(미분 불가능, 절댓값이기에)
L2 (Ridge Regularization)
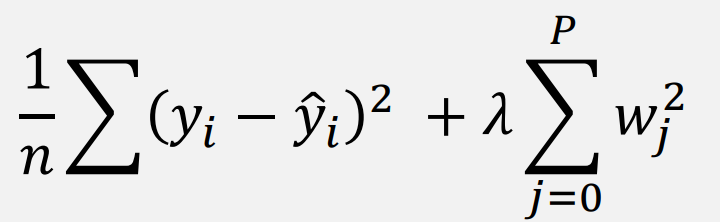
- 모든 를 작게 만들지만, Lasso와 달리 0으로 설정하지는 않음
- 상관관계가 높은 변수들을 적절히 조정하여 모델 안정성을 높임
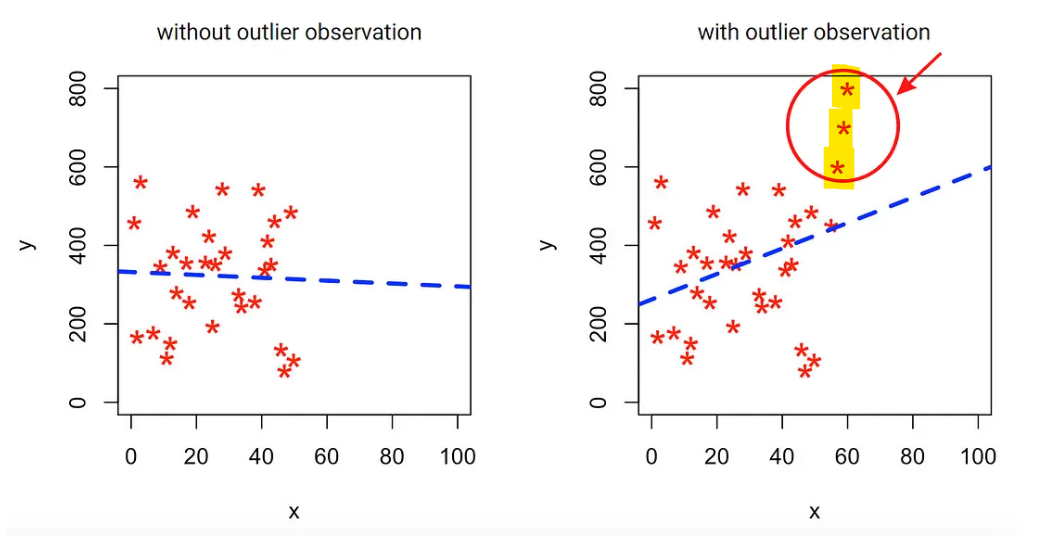
Outlier
이상치로, 다른 관측값들과 크게 다르거나 극단적으로 벗어난 값을 의미
Linear Regression에서는 outlier가 model에 중대한 영향을 끼침
(이상치의 영향을 받아 fitting line이 이동, 성능 저하 발생)
사진 출처
원인 : 데이터 입력 오류/시스템 오류(센서 이상)/특이한 값
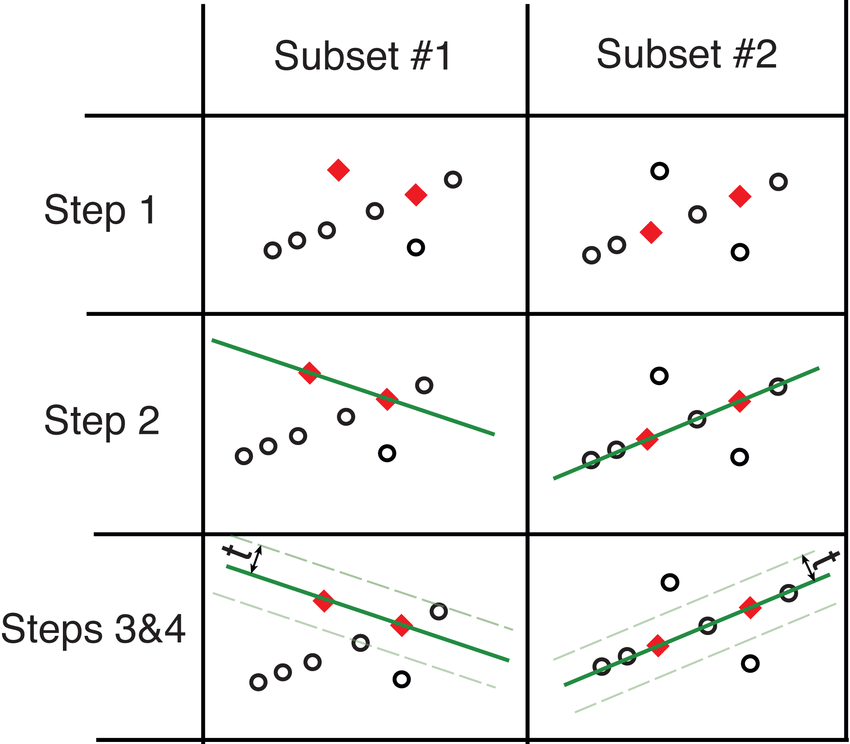
8. RANSAC
Random Sample Consensus(RANSAC)으로 이상치의 영향을 최소화하면서 모델을 학습하기 위해 만들어진 알고리즘
응용 분야
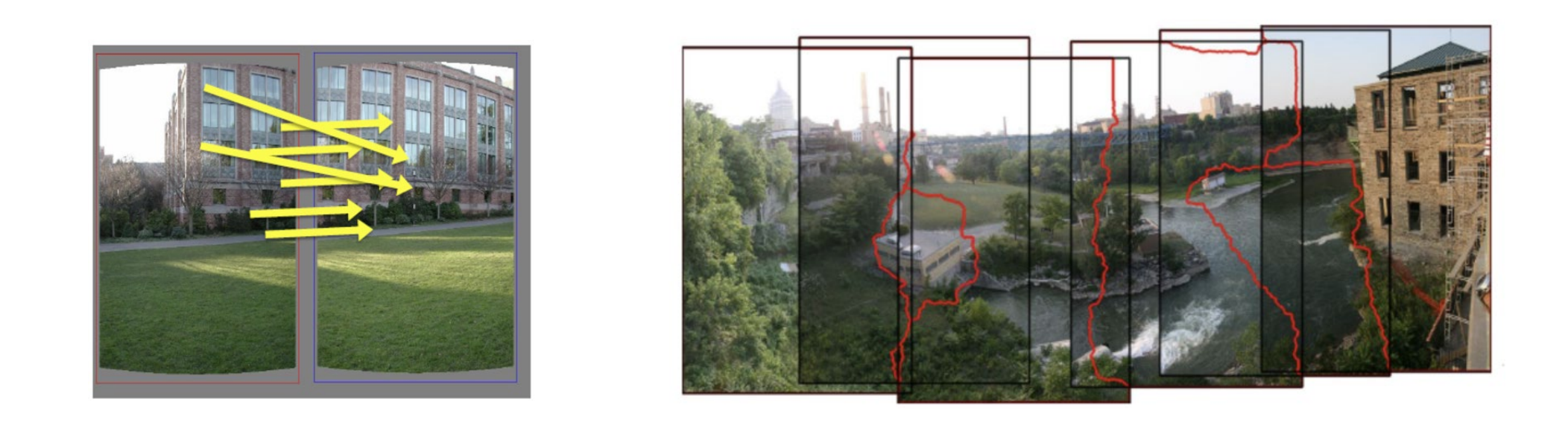
- Model Fitting : 이상치가 많은 데이터를 기반으로 하는 선형 회귀 모델 생성
- Computer Vision : 이미지 간 특징 매칭 (변환 행렬 추정)
Step 1. 모델 초기화
전체 데이터에서 임의의 데이터를 선택하여 초기 모델 생성
( 개의 데이터로 Fitting Line 만들 수 있음)
- 다음 예시의 경우, 로 임의의 두 데이터를 선택한 것임
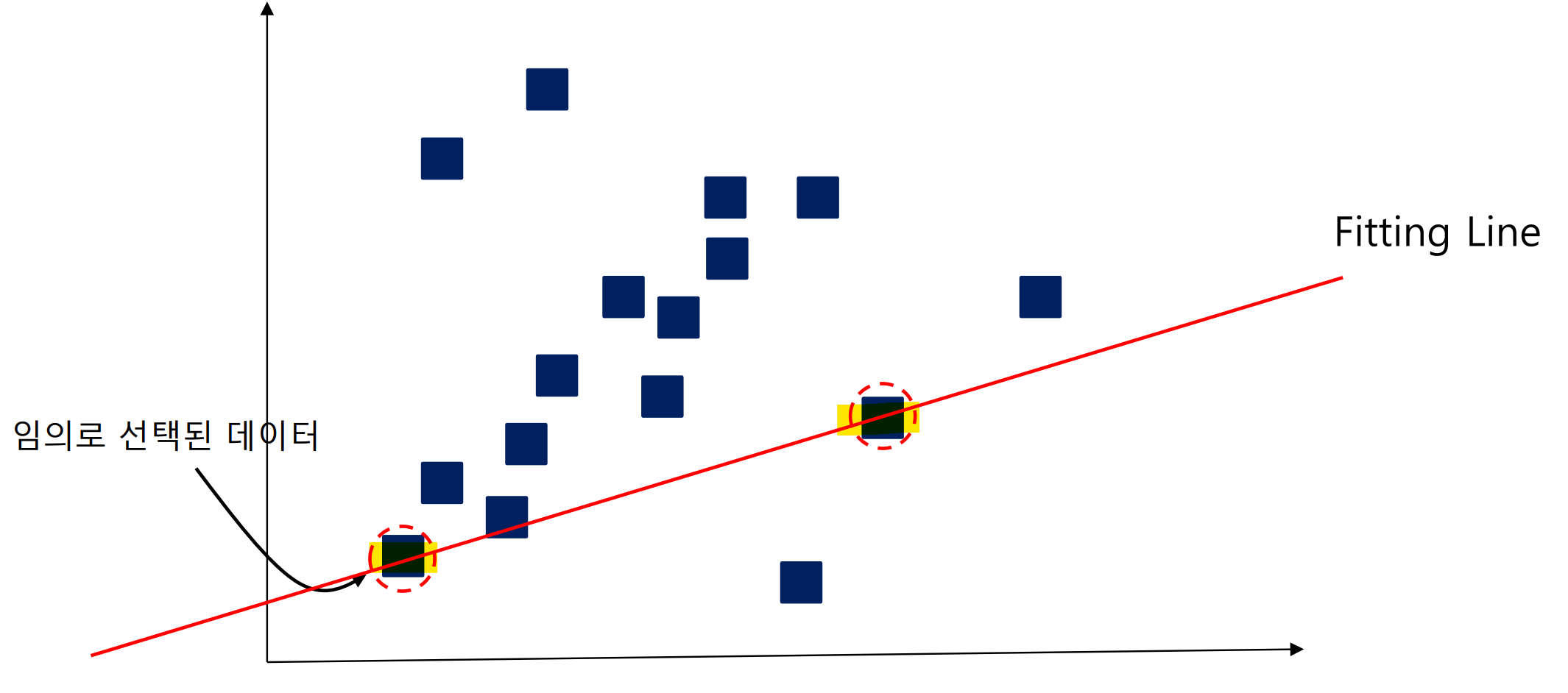
Step 2. 모델 평가
생성된 모델을 기반으로 허용오차(Threshold) 범위에 있는 내부치(Inlier)를 찾음
평가는 전체 데이터 중 fitting line 안에있는 데이터의 비율로 평가
- 다음 예시의 경우, Fitting line에 있는 Inlier 5개, 전체 데이터 16개
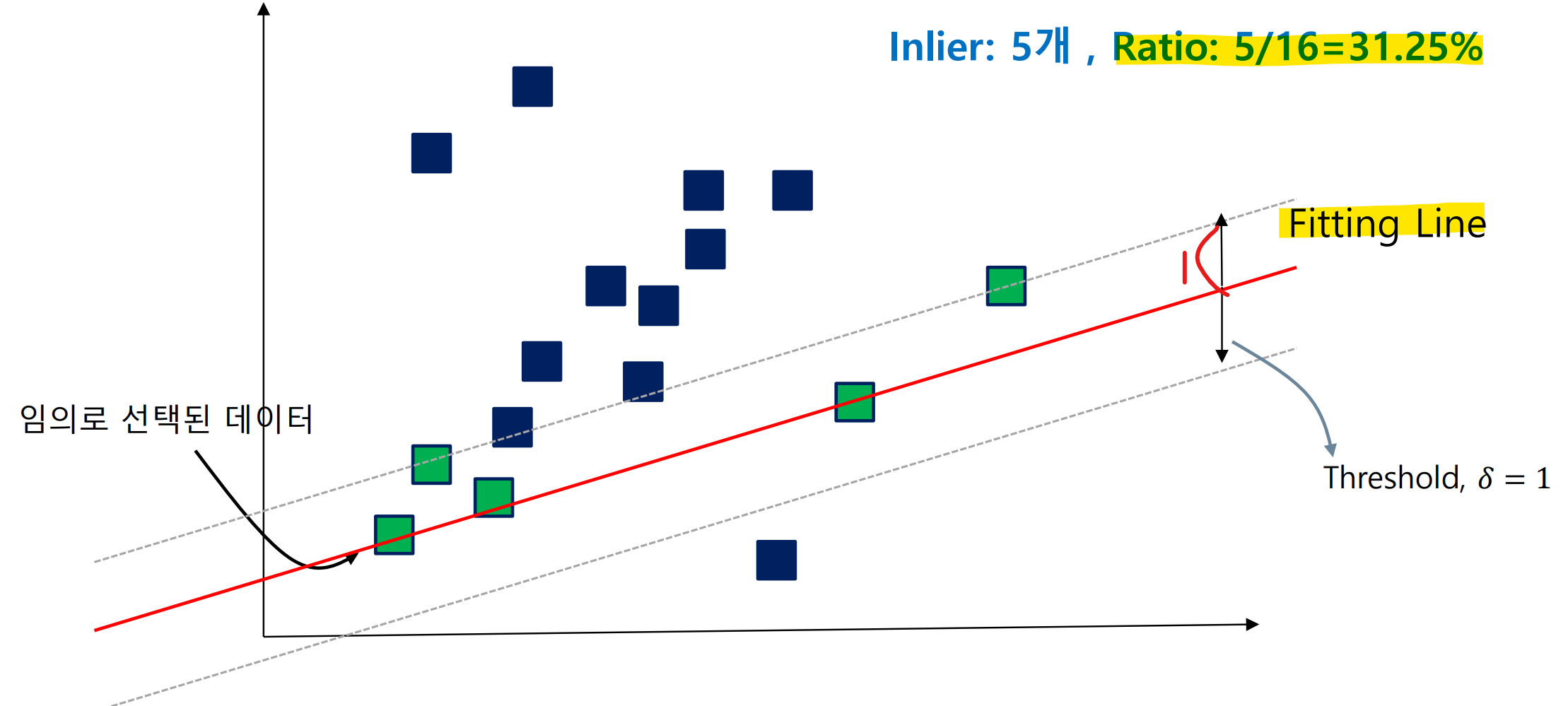
Step 3. 최적화
step 1,2의 과정을 최적의 모델 찾을 때까지 반복
만약 평가 기준이 이전 model보다 낮으면 기록 X / 높으면 기록하고 update
-
ratio가 이전 모델보다 낮아서 기록하지 않는 경우
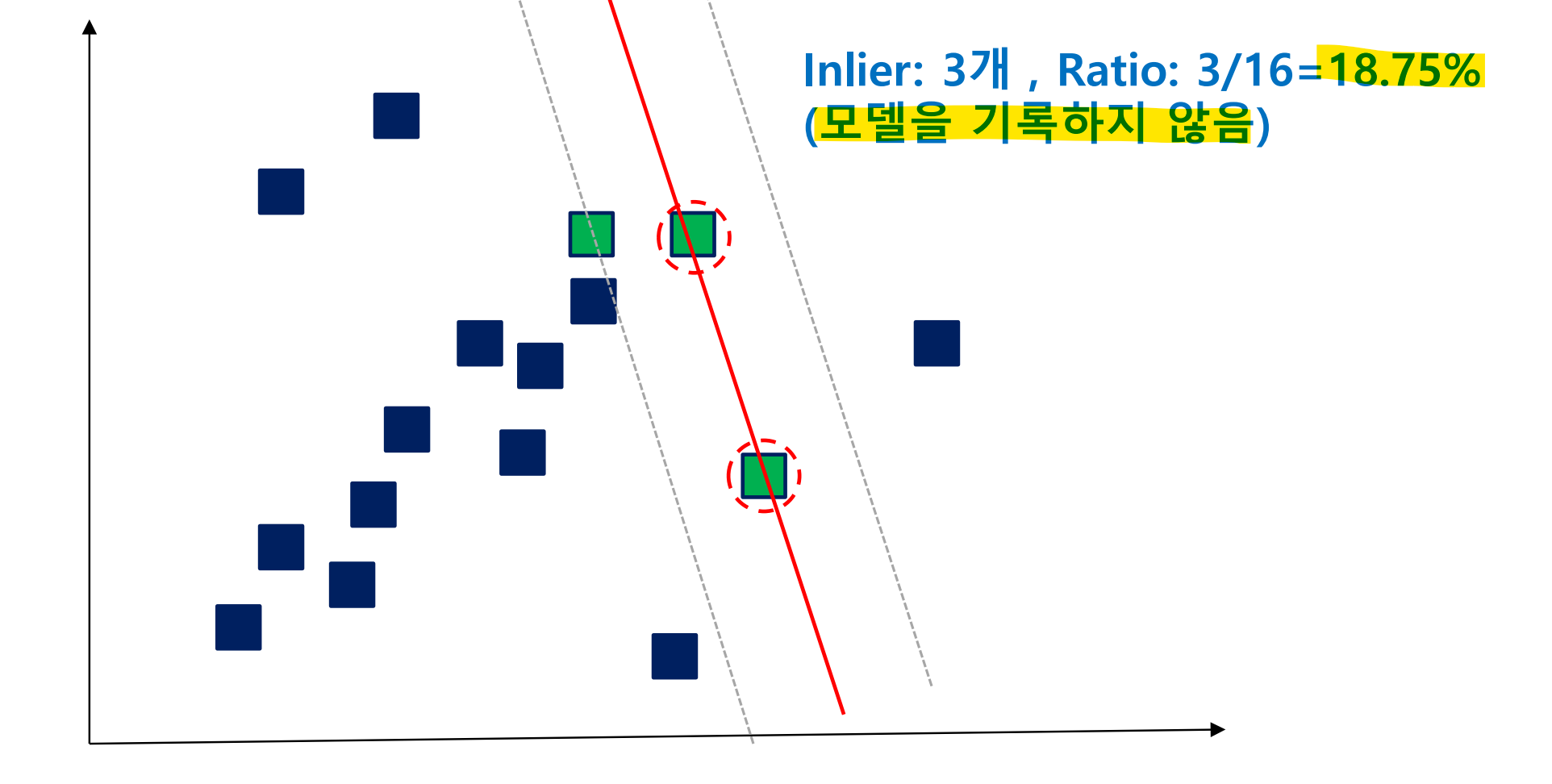
-
ratio가 이전 모델보다 높아서 기록하고 update하는 경우
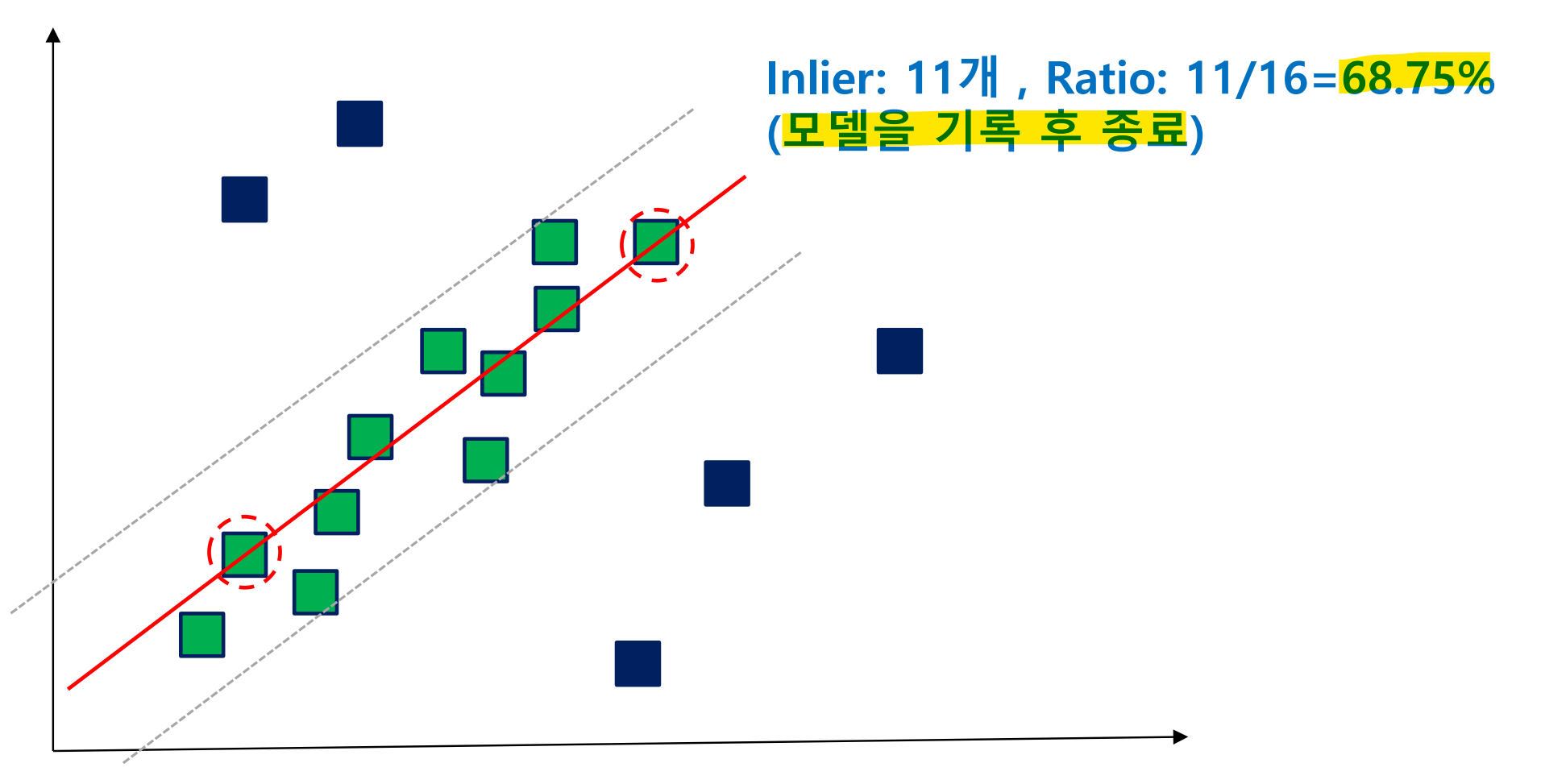
RANSAC 동장방식 예시
9. RANSAC 최적화
: RANSAC 논문의 Question으로, '최적의 모델을 위해 몇 번 반복해야될까?'
RANSAC에서 최적의 모델 모습은 내부치 만을 포함하는 데이터를 선택하여 학습할 때이다.
이때, 확률적으로 몇 번 시도하면 내부치만을 포함하는 샘플이 선택될까?