Heuristic Search Techniques 한계
-
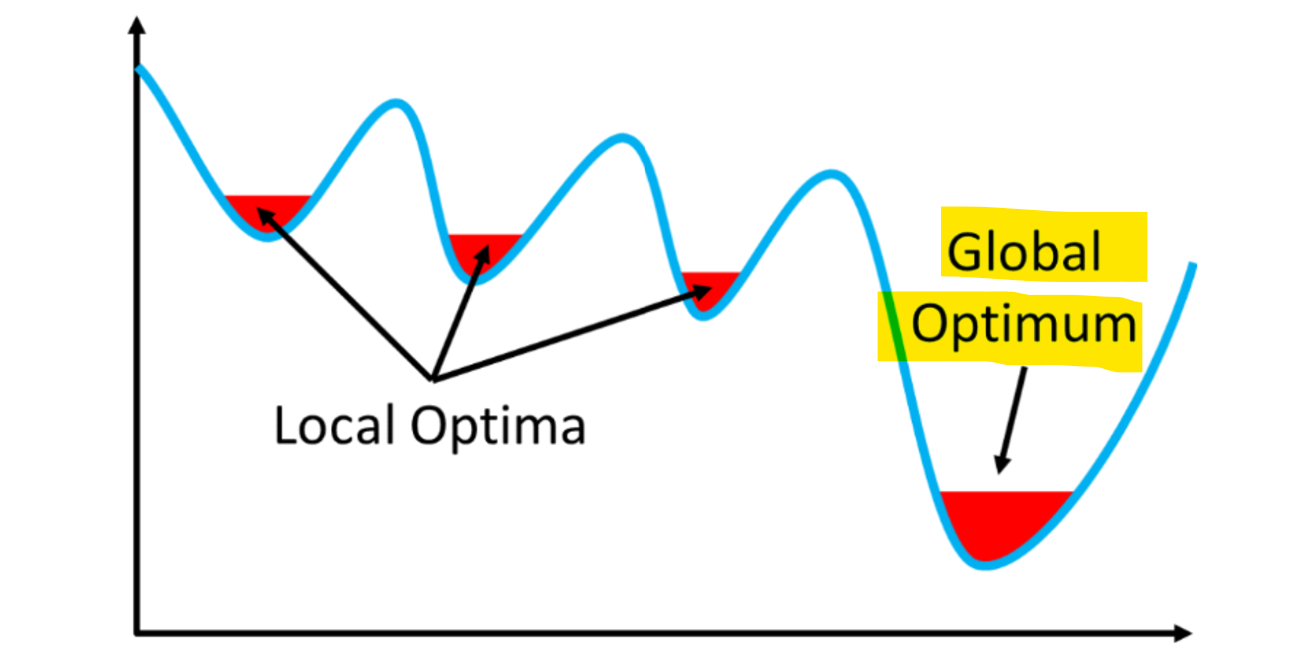
local minima 문제
최적의 해를 구하지 못했지만, 최적이라고 판단하여 탐색을 종료 -
시스템 최적화 문제
하나의 시스템은 연속적인 단일 변수만 존재하는 것이 아니라 discrete, categorical, integer, boolean 등 다양한 변수가 복합적으로 존재
(다변수 시스템에서 모든 변수의 최적의 해를 찾는 것은 어려운 일)
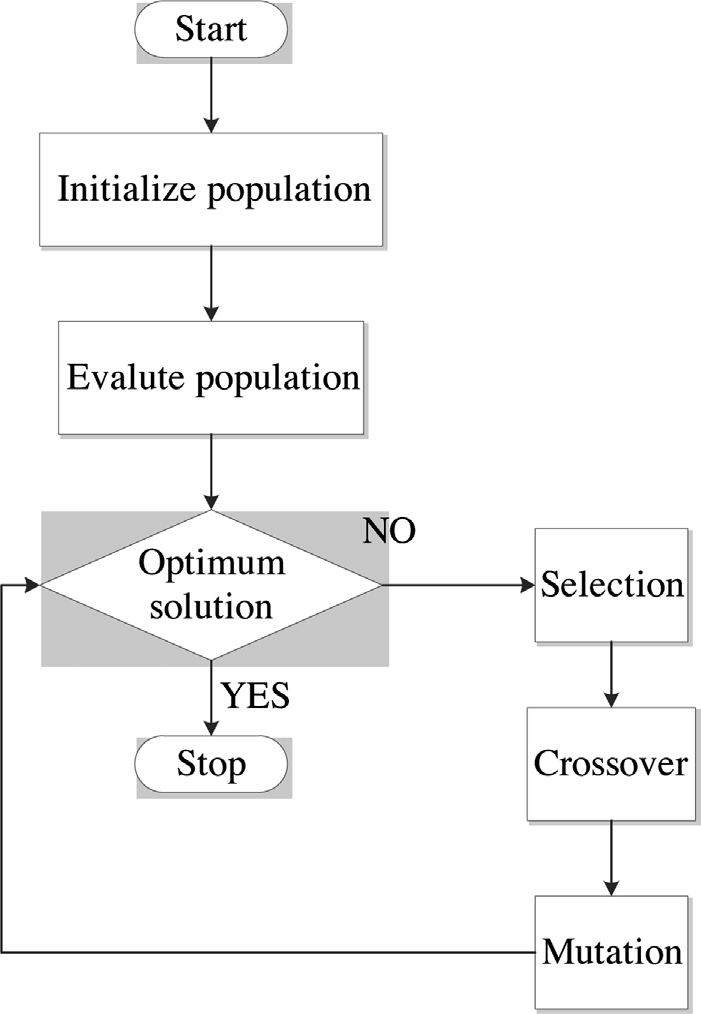
1. Genetic Algorithm 배경
생물체의 염색체가 유전되는 현상에서 영감을 얻은 최적화 알고리즘
교차, 돌연변이, 토대 등의 과정을 통하여 우성 유전자만이 살아남는 자연계의 현상을 알고리즘으로 만든 것
(명확하게 정의되지 않은 문제에도 적용할 수 있기에 다양한 응용에서 매우 활발히 이용)
GA terminology
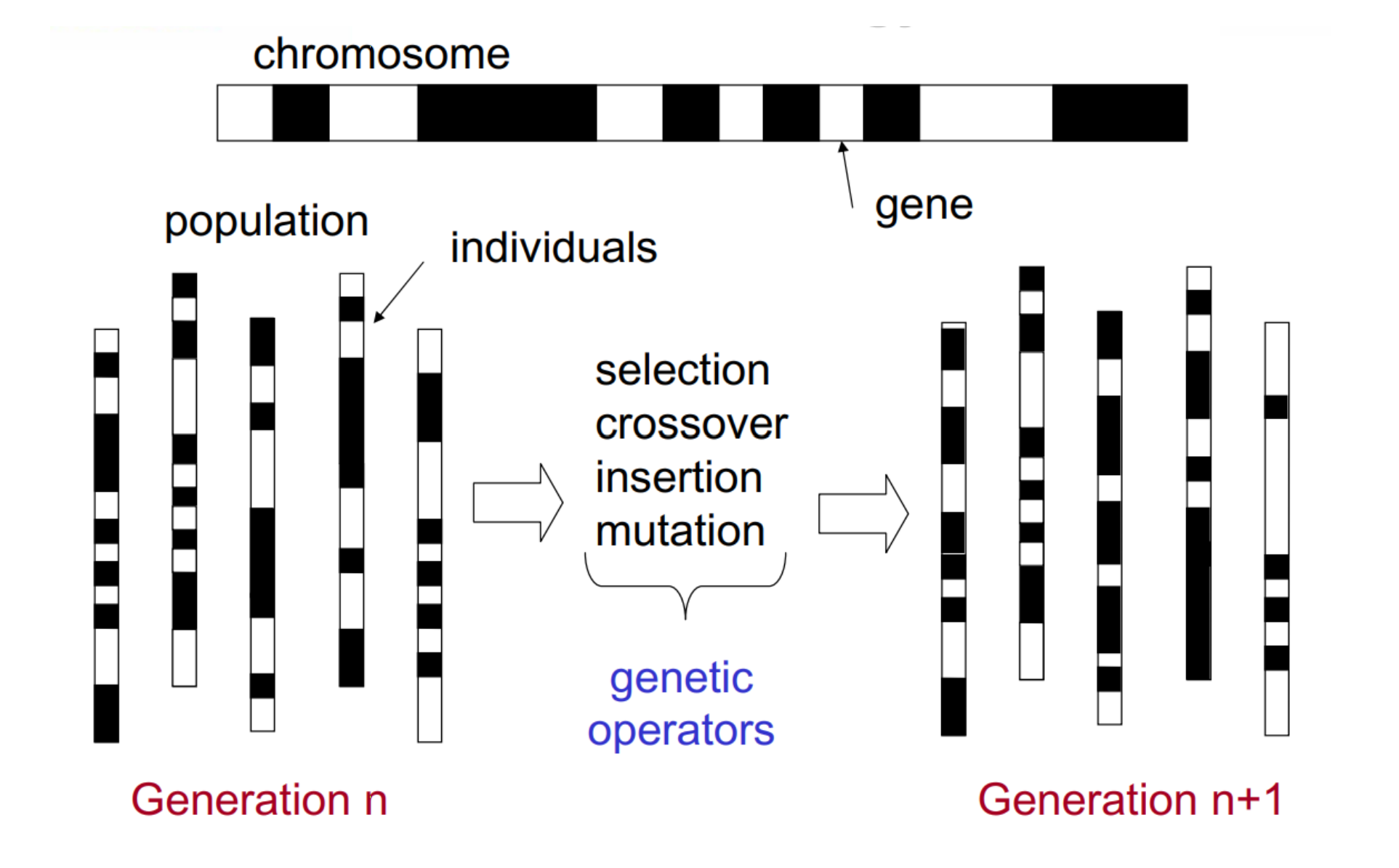
- Chromosome(염색체) : 생물학적으로는 유전 물질을 담고 있는 하나의 집합을 의미하며, 유전 알고리즘에는 하나의 해(solution)를 표현
- Gene(유전자) : 염색체를 구성하는 요소로써, 하나의 유전 정보를 나타냄
- Fitness(적합도) : 어떠한 염색체가 갖고 있는 고유값으로써 해당 문제에 대해 염색체가 표현하는 해가 얼마나 적합한지를 나타냄
Chromosomes
보통의 경우 염색체의 bit는 0 또는 1로 표현 (유전자 하나를 의미)
주어진 염색체의 유전자를 실제 어떤 값으로 표현하는 것을 Encoding이라 함
(-> 염색체는 Encoding된 정보이기에 Decoding 필요)
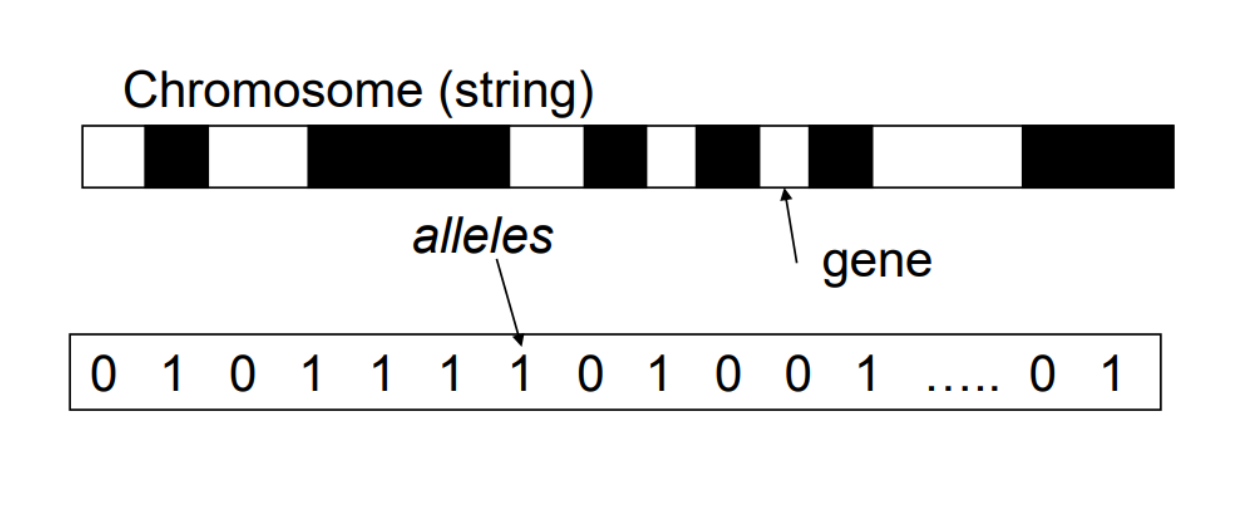
Encoding Schemes
유전 뿐만 아니라 다양한 최적화 문제에 사용되기에 Genetic Algorithm Encoding에는 여러가지 종류 있음
( task에 따라 scheme도 달라짐 )
feature selection에는 주로 binary encoding 사용
- binary alphabet { 0, 1 } (일반적인 Schemes)

사진 출처 - One-hot encoding : { 0, 1, 2, ... , 25 } ; { A, B, C, ... , Z }
2. Genetic Algorithm
GA Step 1. Initialization
Encoding Chromosomes
GA 알고리즘은 유전 뿐만 아니라, 다양한 최적화 문제에 사용되기에 다양한 Encoding Scheme가 사용되지만,
일반적으로 feature selection에서는 Binary Encoding이 사용된다.
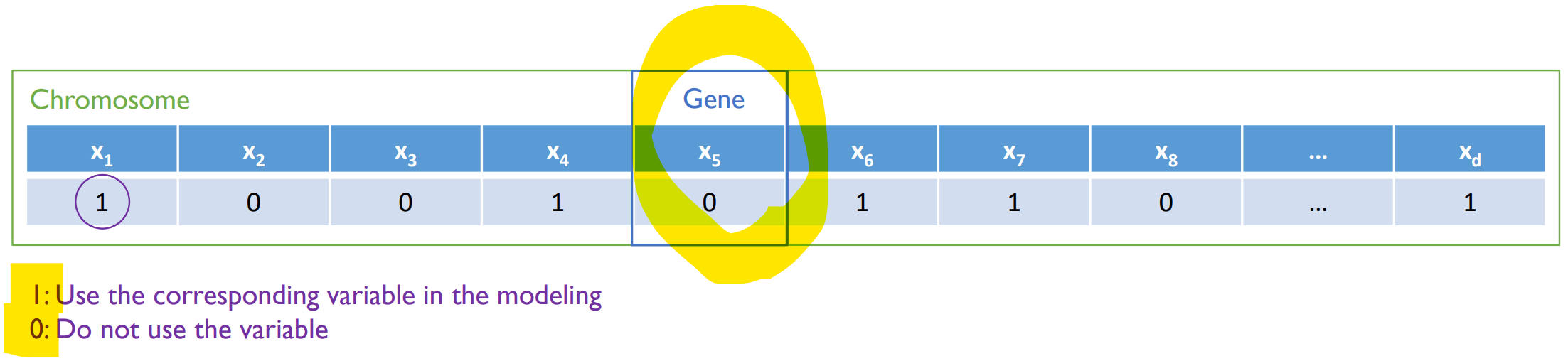
- 1 : 모델링에 사용
- 0 : 모델링에 사용 X
Parameter Initialization
- 염색체의 수 (population) : 100으로 설정한다면, 1세대에서 100개의 변수 부분집합을 평가정한다면, 1세대에서 100개의 변수 부분집합을 평가
- Fitness Function : Chromosome quality 평가
- Crossover Mechanism : 교배 방식
- 돌연변이율
- 종료 조건(Stopping criteria) : 더이상 성능 향상 시킬 필요가 없거나, iteration이 최대치에 도달했을 때 종료
GA Step 2. Fitness Evaluation
어떤 염색체가 더 좋은지 판단하는 기준 (Accuracy처럼 높을 수록 좋음)
- 서로 다른 두 개의 염색체가 같은 fitness value를 가질 경우, feature수가 적은 염색체가 채택
- 서로 다른 두 개의 염색체가 같은 feature 수를 가지는 경우, 높은 성과를 가지는 염색체가 채택
multiple linear regression
- Adjusted R2
- Akaike information criterion (AIC)
- Bayesian information criterion (BIC)
GA Step 3. Selection
Scheme 1 : Ranking (Deterministic selection)
상위 N%의 염색체를 선택(하위 염색체는 선택 X)

Scheme 2 : Proportional to Fitness value
rank를 매기는 것은 모든 염색체가 기여할 수 없기에, 기여도를 통해 결정

Scheme 3 : Roulette Wheel Selection
염색체의 probability를 계산하고, 0~과 1사이의 값으로 변환한 후 룰렛 돌리기
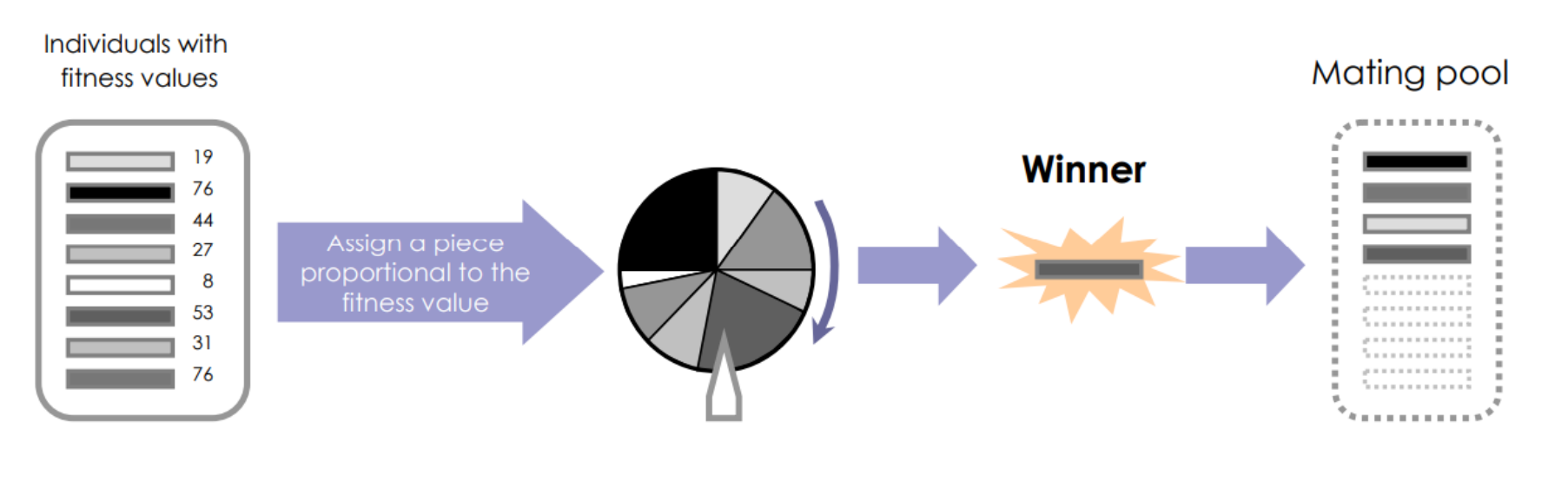
Scheme 4 : Tournament Selection
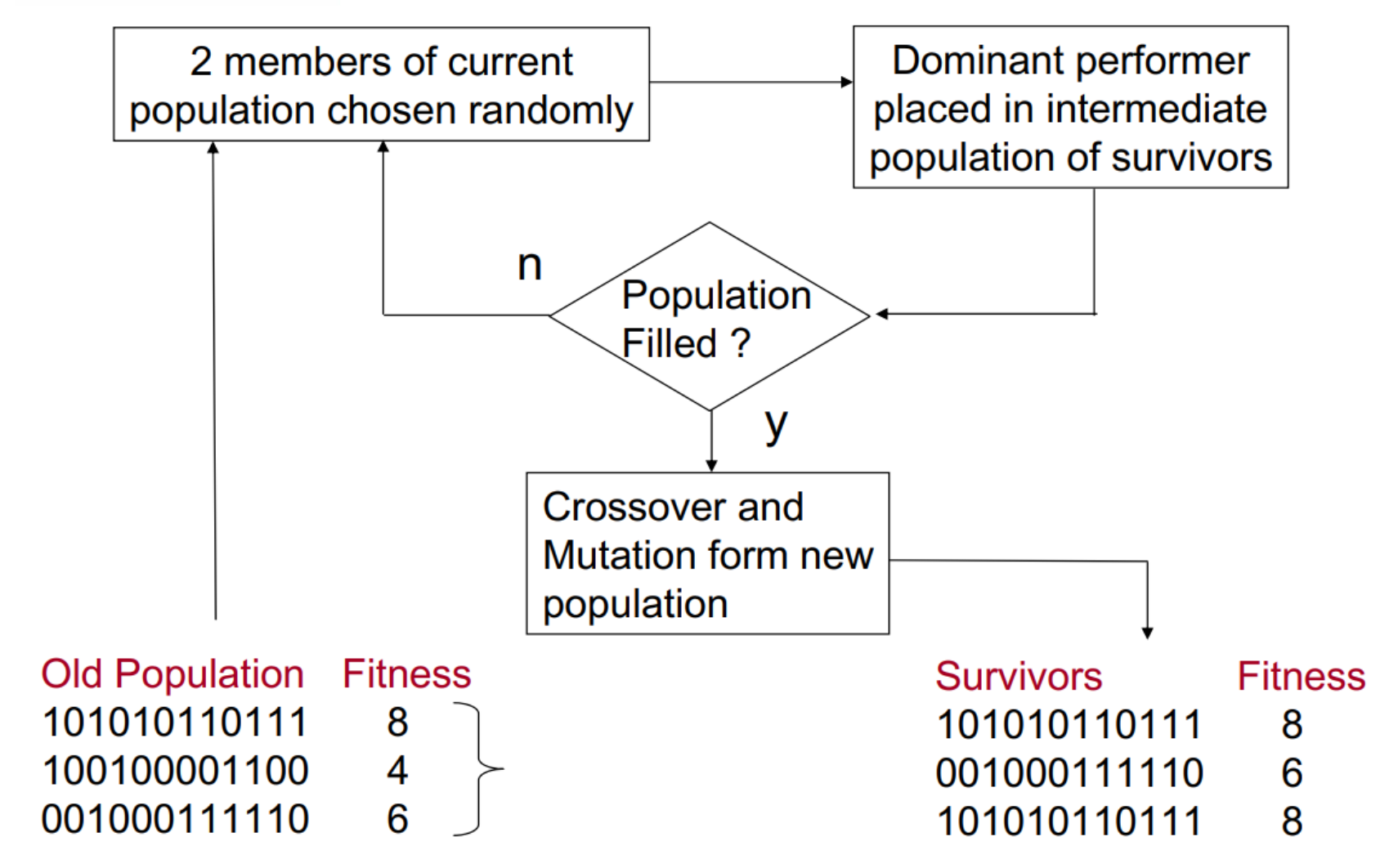
GA Step 4. Crossover
Crossover을 할 때 남성 유전자 44+XY / 여성 유전자 44+XX 에서 child에게 44+(XY/XX)로 전달되는 것에서 착안
2개의 염색체에서 point에 따라 나누고 2개의 Child 염색체를 만듦
Crossover point의 수에 따라 방법이 나뉜다 (Single Point / Multi Point)
Single Point Crossover
2개의 부모 염색체에서 2개의 자식 염색체를 만들기
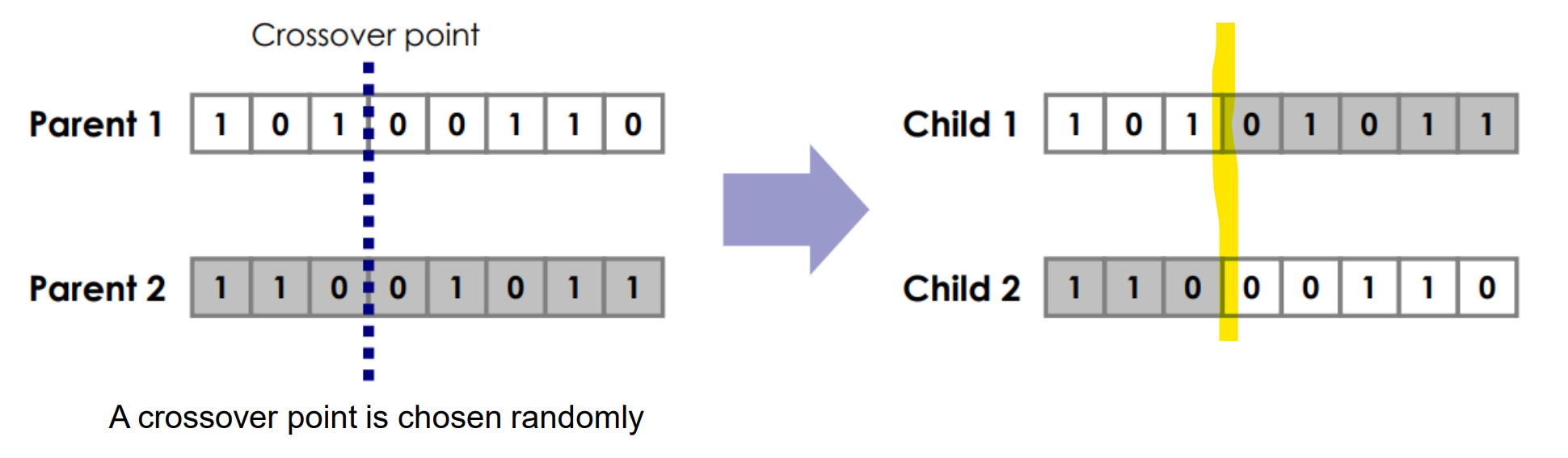
Multi Point Crossover
2개의 부모 염색체에서 2개의 자식 염색체를 만들기

GA Step 5. Mutation
Crossover이 진행될 수록 optima에 수렴하는데, local optima에 빠질 수도 있음
global optima에 수렴되어야 하기에 약간의 변수로 돌연변이 gene을 넣는다.
(local optima에서 빠져나올 수 있는 방법)
- 너무 mutation rate가 크면, 수렴하는데 많은 시간이 소요되기에 굉장히 낮은 값으로 설정해야 함
(ex. mutation rate=0.01)
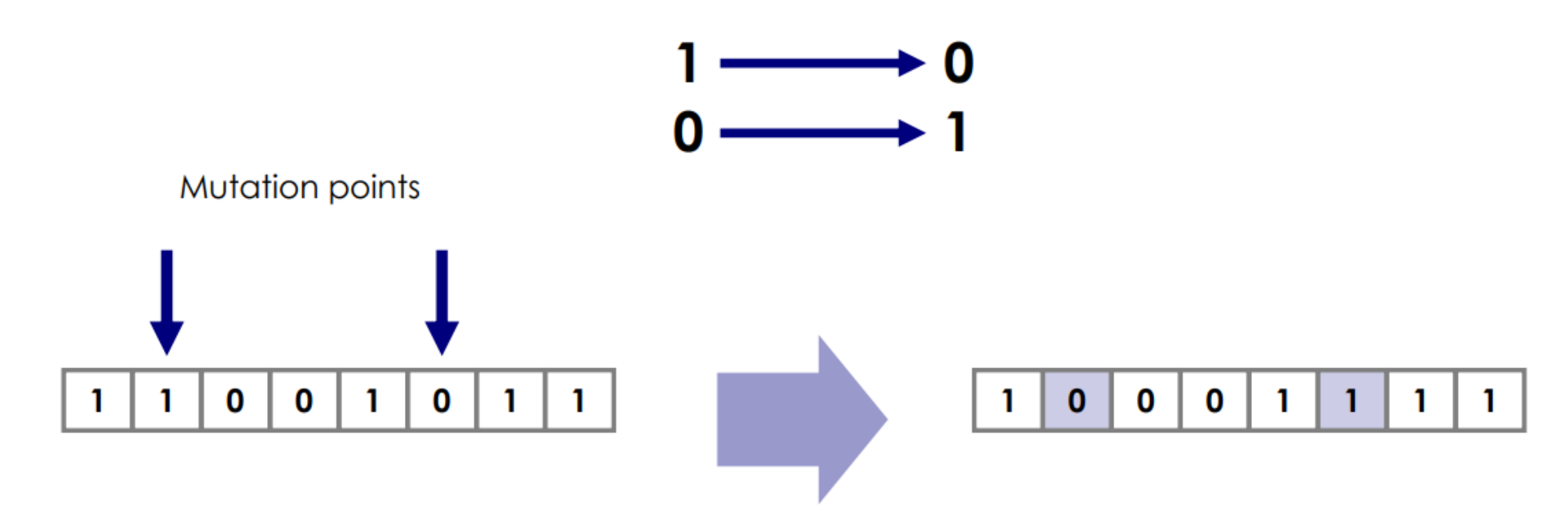
GA Step 6. GA Stopping Criteria
Crossover을 끝나는 시점을 정하기 위한 종료 기준을 정해야 한다.
- Crossover 할 세대 수를 지정(iteration 수를 정하고), 끝나면 종료 (가장 일반적)
- 평균 절대 편차가 임계값 미만일 경우 (유전적 다양성이 작아진 것을 의미)
- 현재 세대에서 다음 세대로의 향상이 거의 없을 경우
3. GA Algorithm 실습 1
: 범위에서 의 최대값
Gene Representation
GA Algorithm을 진행하기 전에, Encoding 해야됨
(binary integer 2진수 사용)
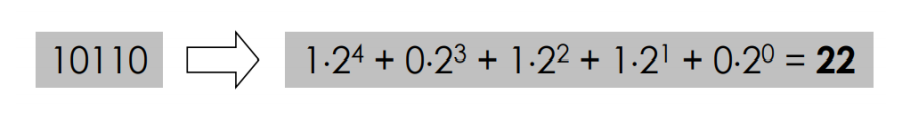
( 0 : 00000~ 31 : 11111)
Step 1. Initialization
첫 세대(generation)은 randomly하게 생성
(population size=4로 가정)
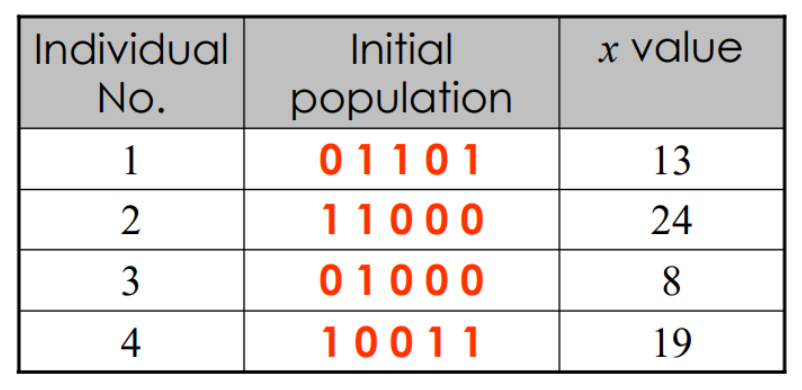
Step 2. Fitness Evaluation
첫 세대를 평가하기 위해 decoding 하여 fitness function value 계산

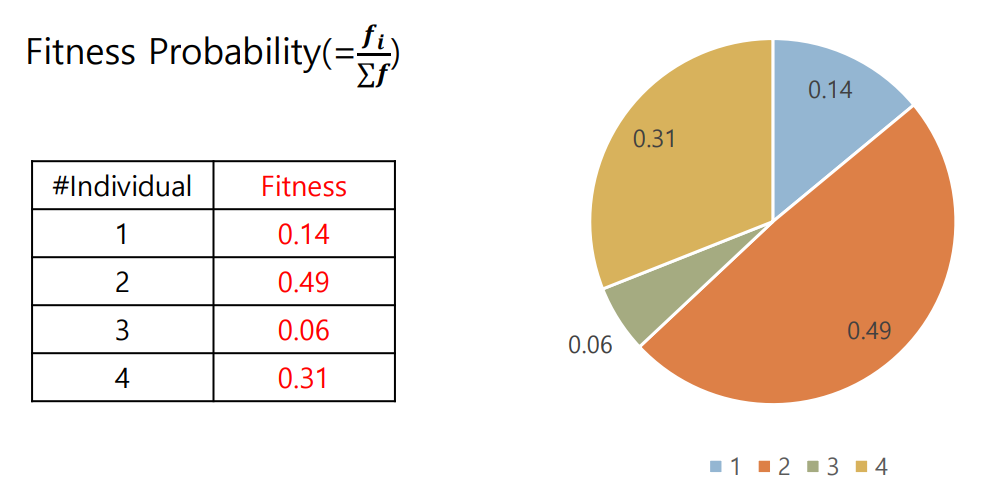
Fitness Probability를 구하기 위하여 값 전체 합에서의 비율을 계산
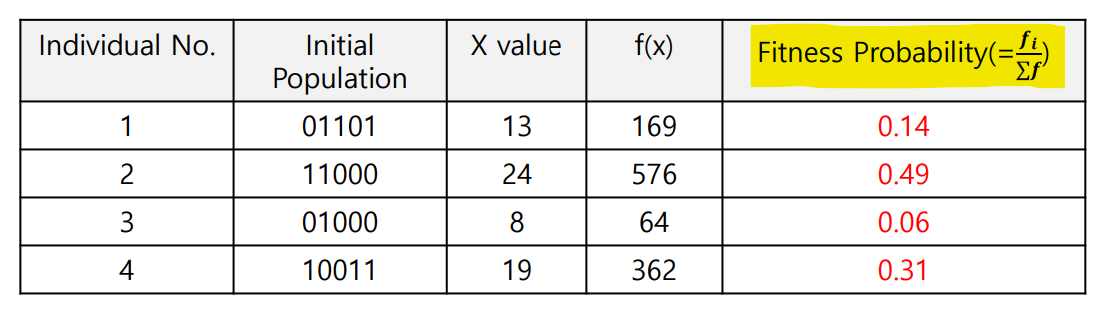
Step 3. Selection
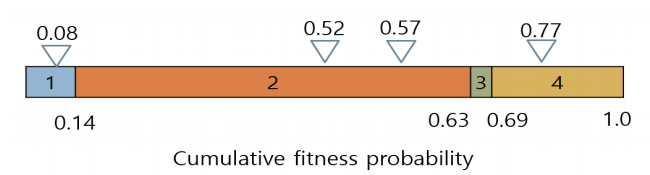
Roulette wheel selection method 를 사용하여 mating pool 선택
Roulette Wheel을 누적합으로 표현한 후, 0~1사이의 값을 4개 randomly하게 추출
그 값에 해당하는 염색체를 mating pool에 작성
(현재 예시 그림에서는 염색체 1, 2, 2, 4가 선택됨)
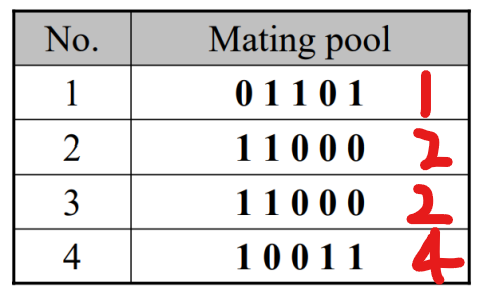
Step 4. Crossover
mating pool에 있는 두 염색체를 randomly하게 선정하여 새로운 염색체 2개를 생성
crossover point 또한 randomly하게 선정됨
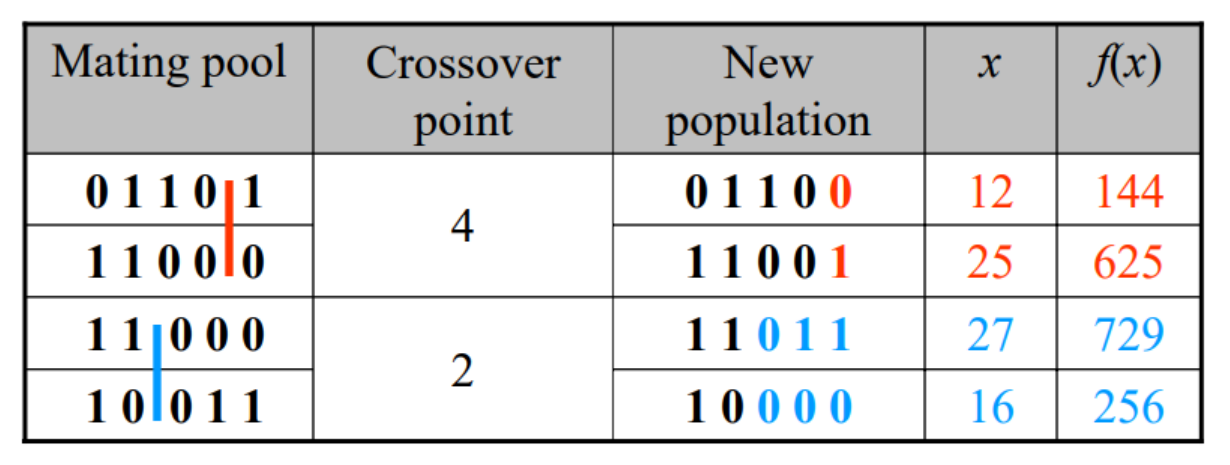
Step 5. Mutation
local minima를 피하기 위해 돌연변이 생성
mutation rate는 굉장히 작은 값이어야 함
(ex. )
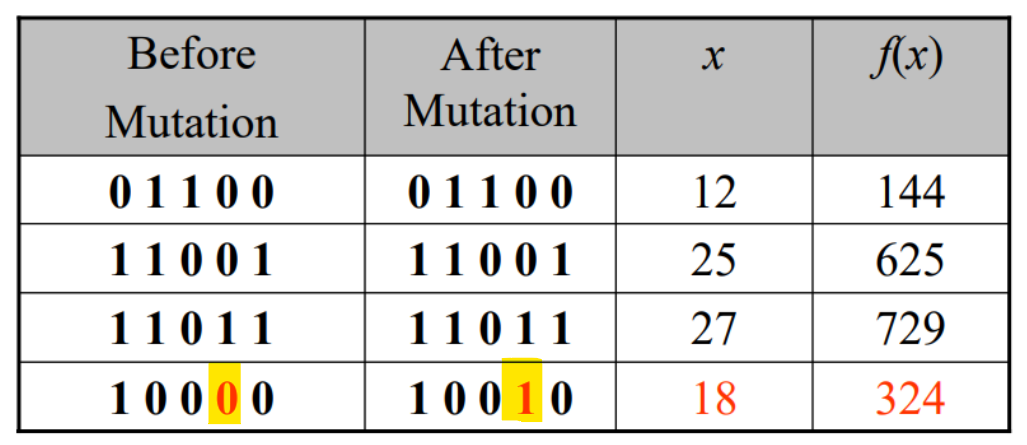
Step 6. Stop Condition
step2~5의 과정을 stop condition이 될 때까지 수행
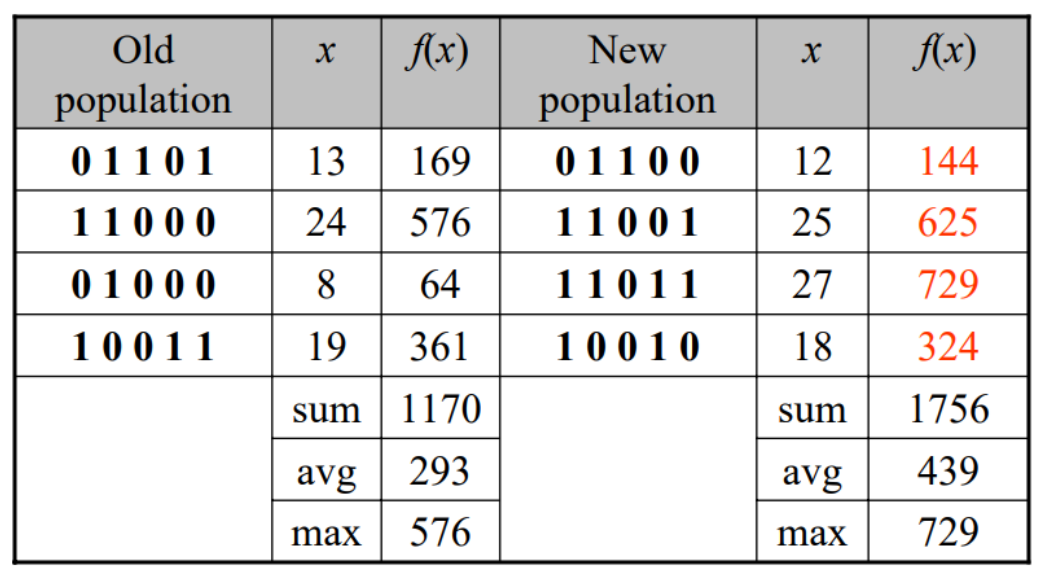
Results
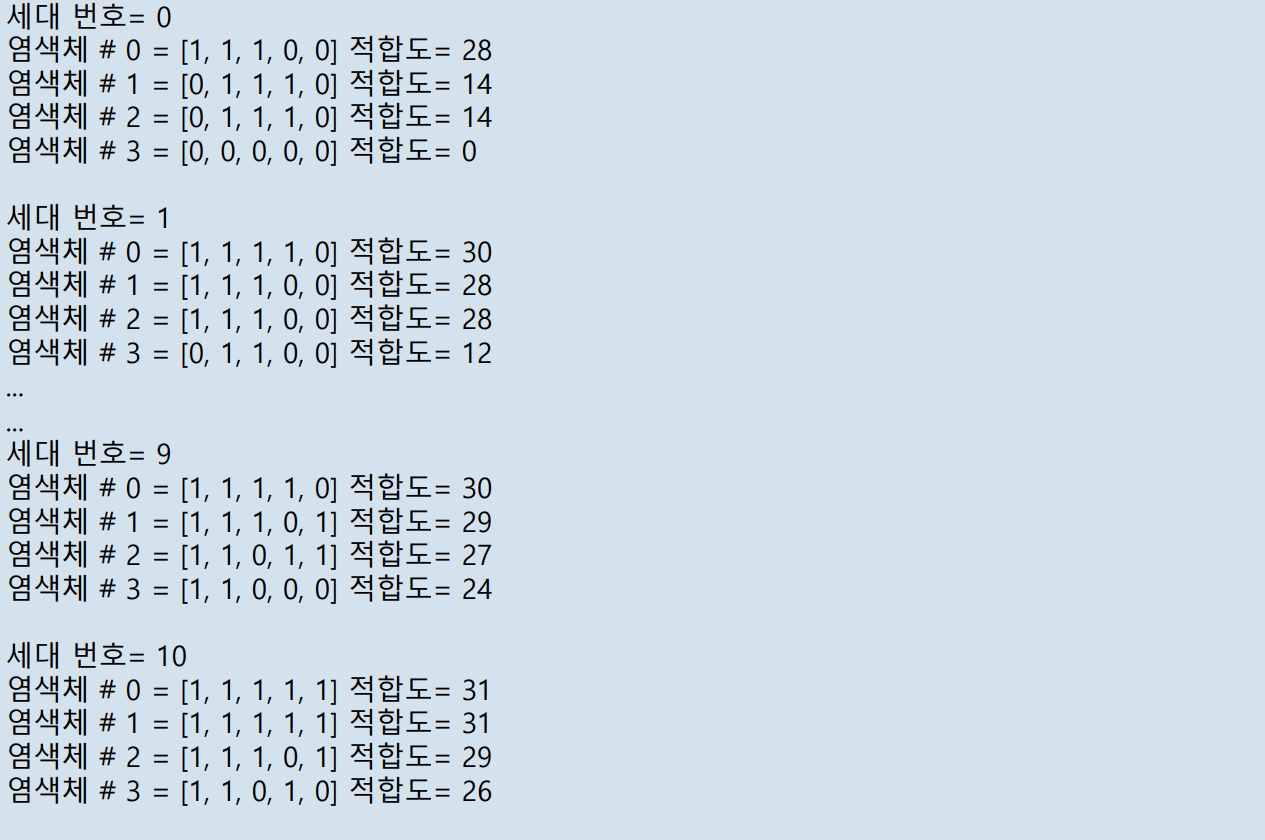
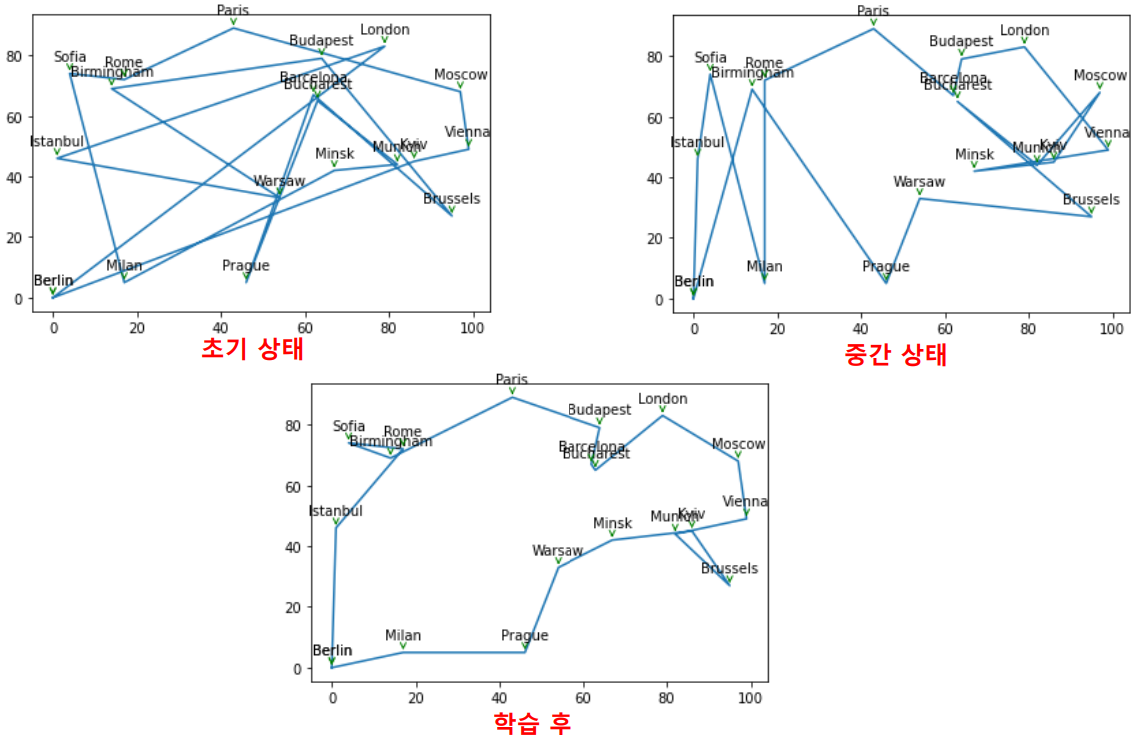
4. GA Algorithm 실습 2
: TSP (Travelling Salesman Problem) 문제
TSP 문제 : 배달원의 최적 경로 탐색
TSP가 어려운 이유
- node가 15만개 있으면 답을 찾기 위해 15!를 계산해야 함
- 현실적으로 정확한 답을 찾기에 어려움
Parameter Setting
parameter setting과 도시 좌표 입력
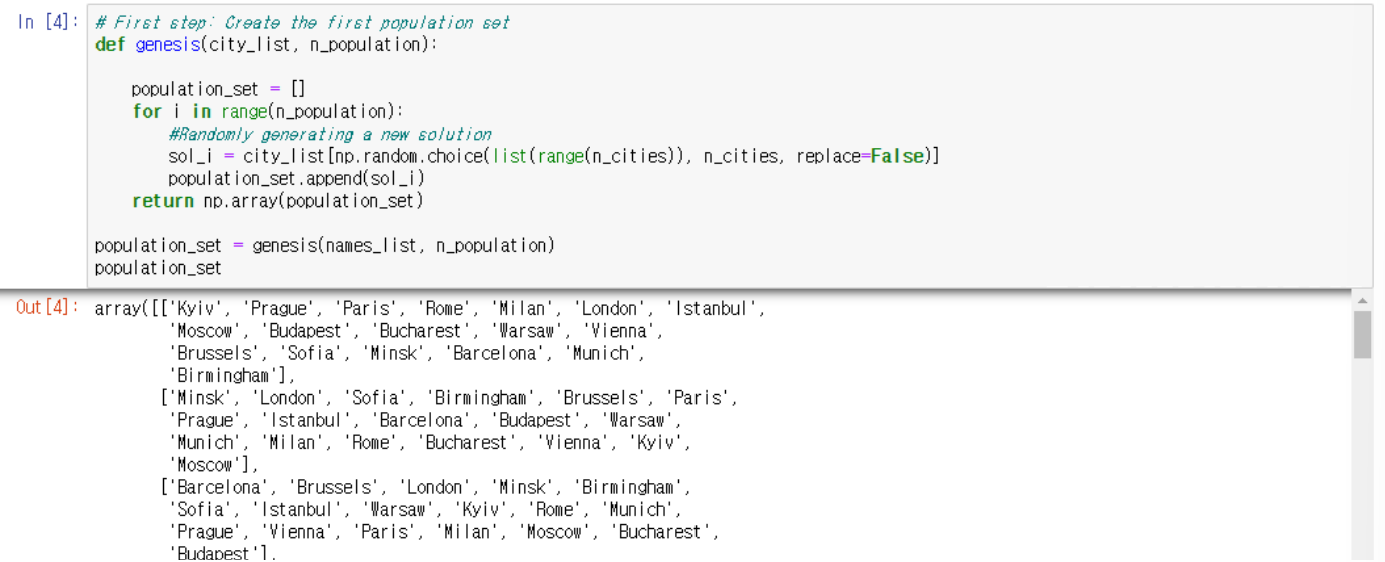
Step 1. Initialization
랜덤으로 도시 경로 설정, Population size 만큼 생성됨
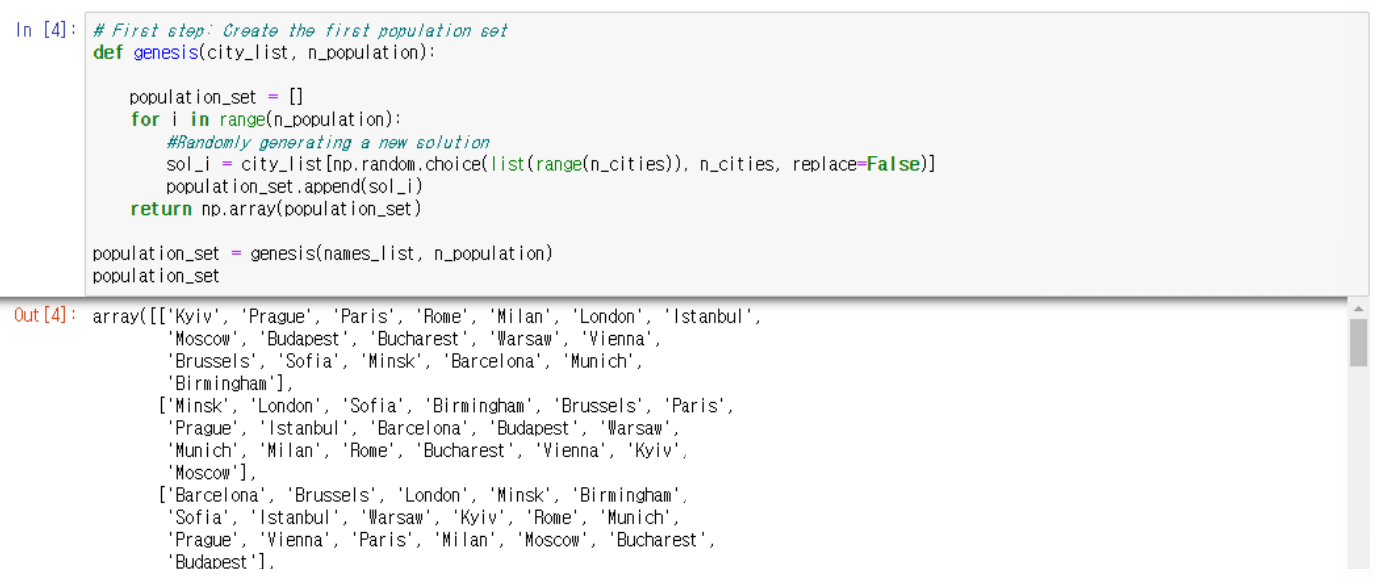
Step 2. Fitness Evaluation
Berlin 에서 시작해서 돌아오는 것이 목표이므로 경로의 처음과 끝에 Berlin 추가
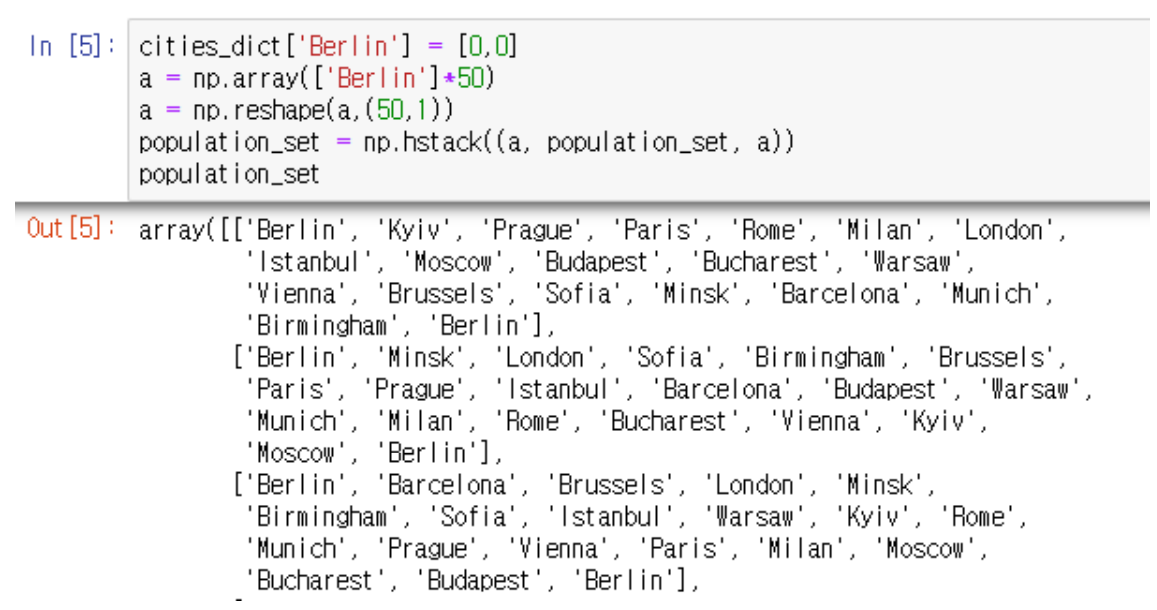
적합도 계산 : 거리 값이 기준이므로 Euclidean distance 적용
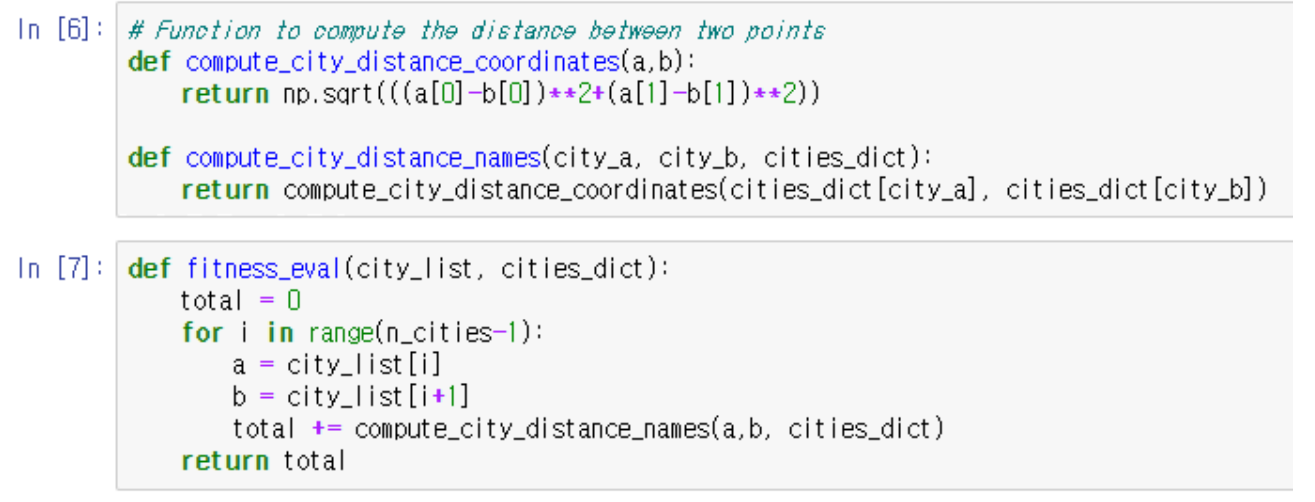
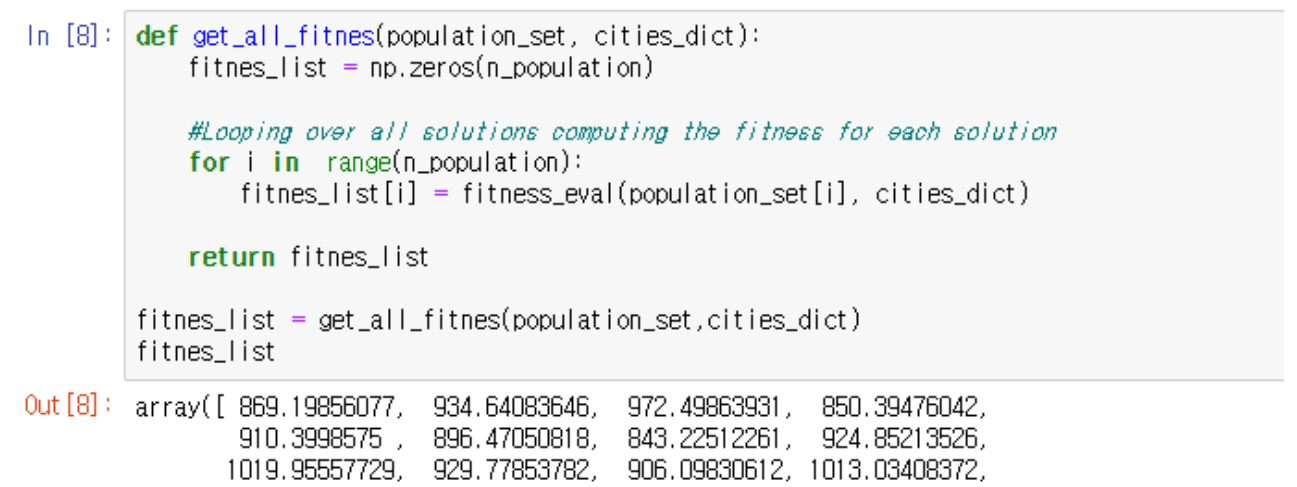
Step 3. Selection
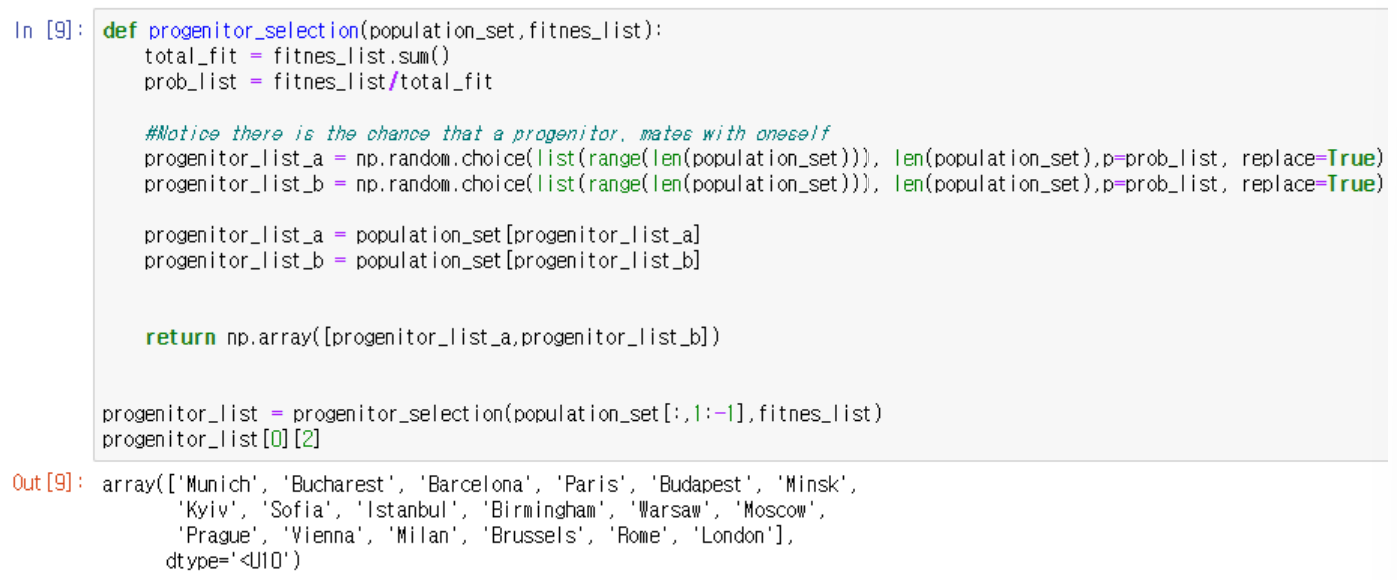
Step 4. Crossover
Selection 과정으로 생성된 a,b에서 a에 5개 도시를 앞에 두고, 나머지 도시를 b에서 순차적으로 합침

Step 5. Mutation
일정 확률로 도시의 순서를 바꿈

Step 6. Stop Condition
Step 2~5.까지의 과정 Stop Condition이 될 때까지 반복

Results