Artificial Intelligence #13 Logistic Regression

분류 문제 : 입력 데이터를 미리 정의된 범주로 나누는 것
(일반적으로 분류 문제는 지도학습 유형으로 다루어짐)

Linear Regression의 한계

• 범주를 구분하는 분류 문제에 취약
• 특이값이나 이상치에 크게 영향 받음
  

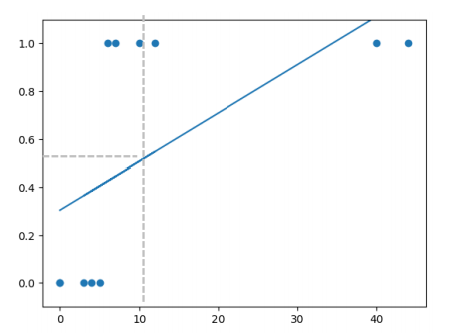
(-> Classification에 Linear Regression을 사용할 수 있으나 정확도가 떨어짐)

1. Logistic Regression

분류 문제에 사용되는 통계적인 회귀 기법
선형회귀와 달리 로지스틱 함수를 사용하며, 결과를 0~1 사이 값으로 제한

• 일반적으로 로지스틱 함수로 시그모이드 함수(Sigmoid Function) 사용

Sigmoid Function

출력이 0~1 사이의 값을 가지며 시그모이드 함수는 S자 곡선의 모양을 가짐(비선형)

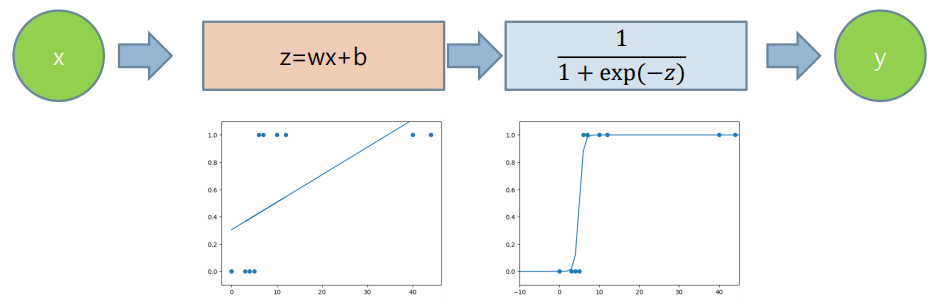
$z=wx+b$의 값을 sigmoid function에 넣음
이때 $w$, $b$ 에 따라 sigmoid function의 특성이 바뀜

가중치 $w$ 변화에 따른 함수 모양

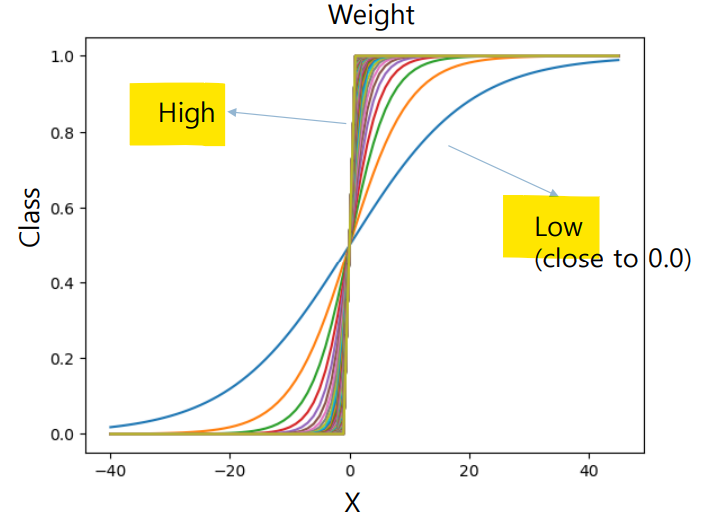
• $w$가 높을 수록 직각에 가까워짐
• $w$가 작을 수록(0에 가까워질 수록) 완만해짐

편향 $b$ 변화에 따른 함수 모양

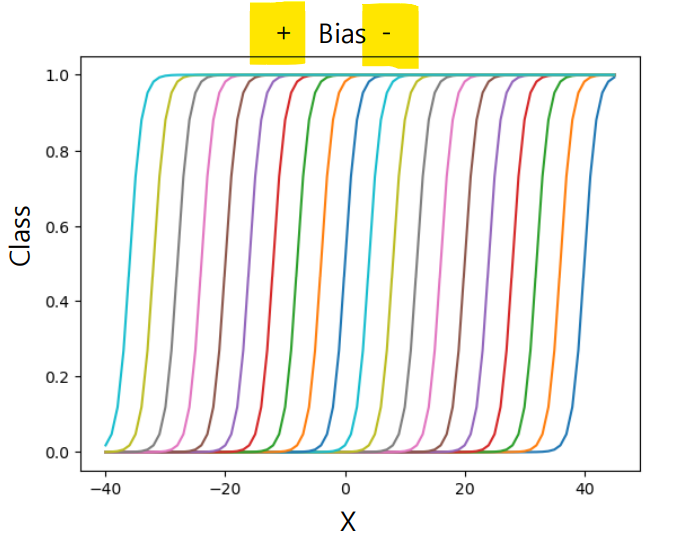
• $b$가 음수로 갈 수록 오른쪽으로 이동
• $b$가 양수로 갈 수록 왼쪽으로 이동

2. Cost Function

Linear Regression의 비용 함수 : MSE loss

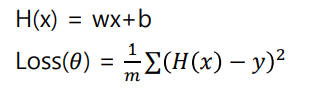
하지만 Logistic Regression에 MSE loss를 적용할 경우, loss function 그래프가 non-convex 상태가 된다.

• Convex 상태일 때는 볼록 함수라서 최적의 값을 찾을 가능성 높음
• Non-convex 상태일 때는 Local minima에 빠질 가능성 높음
  
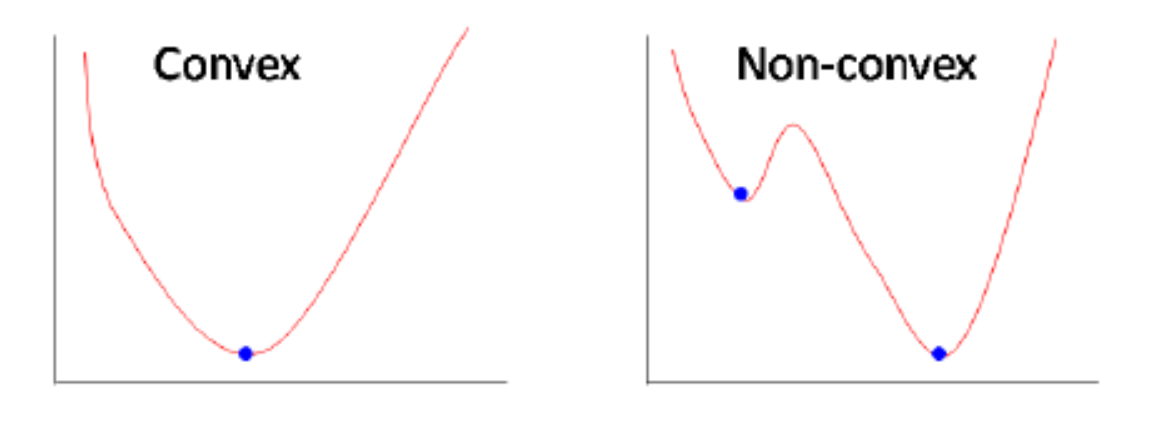
  사진 출처

그래서 로지스틱 회귀에서는 다른 비용함수를 사용한다.

---

Logistic Regression의 비용 함수 : NLL(Negative Likelihood)

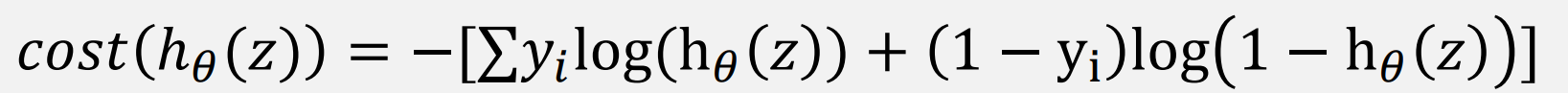
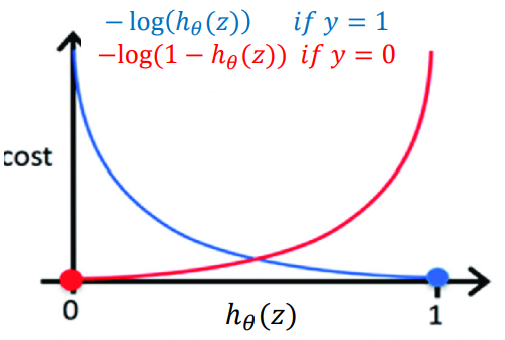
NLL 비용 함수를 사용할 경우, convex 형태의 그래프를 얻을 수 있다.
(-> 경사 하강 가능한 그래프로 바뀜)

3. Gradient Descent

: 미분을 통한 경사 하강을 통해 최적의 파라메터를 찾는 방법

NLL loss의 미분

Loss function 은 $z$에 대한 함수이기에 직접적으로 $w$에 대한 미분 어려움

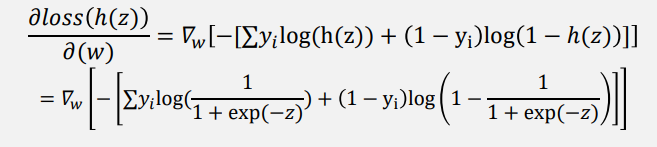
Chain Rule

두 함수를 합성한 합성 함수의 도함수(derivative)에 관한 공식
(마치 사슬이 이어져 있는 것 유사하여 합성함수 미분법을 연쇄법칙이라고도 함)

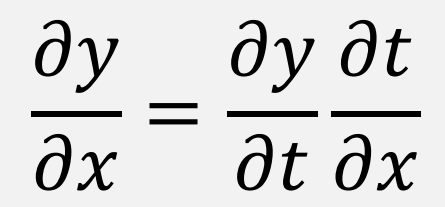
4. Logistic Regression 실습