Artificial Intelligence #14 Multinomial Regression

분류 문제 : 입력 데이터를 미리 정의된 범주로 나누는 것
(일반적으로 분류 문제는 지도학습 유형으로 다루어짐)

Linear Regression의 한계

• 범주를 구분하는 분류 문제에 취약
• 특이값이나 이상치에 크게 영향 받음
  

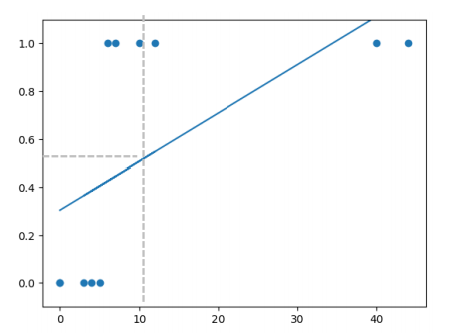
1. Linear Regression의 새로운 한계

분류 데이터는 0,1로 표현되어 데이터의 표현 범위는 $[0.0, 1.0]$
/ Linear Regression의 범위는 $(-∞, +∞)$

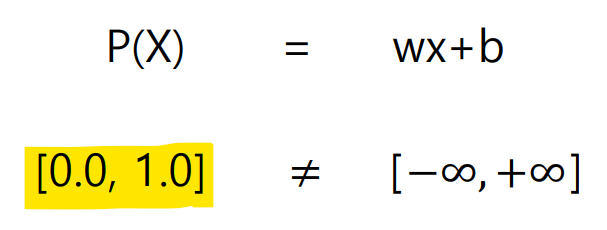
(표현 범위가 서로 달라 식이 성립하지 않는 구간이 존재함)

Odds(승산)

성공/실패 확률로 성공이 실패 확률에 비해 얼마나 더 큰 가를 나타내는 방법

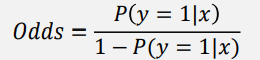
• 성공 확률이 실패 확률보다 커서 비율이 1보다 커질 때 성공 클래스로 분류
• Odds의 표현 범위 : $[0, +∞]$
  

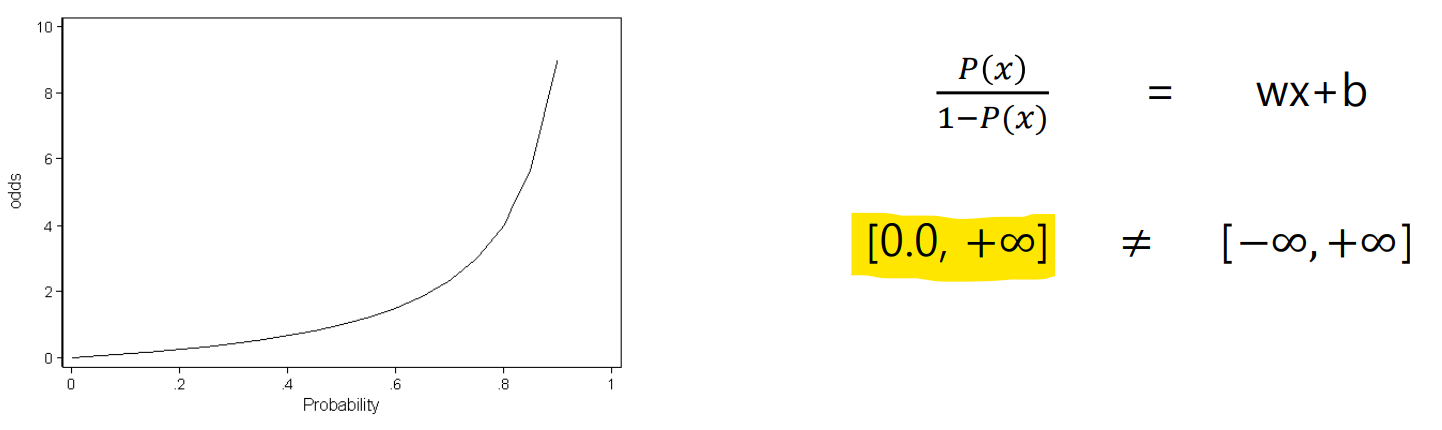
(하지만 여전히 범위가 안 맞는 구간 존재)

Logit(Log Odds)

Odds에 log를 붙여 표현 범위를 $(-∞, +∞)$로 확장

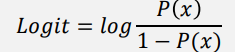
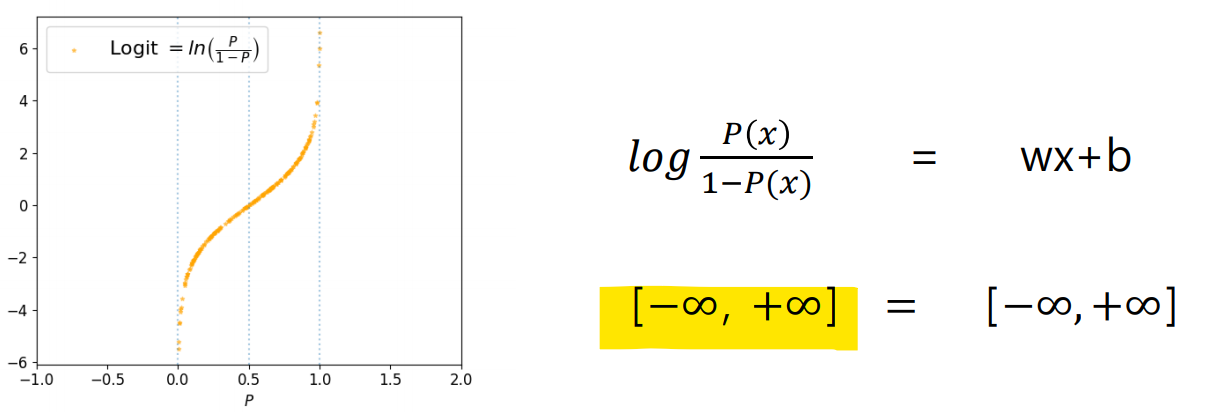
데이터의 표현 범위가 같아져 학습 가능해짐

Sigmoid Function

입력값 $x$를 실수 전체로 받을 수 있지만, $P(x)$ 출력 결과는 항상 0~1 사이 값이 됨

2. Multinomial Classification

분류 문제에서 종속 변수가 3개 이상의 class를 갖는 경우

이 문제를 Logistic Regression으로 풀기 위하여 3가지의 이해 필요

• label 표현 방법 : One-Hot Encoding
• classification 방법 : One vs Rest Classification / Softmax
• model 학습 방법 : Cost Function(Cross Entropy Loss)

label 표현 방법

One-Hot Encoding : 문자나 클래스를 유일한 숫자 벡터로 표현하는 방법

• 단어/클래스를 벡터의 차원으로 만든 후, 표현하고 싶은 단어의 인덱스에 1/나머지는 0 부여
  

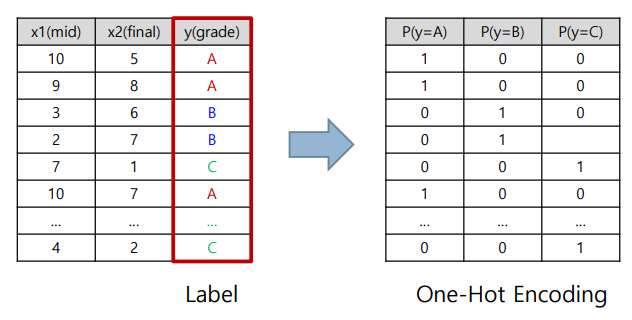
classification 방법

One vs Rest Classification
: One-Hot Encoding에 대응하는 각각의 독립적인 모델을 만들고 학습한 후, 새로운 입력에 대해 가장 확률이 높은 결과를 선택하여 분류하는 방법

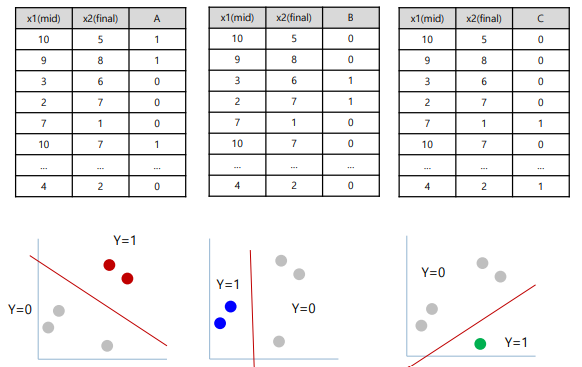
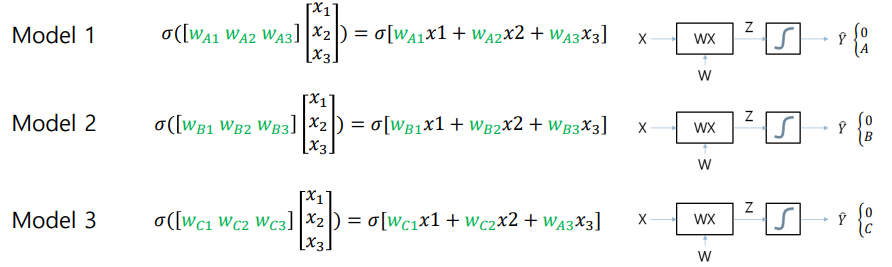
Softmax
: 다중 클래스 분류 문제에서 출력으로 사용되는 함수
(-> 상대적 중요도를 고려하여 확률로 변환하는 함수)

위의 사진을 통해 sigmoid 함수와 softmax 함수의 출력 차이를 확인할 수 있음
(다중 분류에는 softmax 함수가 적합)

model 학습 방법

Cross Entropy Loss (Cost Function)

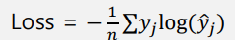
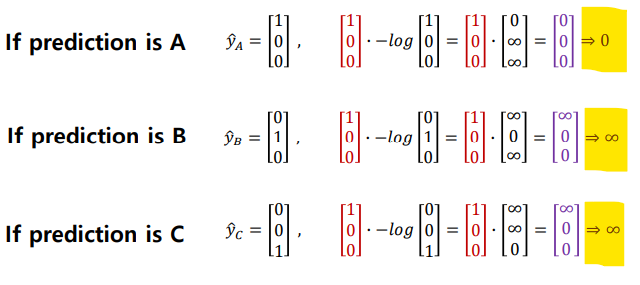
• prediction이 정확할 경우 : loss=0
• prediction이 부정확할 경우 : loss 기하급수적으로 증가

NLL(Negative Log Likelihood) 와 Cross Entropy의 관계

NLL(Negative Log Likelihood) : 이진 분류, sigmoid 함수 사용할 때
Cross Entropy : 다중 분류, softmax 함수 사용할 때

Gradient Descent