Artificial Intelligence #03 Bayesian Inference

전문가 시스템의 문제점 Artificial Intelligence #01 Expert System

• 데이터의 불확실성 : 측정 오류나 오차
• 지식의 불완전성 / 전문가들의 관점이 다른 경우 / 정보 획득의 불완전성
• 부정확한 언어

1. 확률의 종류 (빈도론적/베이지안)

빈도론 : 반복적인 사건의 빈도

동일한 시행을 무한 반복했을 때 관심있는 사건의 발생 빈도
(ex. 동전 던지기, 주사위 던지기, 카드 뽑기)

$(확률) = (관심있는 사건 발생횟수)/(전체 시행 횟수)$

빈도론 확률의 한계 : 실제로는 무한 반복이 불가능, 확률계산의 결과가 불확실!

베이지안 : 확률을 '주장에 대한 신뢰도'로 해석

믿음의 정도로 사건의 발생 확률 신뢰도를 추론
(ex. 내일 비가 올 확률 30%)

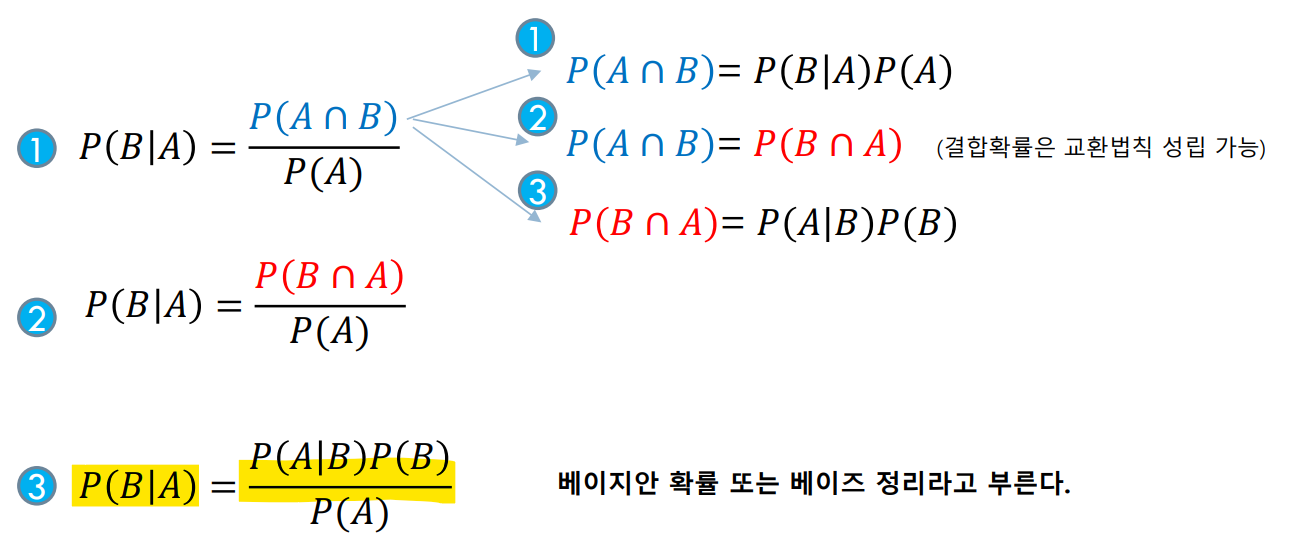
2. 베이즈 정리 (Bayes' Theorem)

베이즈 정리 유도

$𝑃(𝐵|𝐴) =𝑃(𝐴∩𝐵)/𝑃(𝐴)$ (조건부 확률 수식)
$𝑃(𝐵|𝐴) =𝑃(𝐴|B)P(B)/𝑃(𝐴)$ (베이즈 정리 수식)
조건부 확률을 통해 베이즈 정리 수식을 유도할 수 있음

베이즈 정리의 해석

실제로는 문제에서 사전확률, 우도확률을 구하기 쉽기에 이것으로 사후 확률을 구할 수 있다는 것이 의미가 있다.
(사전확률을 바탕으로 사후확률을 update)
그리고 빈도론 확률의 문제점(무한대로 계산)을 극복할 수 있다.

• 증거와 가설이 1개일 경우
  증거와 가설이 한 개이기에 $P(E)$는 집합과 그의 여집합으로 이루어진다.
  

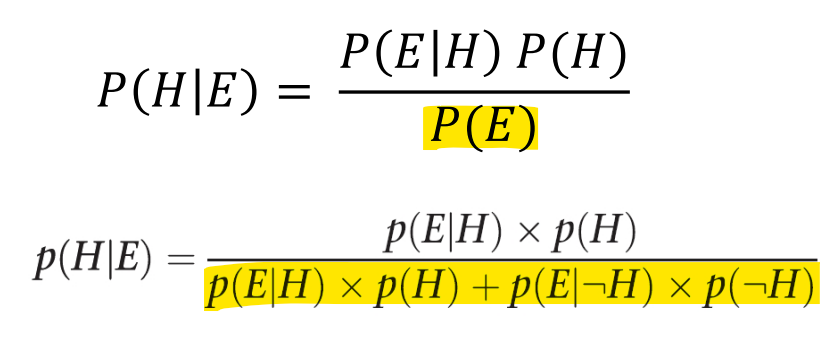
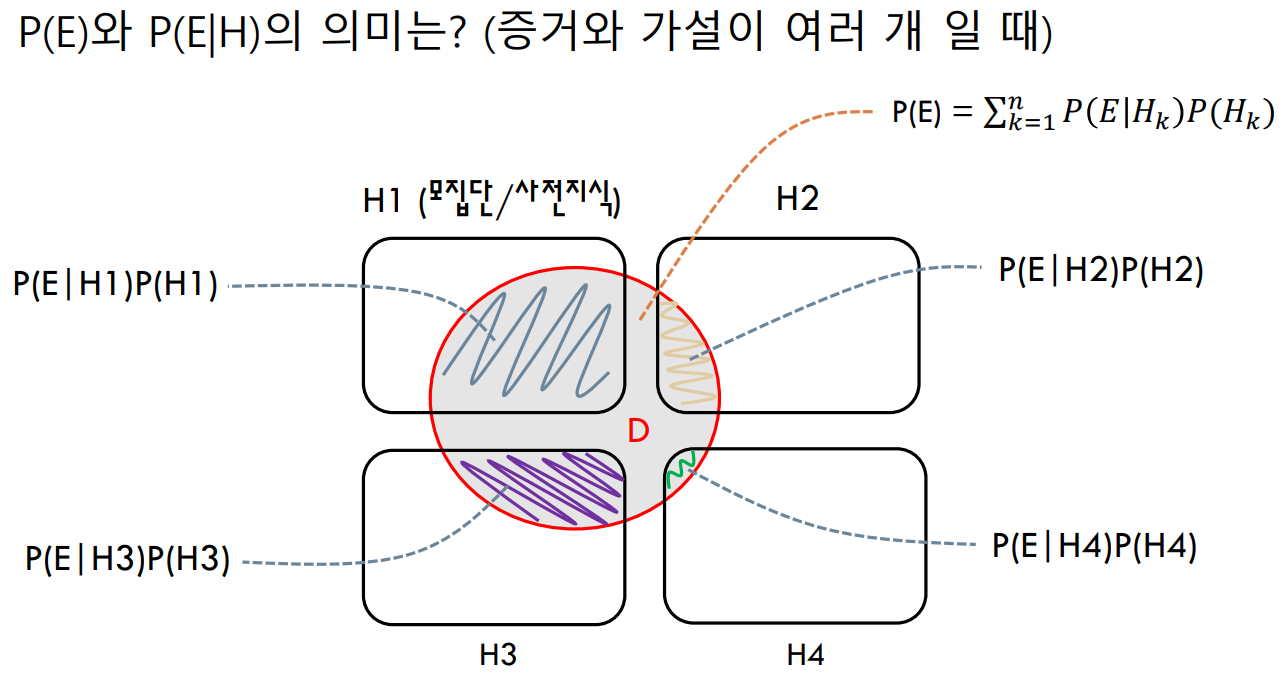
• 증거와 가설이 여러 개일 경우
  위 경우와 달리 $P(E)$는 여러 증거와 가설로 이루어진다.
  

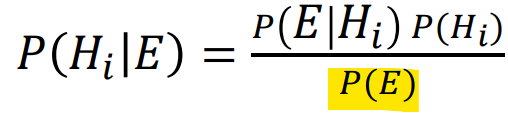
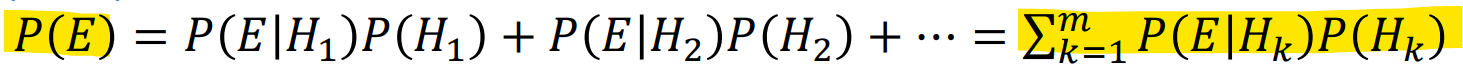
3. 베이즈 정리 예제

[ 예제 1 ]

[ 예제 2 ]

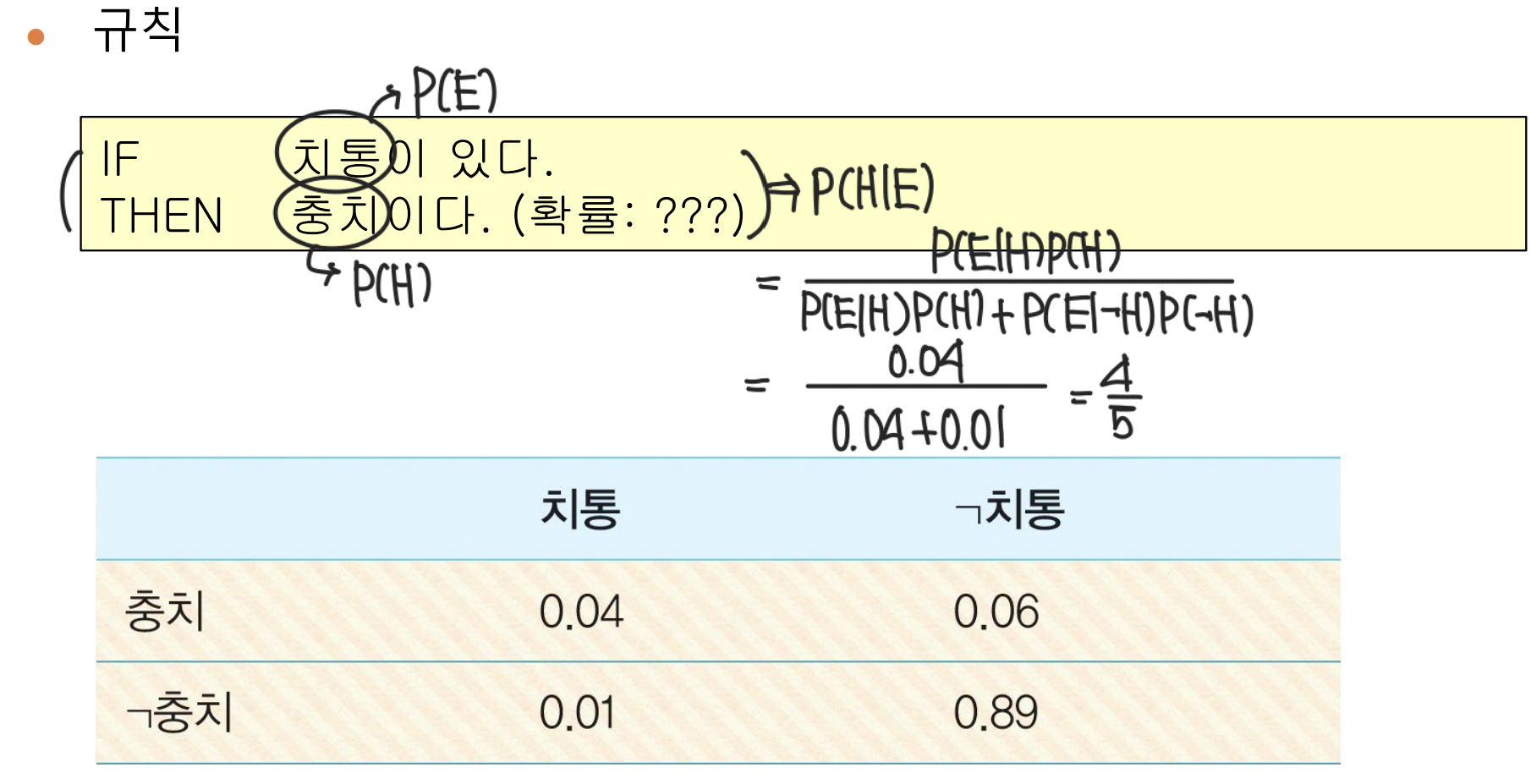
[ 예제 3 ]

[ 예제 4 ]

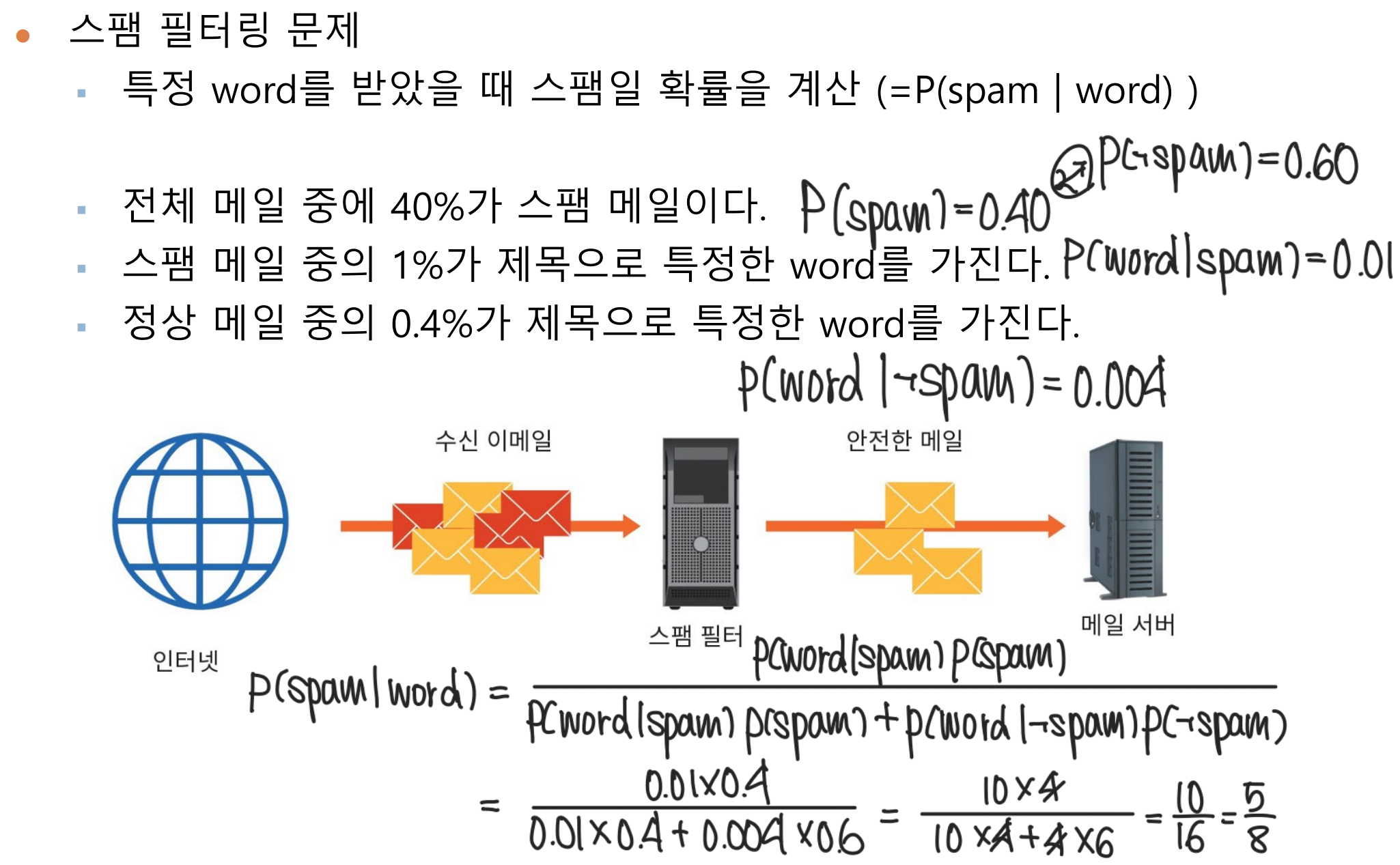
[ 예제 5 ]

4. 베이즈 정리 실습 1

붓꽃 분류문제를 Gaussian Naive Bayes Model로 풀어보기

붓꽃 데이터 확인

data shape 및 data feature과 class target 확인

from sklearn.datasets import load_iris

#데이터 로드
iris=load_iris()
print(iris)
print(iris.feature_names)
print(iris.target_names)


#data와 target으로 분할
data=iris['data']
target=iris['target']

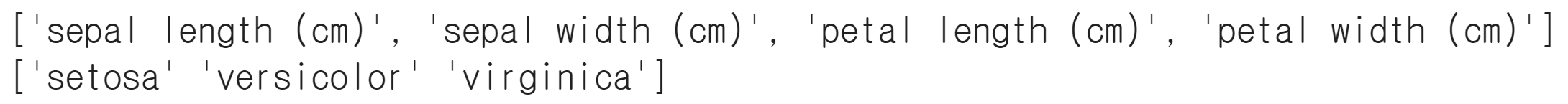
data shape (1,4) 으로 data마다 특성이 4개(꽃받침 길이/꽃받침 너비/꽃잎 길이/꽃잎 너비) 포함되어있다. target의 class는 3개이며, class 0은 ‘setosa’ class1은 ‘versicolor’ class2은 ‘virginica’ 이다.

붓꽃 데이터 특성의 평균, 분산

#class별로 평균, 분산 구하기

means = {}
variances = {}

for i in range(3):
    target_data = data[target==i]
    means[i] = target_data.mean(axis=0)  #열의 평균을 계산해야되기에 axis=0으로 설정
    variances[i] = target_data.var(axis=0)

print("평균")
for k,v in means.items():
    print(f"Class {k}: {v}")

print("분산")
for k, v in variances.items():
    print(f"Class {k}: {v}")

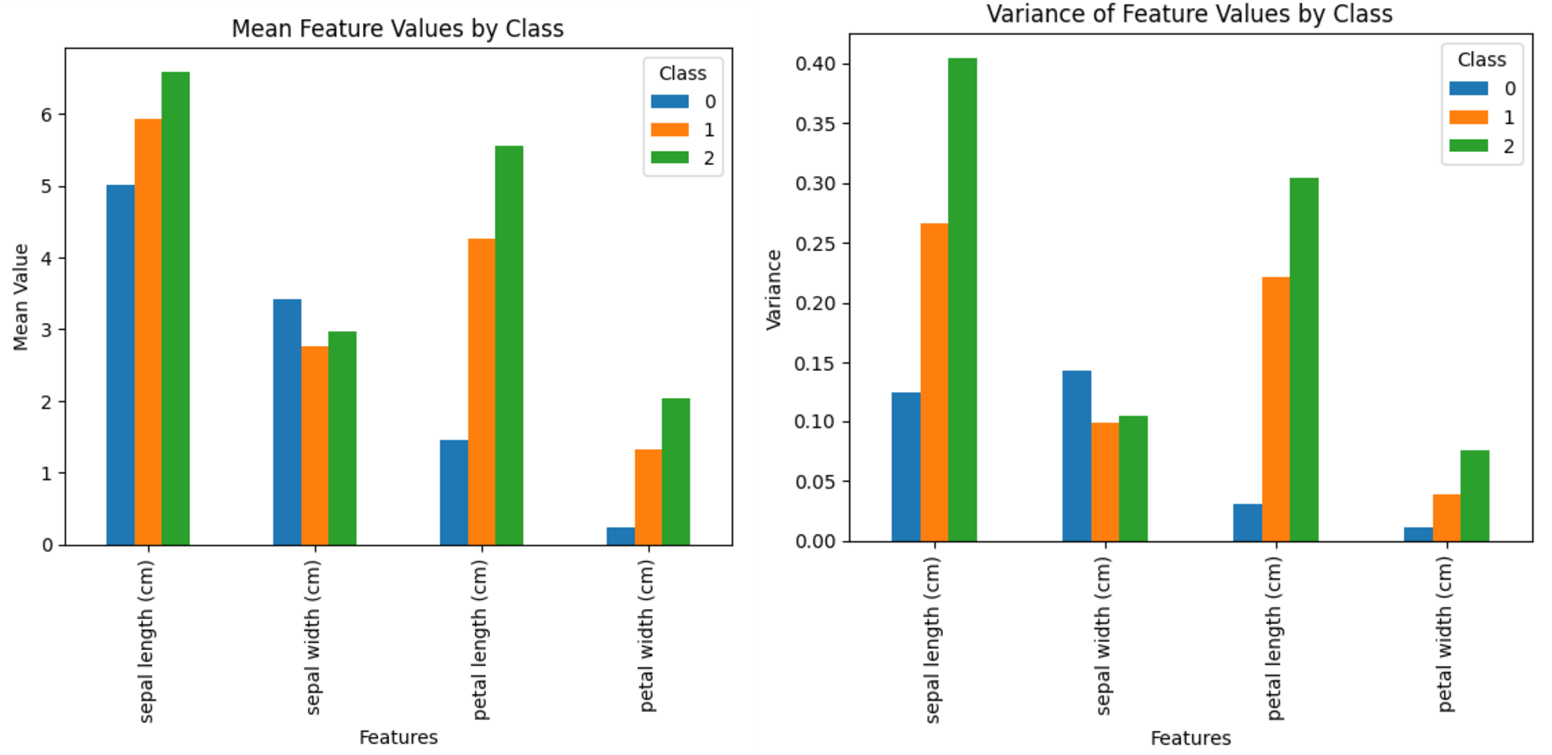
특성 1(꽃받침의 너비)만을 보았을 때, 만약 새 데이터의 특성1이 5.0이라면

class 0 : 평균 5.006으로 다른 class 1, 2에 비해 평균 오차가 가장 적으며, 분산도 제일 적기에 새 데이터는 class1에 속할 확률이 높을 것이다.
class 1 : 평균 5.936으로 class 0에 비해 오차가 더 있으며, 분산도 class 0에 비해 낮더라도 새 데이터는 class 0에 비해 class1에 속할 확률이 낮을 것이다.
class 2 : 평균 6.588으로 다른 class 0, 1에 비해 평균 오차가 가장 높기에, 분산이 크더라도 class2에 속할 확률은 매우 낮을 것이다.

각각의 평균과 분산으로 어느 class에 속할 확률이 높은지 해석할 수 있다.

붓꽃 데이터 모델 학습 및 평가

from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

X_train, X_test, y_train, y_test = train_test_split(data, target, test_size=0.2, random_state=42)
model = GaussianNB()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)

# 정확도 평가
accuracy = accuracy_score(y_test, y_pred)
print(f'정확도: {accuracy:.2f}')

from sklearn.metrics import classification_report

report=classification_report(y_test, y_pred)
print(report)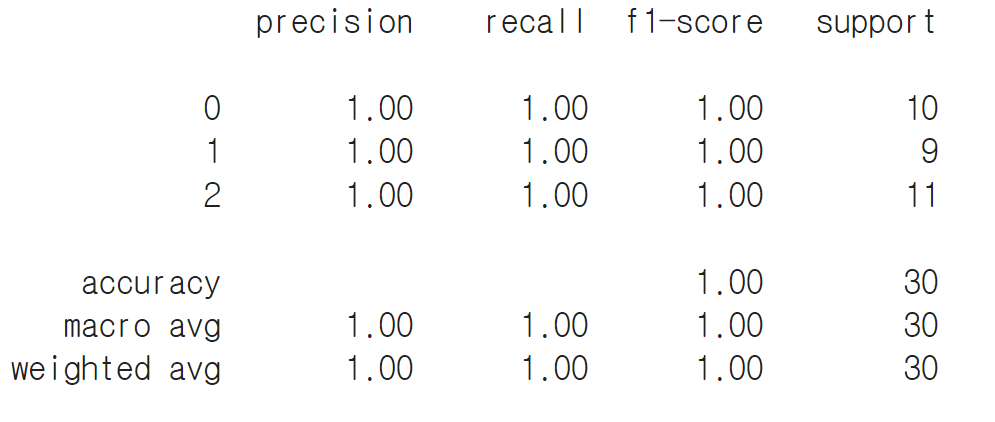

Gaussian Naive Bayes 작동 원리

특성의 평균과 분산이 그 클래스 내에 어떻게 분포되어 있는지, 그리고 그 분포에 따라 새 데이터가 해당 클래스에 속할 가능성이 얼마나 되는지를 결정하는 핵심 요소로 작용하며, 이에 대한 계산이 베이지안 확률로 이루어져 있다.

5. 베이즈 정리 실습 2

: 베이지안 추론 기반의 스팸 필터링 프로그램 개발

스팸/정상에 대한 데이터

스팸 메일이 6개에 26단어이고, 정상 메일이 7개에 29단어인 것을 확인할 수 있다.

스팸 정상에 대한 사전 지식

위의 데이터에서 전체 메일의 개수 중 어떤 것의 메일의 수로 사전 지식을 구성해야 된다.

$P(spam) = 6/(6+7)$
$P(ham) = 7/(6+7)$

추론 모델의 목표

새로운 메일을 받았을 때 spam인지 ham인지 메일 유형을 분류해야 한다.

$argmax[P(spam|text), P(ham|text)]$

$P(spam|text)=(P(text|spam)*P(spam))/P(text)$
$P(ham|text)=(P(text|ham)*P(ham))/P(text)$

(이때 $P(text)$는 $argmax$식 안에 공통으로 있으므로 대소 관계 비교할 때 크게 신경쓰지 않아도 된다.)

$P(spam|text)=P(text|spam)*P(spam)$
$P(ham|text)=P(text|ham)*P(ham)$

-> 이 식으로 계산하여 $argmax$를 판단해도 된다.

Example : "you lottery"

$P(spam|text)=P(you|spam)*P(lottery|spam)*P(spam)=(1/26)*(1/26)*(6/13)$
$P(ham|text)=P(you|ham)*P(lottery|ham)*P(ham)=(0/26)*(0/26)*(7/13)$

지금의 ham 예시처럼 베이지안 추론 시 한 번도 등장하지 않은 사건에 대해서, 추론 결과는 항상 0이다
(제로 확률(Zero Probability) 문제 있음)

---

Laplace Smoothing

1. 각 이벤트의 분자에 𝛼 (𝛼> 0) 를 더해 줌 (default:1)
2. 분모에 k를 더해 줌 (K: 이벤트 종류 수)
   

Example : "you ticket lottery"

sol 1. Bayesian Inference

$P(spam|text)=P(you|spam)*P(ticket|spam)*P(lottery|spam)*P(spam)$
$=(1/26)*(0/26)*(1/26)*(6/13)=0$
(기존 방식으로는 'ticket'이라는 새로운 word로 인해 0으로 계산됨)

sol 2. Bayesian Inference with Laplace Smoothing

$a=1, k=2$ (spam/ham - 2개의 class)

$P(spam|text)=P(you|spam)*P(ticket|spam)*P(lottery|spam)*P(spam)$
$=(1+1/26+2)*(0+1/26+2)*(1+1/26+2)*(6/13)$
(Laplace Smoothing을 통해 최소한 확률이 0이되는 경우를 막을 수 있음)