1. Binary Classification Evaluation
: 이진 분류에서 사용되는 평가 지표
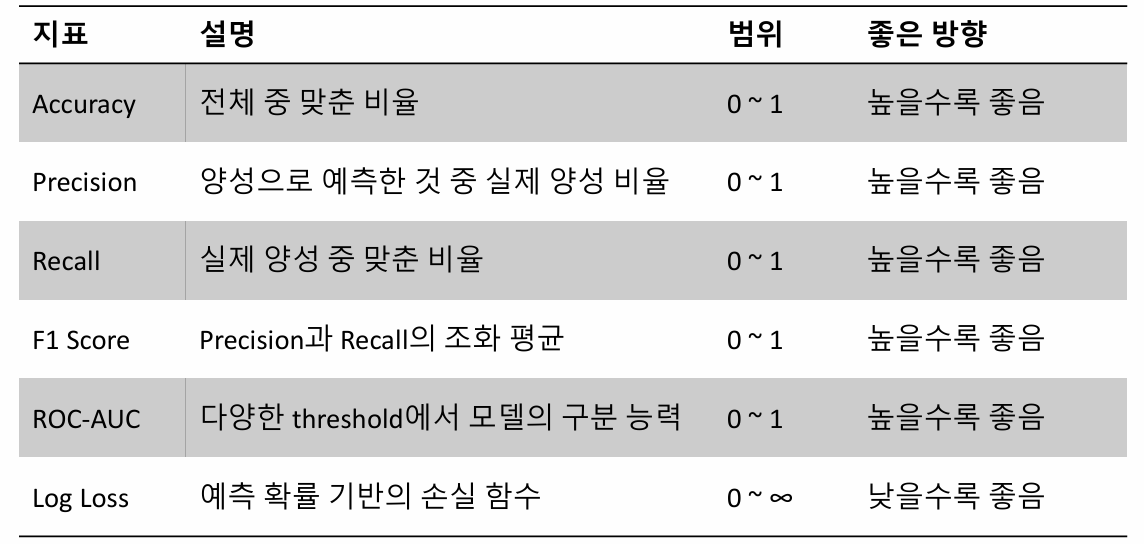
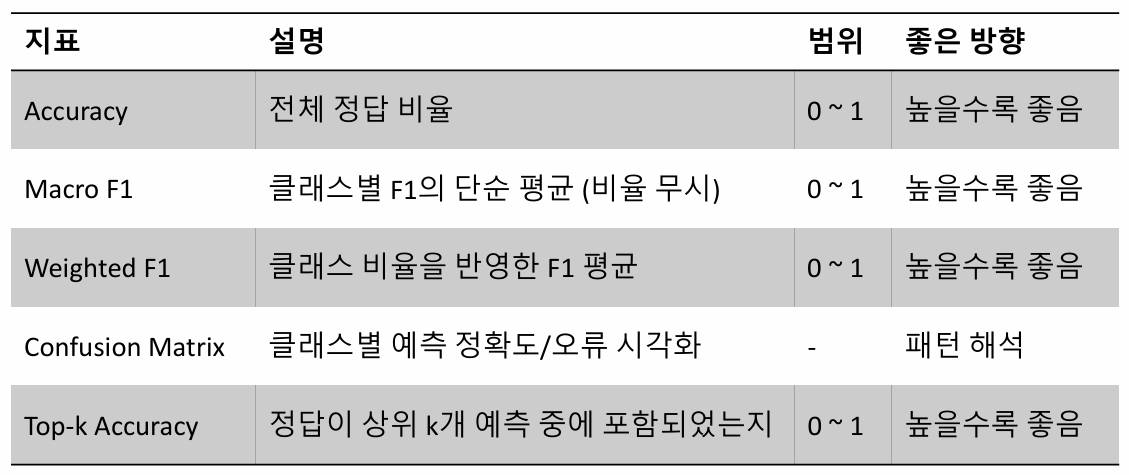
Accuracy (정확도)
전체 예측 중에서 모델이 정확하게 맞춘 비율
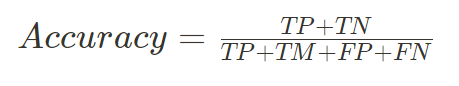
단점
- class 불균형에 민감
: 95%가 class가 같을 경우, 같은 class만 예측해도 95% 정확도 - 오류의 중요도를 반영하지 못함 : FN과 FP가 중요할 때 부적합
(틀리면 치명적인 문제가 발생하는 상황인 경우)
Precision (정밀도)
model이 Positive라고 예측한 결과 중 실제로 Positive인 비율
(Positive의 판단을 얼마나 신뢰할 수 있는가)
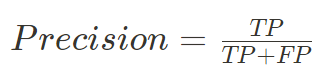
Precision이 중요한 경우
: 오탐의 위험이 큰 상황
(위협이 아닌 것을 위협으로 간주하는 경고가 치명적일 경우)
- 스팸 필터링 : 정상 메일을 스팸으로 판단하면, 중요한 정보를 놓칠 수 있음
- 암 진단 : 암이 아닌데 암으로 진단할 경우 불필요한 비용 발생
- 제조 현상 : 시스템 이상이 없는데 이상으로 판정할 경우 재가동 비용 발생
단점
- FN의 경우를 고려하지 않음
Recall (재현율)
model이 실제 Positive인 클래스 중 정확하게 Positive로 분류한 비율
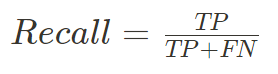
Recall이 중요한 경우
: 중요한 사건이나 질병, 위험 요소 등을 놓치지 않고 모두 찾아야 할 때 중요
- 의료 진단 시스템
- 금융 사기 탐지
- 재난 예측 및 경고
단점
- FP의 경우를 고려하지 않음
F1-Score (조화평균)
Precision (정밀도), Recall (재현율)을 하나로 통합하여 균형 잡힌 평가를 제공하는 지표
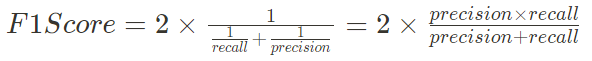
F1-Score의 특징
- 두 개가 불균형을 이루면 낮은 값을 보임 / 두 지표가 균형을 이루면 높은 점수를 받게됨
- class 불균형이 심한 data set에 유용
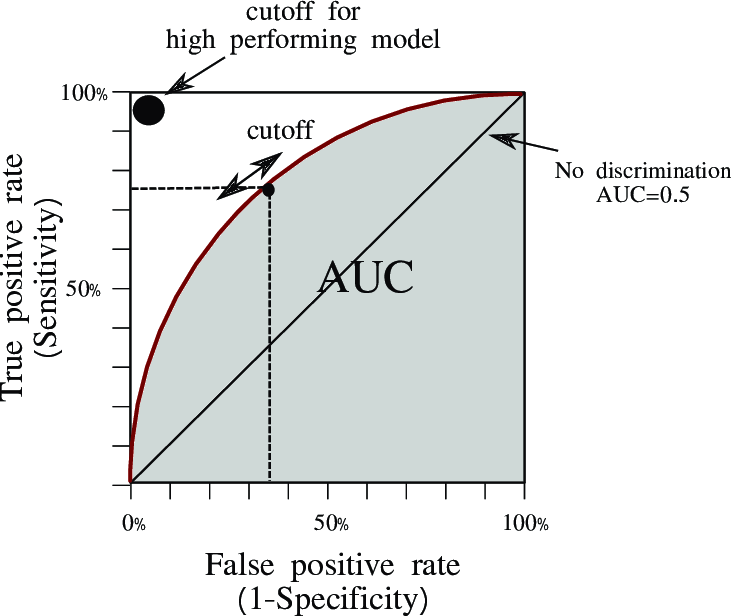
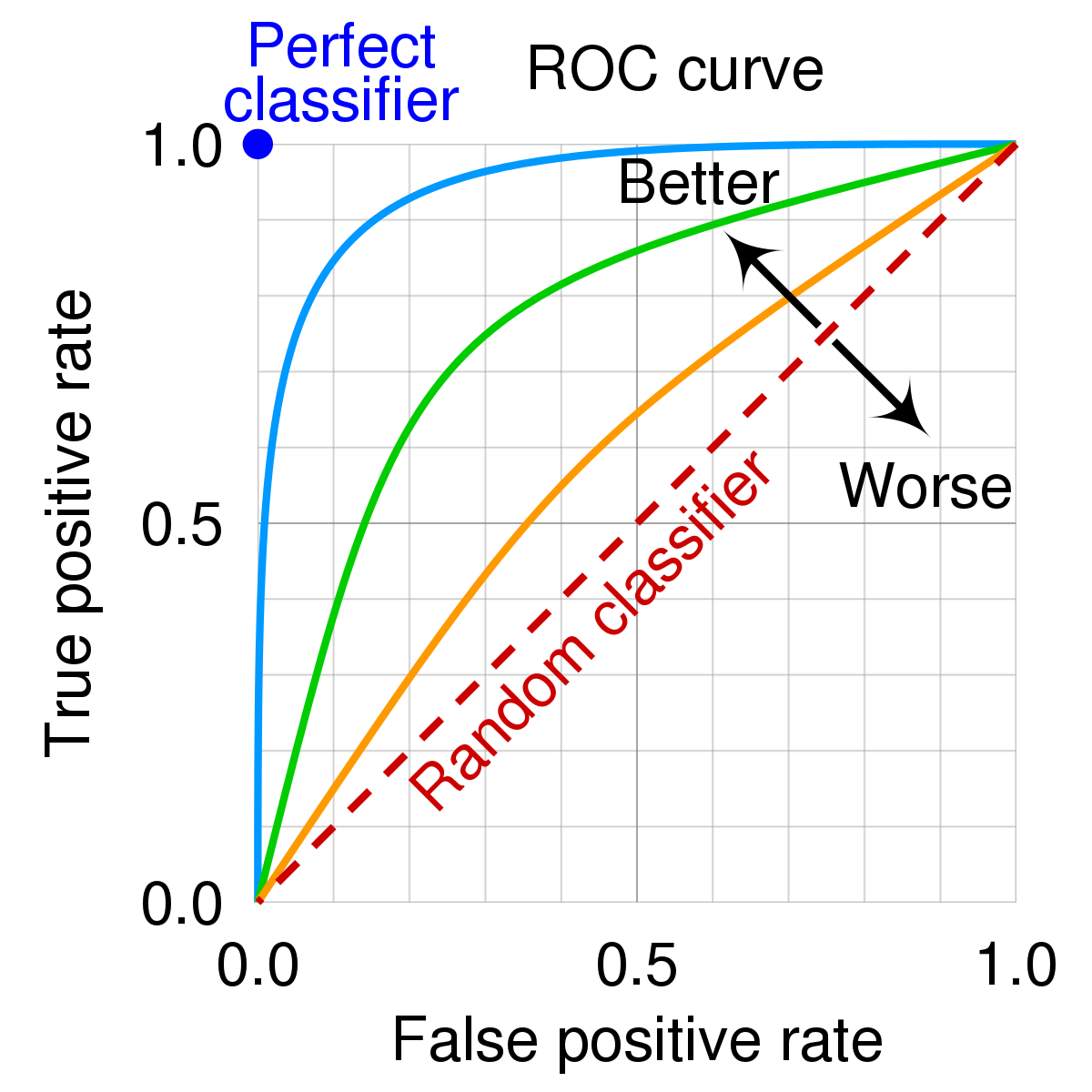
ROC Curve
분류 model의 성능을 시각적으로 평가하는 그래프
-
True Positive Rate (TPR) 또는 Recall (민감도, Sensitivity)
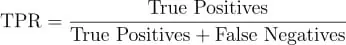
-
False Positive Rate (FPR) (1-특이도, 1-specificity)
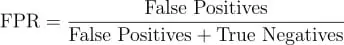
장점
- 다양한 Threshold에서 평가 가능
- 클래스 불균형에 강건한 평가 가능
- 정밀도를 반영하지 않음
AUC (Area Under the Curve)
ROC 곡선 아래의 면적으로, 모델의 성능 지표 중 하나
( 0~1 사이 값을 가짐 )
Log Loss
model이 출력한 확률값과 실제값의 차이를 정량적으로 측정
(값이 작을 수록 좋음)
Cross Entropy loss라고도 부름
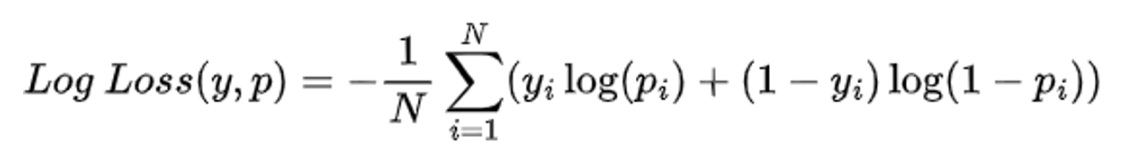
장점
- 확률적 예측이 중요한 문제에 유용 (로지스틱 회귀, 신경망)
단점
- 작은 오류에도 민감하게 평가 가능
- 확률 출력이 필수적이어서, 순위만 제공하는 모델에서 사용 어려움
2. Multiclass Classification Evaluation
: 다중 클래스 분류에서 사용되는 평가 지표
Accuracy (정확도)
(앞에서 설명함)
Marcro F1
F1 Score로 전체 클래스의 성능을 균등하게 평가할 때 사용
각 class별 F1 Score를 먼저 계산하고, 동일한 가중치로 평균낸 값
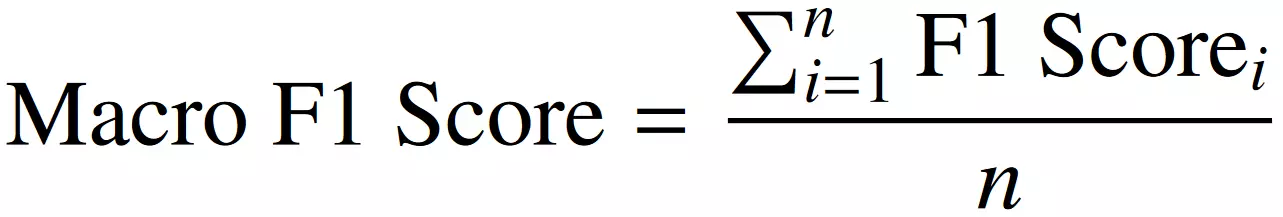
장점
- 모든 class에 동일한 중요도를 부여하여, 소수 클래스의 성능을 과소평가하지 않음
- 각 class별 성능을 동등하게 고려해야하는 문제에서 유리
단점
- 빈도가 적은 class의 결과가 왜곡될 수 있음
Weighted F1 Score
class의 빈도가 불균형할 때, 데이터의 개수가 많은 class는 비중이 크게, 적은 class는 비중을 적게 평가하는 지표
각 class별 출현 빈도를 반영하여 현실적인 성능 평가 가능
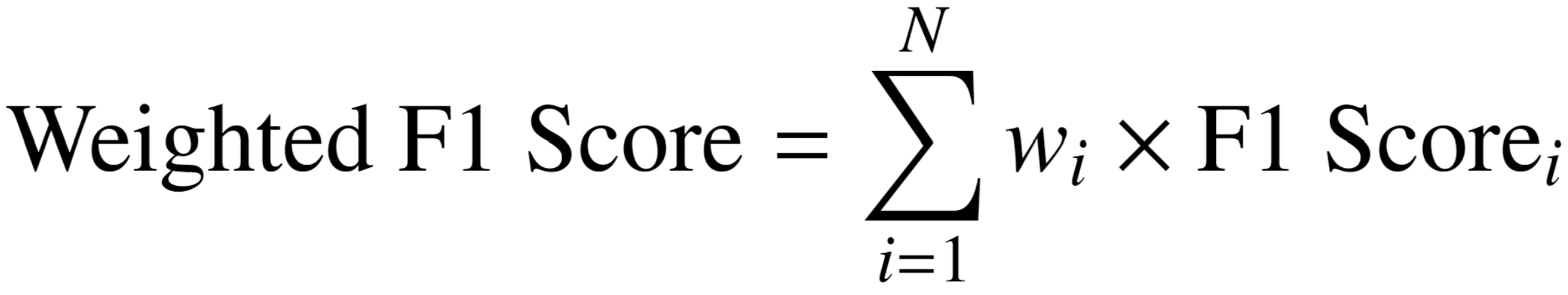
장점
- class 불균형이 있는 data에서 실제 성능을 정확하게 평가
단점
- 데이터 빈도 수가 매우 낮은 class의 성능이 점수에 아예 반영 안 될 수도 있음(다른 지표를 추가로 고려해야함)
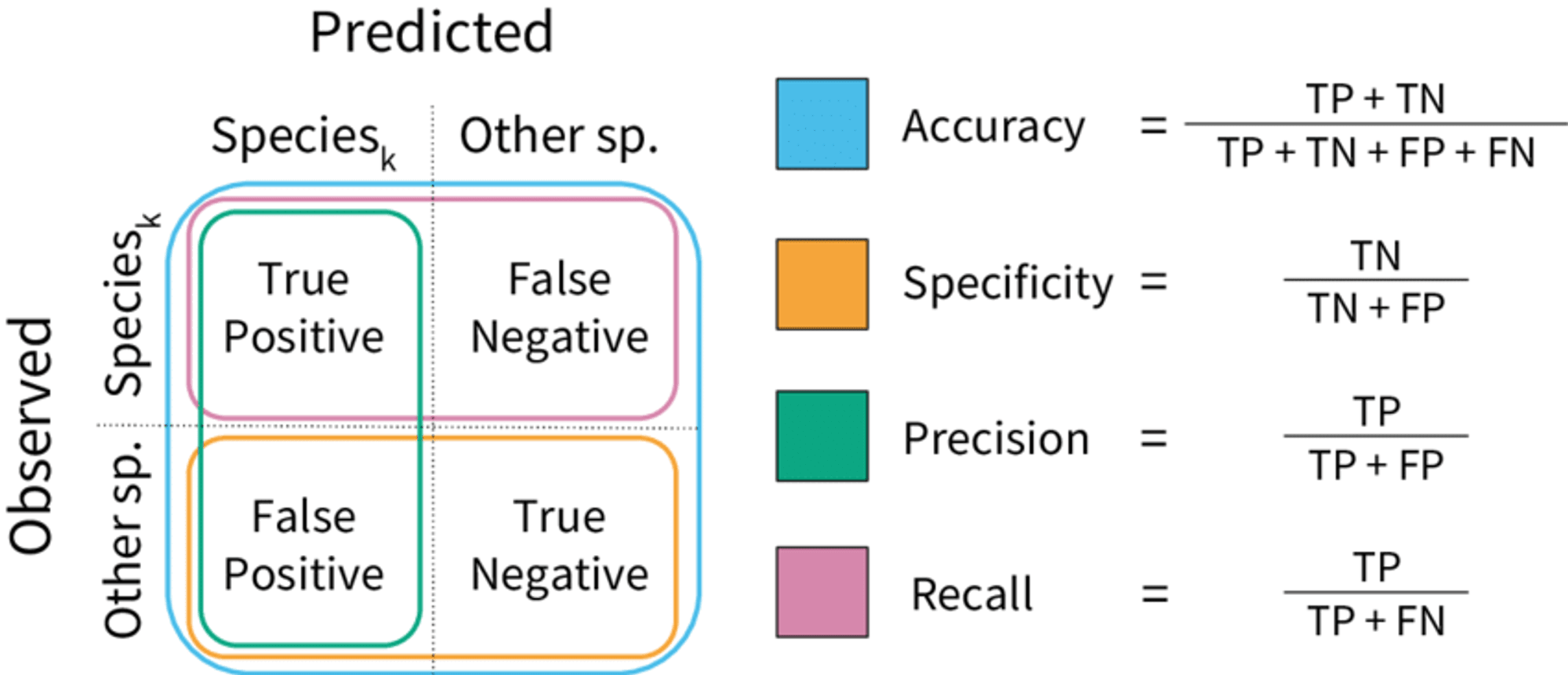
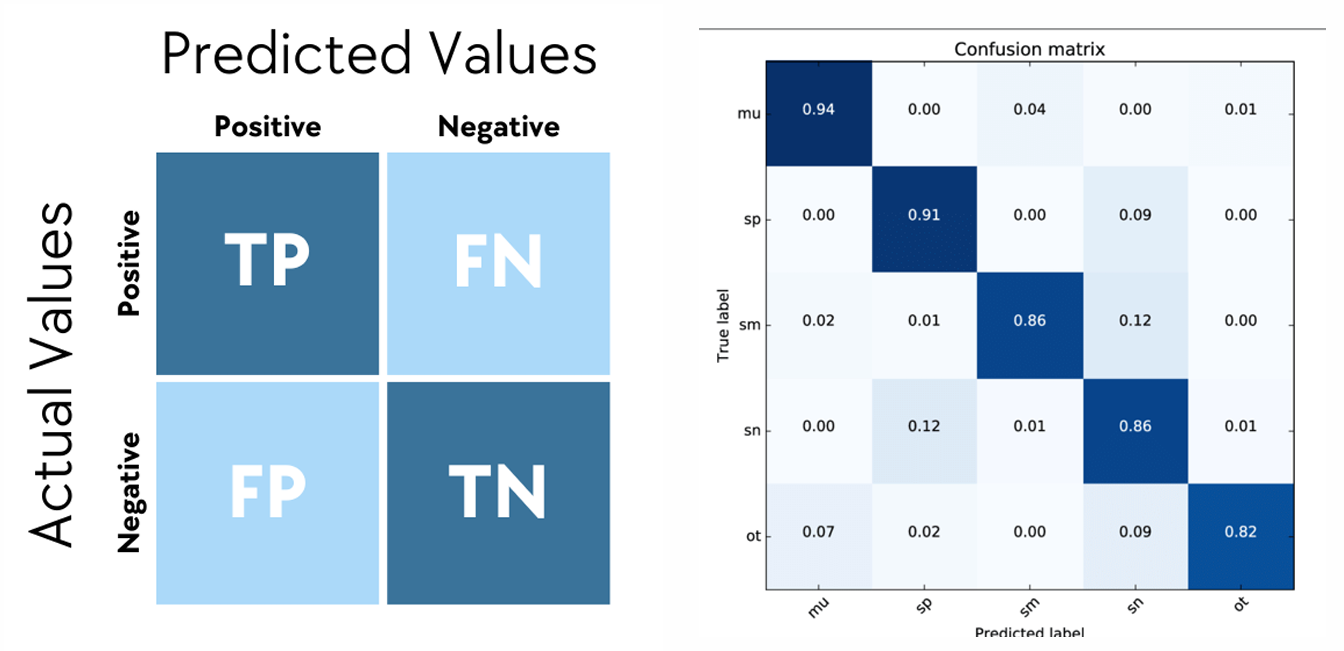
Confusion Matrix
모델의 성능을 시각적으로 평가할 때 사용되는 표(지표)
장점
- 매우 직관적이고 명확하게 시각화
- class 간 혼동 패턴을 쉽게 파악
- 다른 성능 지표(Accuracy, F1 score)를 빠르게 계산 가능
Top-K Accuracy
예측 결과가 상위 K개 class 중 포함되는지 평가
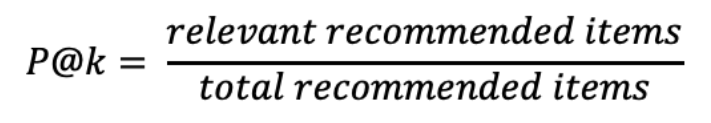
장점
- model이 실제 정답에 근접한 예측을 하고 있는지 평가할 때 사용
- 주로 추천 시스템, 자연어 처리 분야에서 사용
단점
- k값이 너무 크면 평가의 의미가 줄어들 수 있음
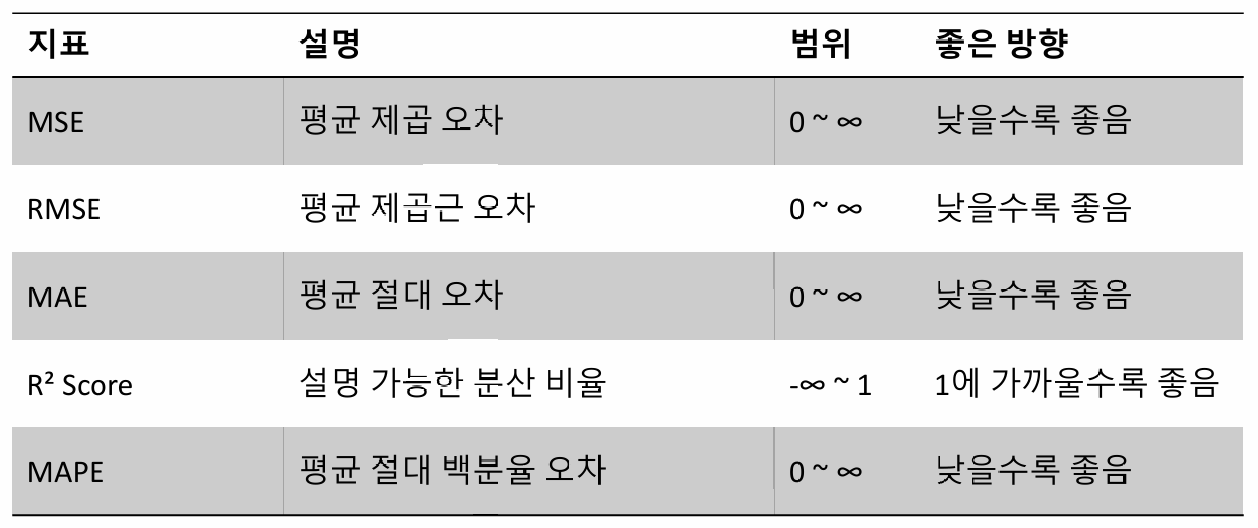
3. Regression Evaluation
: 회귀 문제에서 사용되는 평가 지표 (Loss의 개념)
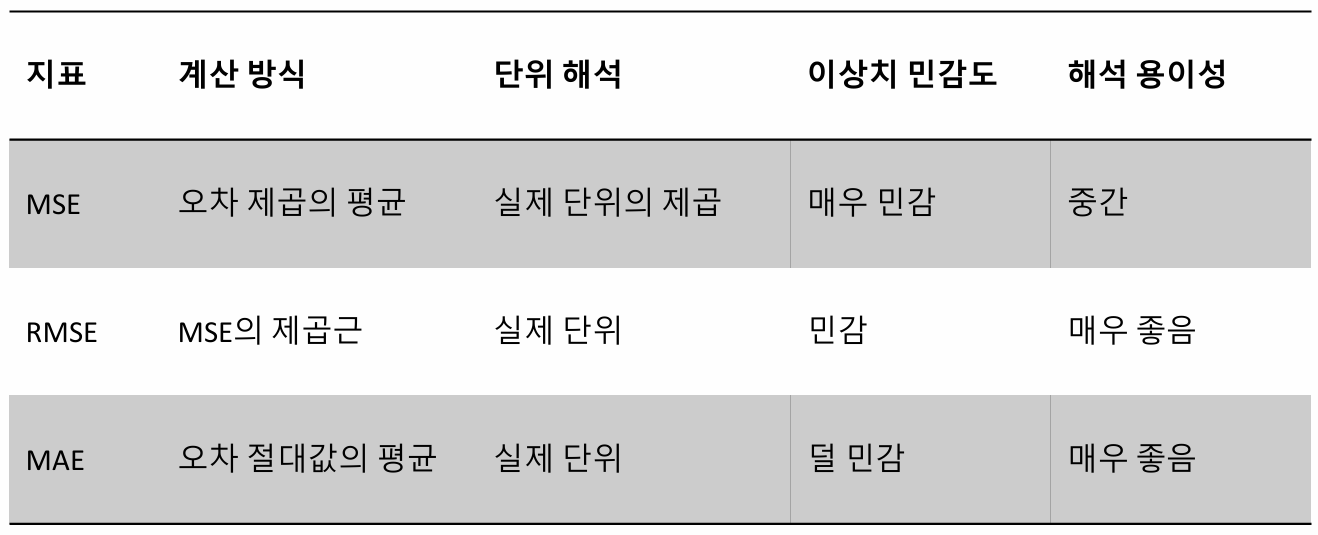
MSE (Mean Squared Error)
예측한 값과 실제 값의 차이를 제곱하여 평균내는 방식
(이상치에 특징이있어 큰실수를 최소화 하도록 유도함)
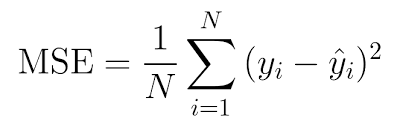
장점
- 계산이 간단하고, 직관적으로 이해 쉬움
- 미분 가능, 최적화 과정에 유리
단점
- 큰 오차에 민감하기에, 이상치에 취약
- 오차 단위가 제곱이므로 실제 단위와 차이 존재
RMSE (Mean Squared Error)
예측값과 실제값의 차이를 제곱하여 평균낸 후, 제곱근을 적용하는 방식
(실제값과 동일한 단위로 표현 가능)
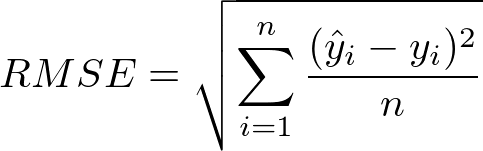
장점
- 계산이 간단하고, 직관적으로 이해 쉬움
단점
- 여전히 큰 오차에 민감, 이상치 취약
MAE (Mean Absolute Error)
예측값과 실제값의 차이를 절대값으로 변환하여 평균으로 계산한 값
(실제값과 동일한 단위로 표현 가능)
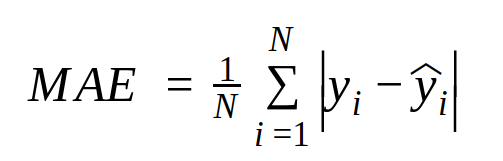
장점
- 계산이 간단하고, 직관적으로 이해 쉬움
- 이상치에 덜 민감하고, 안정적임
단점
- 미분 불가능한 지점이 존재해, MSE보다 덜 효율적
- 큰 오차에 집중해야 할 상황에서는 다른 것과 병행 필요
MSE vs RMSE vs MAE 비교
MSE : 매우 큰오차를 줄이는데 집중할 경우
RMSE : 큰 오차에 집중하면서 안정적인 분석 필요한 경우
MAE : 안정적인분석이필요할경우
(R-Squared, 결정계수)
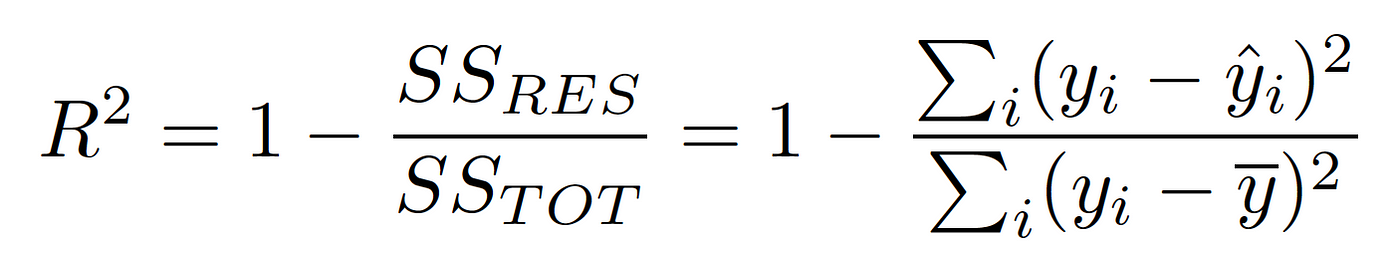
장점
- 직관적이고, 이해 쉬움
- 서로 다른 model의 성능을 비교할 때 유용
단점
- 오직 선형관계만 반영, 비선형 model에서는 제한적
- data의 개수가 적을 때는 값이 높게 나오는 경우 있어, 과적합에 주의
- 변수가 많아질 수록 증가하기에, 주의 필요
Adjusted (조정된 결정계수)
변수가 많아질 수록 값이 증가하는 문제를 해결하기 위해 조정된 결정계수
(변수가 많을 때 유용함)

장점
- 변수 개수를 고려하여, model의 실제 설명력을 정확히 반영
- overfitting을 방지하는데 효과적
단점
- data의 개수가 적을 경우 정확도 떨어짐
MAPE (Mean Percentage Error)
실제값과 예측값의 차이를 절대값 백분율로 변환하여 평균낸 값
백분율로 표현하기에, 매우 직관적인 지표
(ex. MAPE=10%라면 model이 10% 오차)
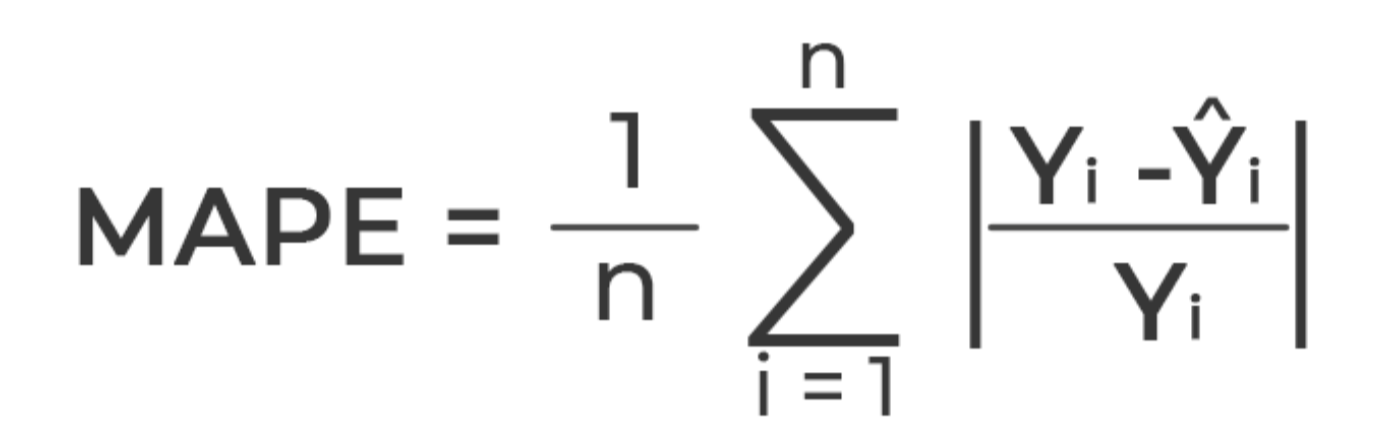
장점
- 서로 다른 규모를 가진 data를 비교할 때 유리함
단점
- 실제값이 0 또는 매우 작은 값일 때 급격하게 MAPE 커짐
- 실제값이 음수일 경우, 사용 어려움
- data가 0에 가까울 경우, MAE 혹은 RMSE 추가로 고려해야됨
4. Evaluation Example
Example 1. Top-K Accuracy
data 1,3에 model의 Top3예측은 정답을 포함하고 있기에

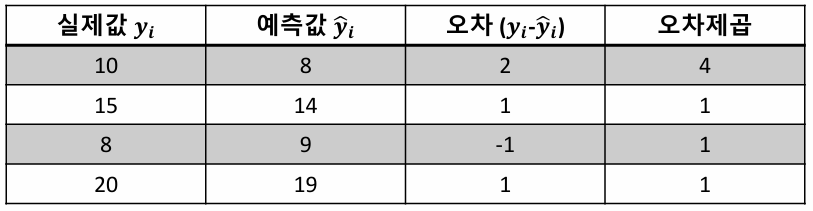
Example 2. (R-Squared)

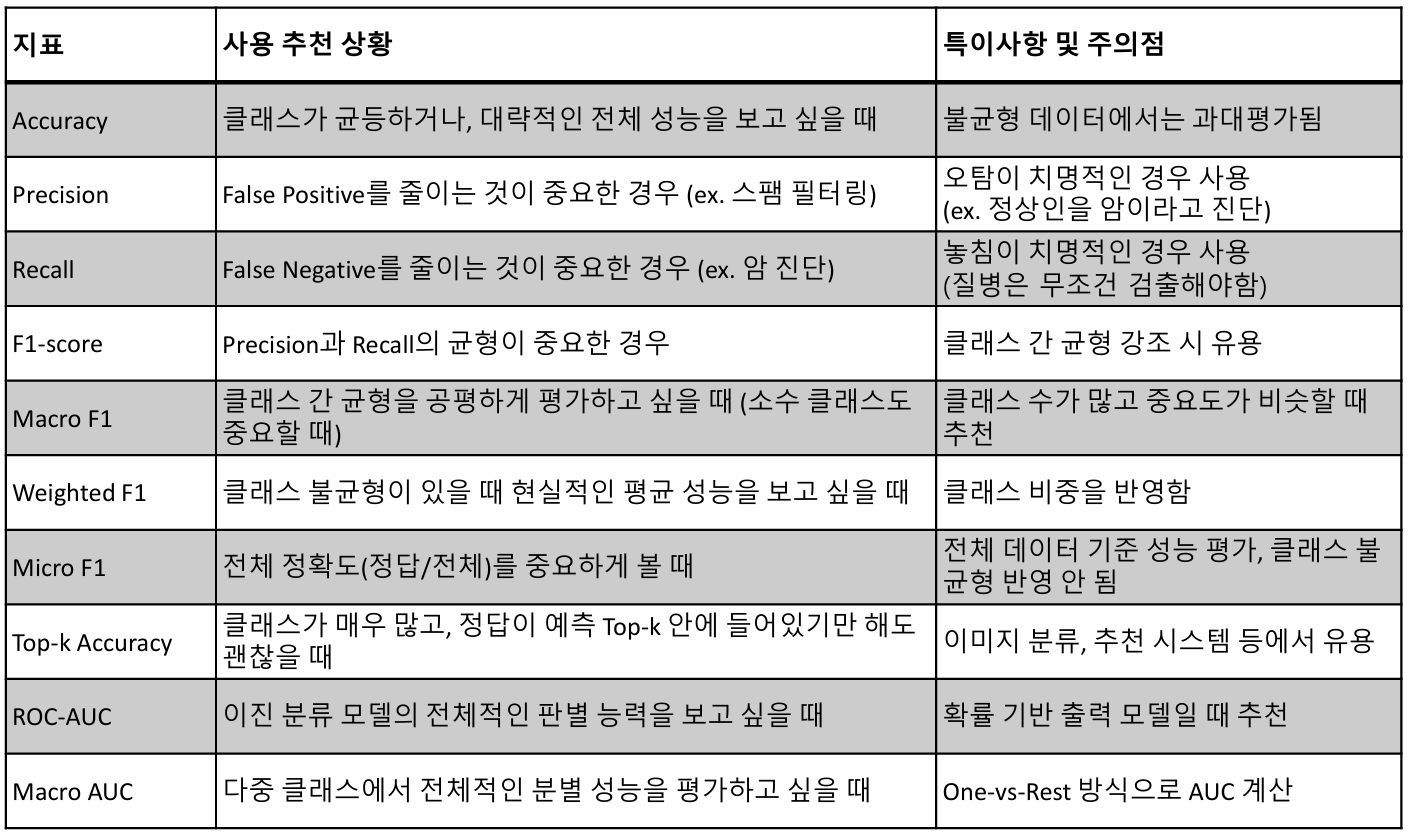
Classification Evaluation Summary
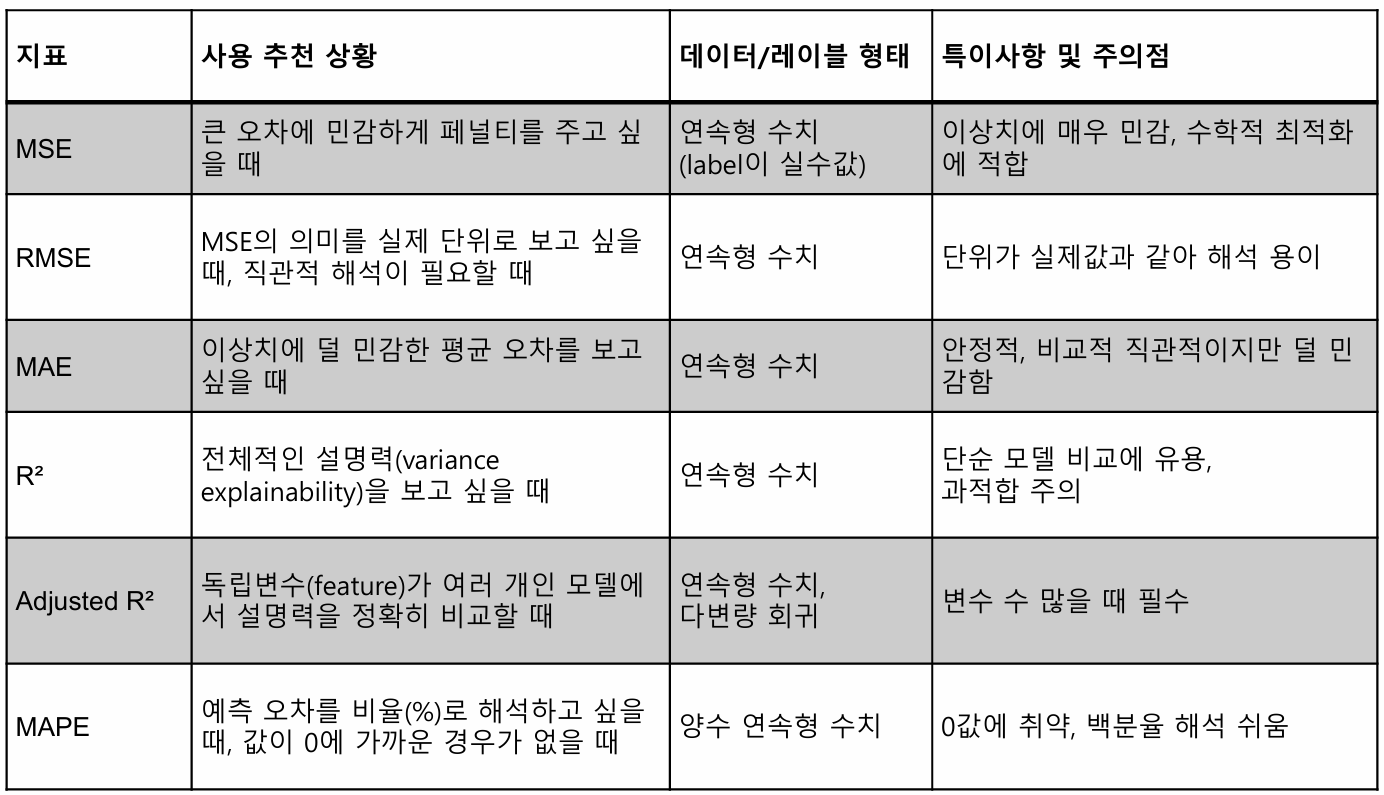
Regression Evaluation Summary