Uniform-Cost Search (일정량 탐색, UCS)는 상태 공간에서 최소 비용 경로를 찾기 위한 탐색 알고리즘 중 하나 이다. 이 알고리즘은 경로의 비용을 고려하여 탐색을 수행하며, 시작 상태에서 목표 상태로 이르는 최소 비용 경로를 찾기 위해 사용된다.
UCS는 최단 경로 문제를 해결하기 위한 효과적인 알고리즘으로 사용된다. 그러나 메모리 사용량이 중요한 경우나 상태 공간이 매우 큰 경우, 다른 탐색 전략을 고려해야 할 수 있다.
UCS는 목표 상태까지의 최소 비용 경로를 찾기 위해 더 많은 계산을 수행하므로, 경로 비용을 중요하게 생각해야 하는 문제에 적합하다.
특징
- 경로 비용(Path Cost) 고려
- 일정량 탐색은 경로의 비용을 중요하게 고려한다.
- 각 상태까지 이르는 데 필요한 비용을 누적하여 최소 비용 경로를 찾는다.
- 우선순위 큐(Priority Queue) 사용
- 일정량 탐색은 우선순위 큐(Priority Queue) 자료 구조를 사용하여 상태를 저장하고 탐색한다.
- 우선순위 큐를 사용하므로 현재까지 경로의 비용이 낮은 상태를 먼저 탐색한다.
- 완전성(Completeness) 보장
- 일정량 탐색은 완전성(Completeness)을 보장한다.
- 목표 상태가 존재하는 한 항상 목표 상태를 찾아낸다.
- 최적성(Optimality) 보장
- 일정량 탐색은 경로의 비용을 고려하여 가장 낮은 비용의 경로를 찾아낸다. 따라서 최적 경로를 찾는데 사용할 수 있다.
동작 단계
- 시작 상태를 우선순위 큐에 추가하고 해당 상태까지의 비용을 0으로 설정한다.
- 우선순위 큐에서 비용이 가장 낮은 상태를 선택한다.
- 선택한 상태의 자식 상태를 생성하고, 각각의 경로 비용을 누적한 후 우선순위 큐에 추가한다.
- 우선순위 큐에서 다시 가장 낮은 비용을 갖는 상태를 선택하고 반복한다. 이를 반복하여 목표 상태에 도달하면 최소 비용 경로를 찾은 것이다.
Example: Romania
- Sibiu에서 Bucharest까지 가는 최단 경로를 구하는 문제
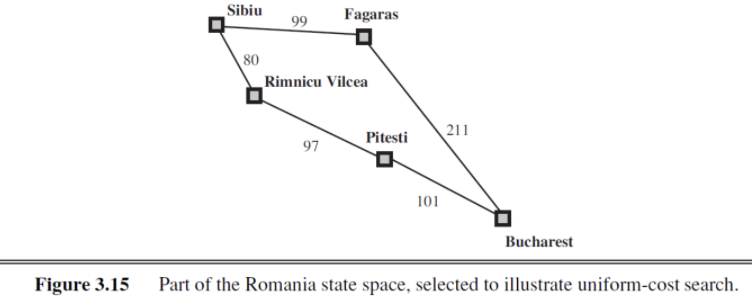
1. Sibiu는 Expand, Fagaras와 Rimmicu는 Frontier에 존재한다.
F(99)와 R(80) 중 비용이 작은 R을 Frontier에서 꺼내고, Goal Test 후, Expand한다.
현재 Frontier: [Fagaras(99)], Expand: [Sibiu(0), Rimicu(80)]
2. Rimnicu의 자식인 Pitesti를 Frontier에 넣는다.
현재 Frontier: [Fagaras(99), Pitesti(80+97=177)], Expand: [Sibiu(0), Rimnicu(80)]
3. Frontier에서 Fagaras를 꺼내고, Goal Test 후 Expand한다. 또한, 자식인 Bucharest를 Frontier에 넣는다.
현재 Frontier: [Pitesti(177), Bucharest(99+211=310))], Expand: [Sibiu(0), Fagaras(99)]
4. Frontier에서 Pitesti를 꺼내고, Goal Test후 expand한다. 또한 자식인 Burcharest가 이미 Frontier에 있지만 들어있는 비용보다 더 작기 때문에 교체해준다.
현재 Frontier: [Bucharest(278)], Expand: [Sibiu(0), Rimnicu(80), Pitesti(177)]
5. Burcharest를 꺼내고 Goal Test 후 종료한다.
최적 경로: [Sibiu(0), Rimnicu(80), Pitesti(177), Bucharest(278)]- 위 과정에서 볼 수 있듯이 Burcharest는 3번에서 이미 Frontier에 들어갔지만 알고리즘이 종료되지 않는다.
- 만약 Frontier에 넣기 전에 Goal Test를 했더라면 310의 비용으로 알고리즘이 끝났겠지만 Uniform-Cost는 Frontier에서 나올 때 Goal Test를 하기 때문에 310이 아닌 278의 비용으로 종료할 수 있었다.
