탐색 알고리즘 DFS, BFS

seulg1004·2021년 9월 16일

python

💡DFS란

✔️ DFS 코드 예제

인접 리스트 예시

👀 DFS와 플로이드 워셜 함께 사용하기

💡BFS란

✔️ BFS 예제

PythonAlgorisim

목록 보기

6/14

파이썬 개념들은 모두 notion에 대충 정리해뒀는데, 제대로 정리해서 벨로그에 올려둬야지 했었다. 특히 탐색 알고리즘은 이해하기 힘들어서 더 필요성을 느꼈던 것 같다🤔 내겐 아직 먼 탐색 알고리즘이지만...ㅜㅠ

들어가며

DFS, BFS는 Uninformed Search, 즉 정형화되지 않은 탐색이라고 부른다. 이것은 이미 어느 방법이 더 효과적인지 알고 탐색하는 Informed Search 와는 확연히 다른 개념이다. 정해진 메모리와 시간 안에 실행되어야하는 것과는 반대로 어느 방법이 효과적인지 모르기 때문에 더 비효율적인 방식일 수 있다.

저것은 인공지능 교수님께서 말씀해주신 개념이고 코딩테스트에서는 조금 방향이 다르게 사용되는 것 같았다. 물론 최단 경로를 구하는 것은 같았지만, 코테에서의 BFS는 덱을 사용하여 구현하였는데 AI에서의 BFS는 primary queue인 우선순위 큐를 사용해 구현하는 방식이었다.(다익스트라 알고리즘이 생각나는 코드였다..) 알고리즘이 종료될 때까지 값이 큰 노드에 방문하지 못하는 불상사를 방지하기 위해서 A* 알고리즘을 사용하는데, 이 부분을 자세히 짚고 넘어가야 할 것 같아서 이렇게 포스트를 쓴다.

아무튼 본격적으로 DFS, BFS를 알아보기 전에 내가 생각한 둘의 차이는 이것이다. 이렇게 외우니 좀 더 이해가 잘 됐다ㅎㅎ

💡DFS란

DFS는 깊이 우선 탐색, 즉 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이다. 이 설명만 듣고 보면 어려울 수 있는데 인접한 노드 중 값이 작은 것부터 탐색하는 방법이라고 생각하면 된다. 그래프로 나타내면 다음과 같다.

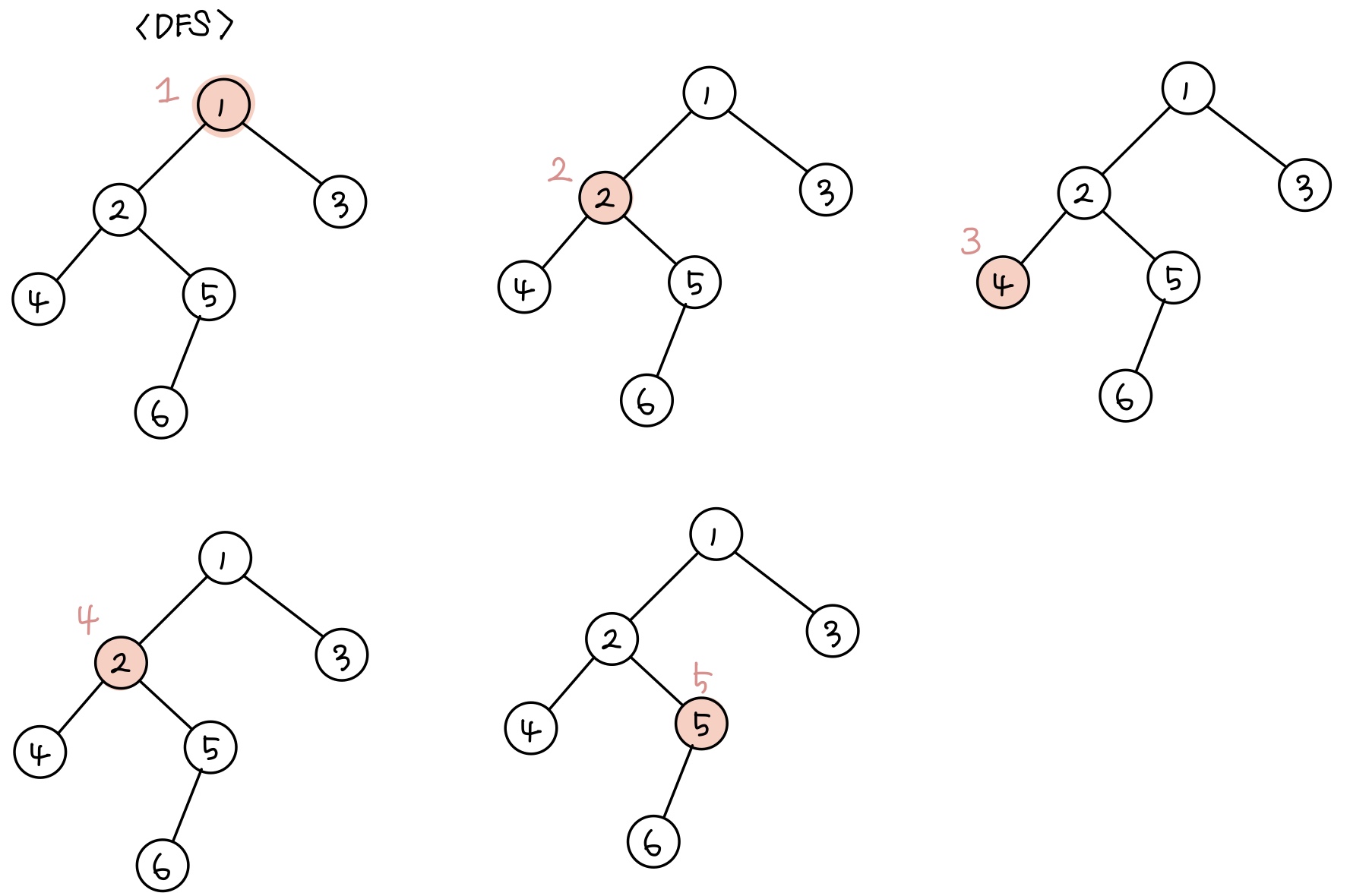
그림에서는 두번째 단계에서 2번 노드를 방문하고 네번째 단계에서 2번 노드를 한 번 더 방문하게 된다. 스택 자료형을 사용하면 실제로 저렇게 코드가 작동이 되겠지만 코드로 작성할 때는 리스트 자료형을 사용한다.

DFS는 모든 노드를 방문하는 '탐색'이 목표이기 때문에 방문 여부를 기록하는 리스트 visited를 활용하여 같은 노드를 다시 방문하지 않게 한다.

다음은 이코테에 있는 DFS 코드 예제이다.

✔️ DFS 코드 예제

def dfs(graph, v, visited):
	# 현재 노드 방문 처리
	# v가 노드.. 
	visited[v] = True
	print(v, end='')
	for i in graph[v]: # 해당 노드에 인접한 노드를 확인
		if not visited[i]: # 그 중 가장 작은 노드가 방문되었는지 확인
			dfs(graph, i, visited) # 그 노드를 이용해 dfs함수 재호출
            
# 노드가 연결된 정보를 2차원 리스트로 표현합
graph = [
	[],
	[2, 3, 8],
	[1, 7],
	[1, 4, 5],
	[3, 5],
	[3, 4],
	[7],
	[2, 6, 8],
	[1, 7]
]

visited = [False]*9

dfs(graph, 1, visited) # 번호가 작은 인접한 노드를 방문하는 dfs 함수 호출

이 예시에서는 연결된 간선들이 모두 같은 비용을 가지고 있다고 가정하고, 작은 번호 순으로 DFS를 진행하였지만 비용이 다를 경우 인접 행렬이나 인접 리스트로 저장하면 편하다.

다음은 인접 리스트 예시이다.

인접 리스트 예시

graph = [[] for _ in range(3)]

# 노드 0에 연결된 노드 정보 저장
graph[0].append((1,7))
graph[0].append((2,5))

# 노드 1에 연결된 노드 정보 저장
graph[1].append((0, 7))

print(graph)
# [[(1,7),(2,5)], [(0, 7)]]

이렇게 튜플 자료형으로 ( 연결된 노드, 비용 ) 을 묶어서 리스트에 저장하면 된다.

여기서 유의할 점은 튜플은 정렬할 경우 첫 번째 인자 기준으로 정렬하게 되는데, 위 예제에서는 노드 번호 순으로 정렬하였다. 그러니까 최단 경로를 구하는 방법이 아니라는 얘기다. 플로이드나 크루스칼과 같이 쓰지 않는 한 탐색 알고리즘은 결코 최단 경로를 구하는 방법이 될 수 없다. 현재 위치해 있는 값을 기준으로 탐색하기 때문인데, 이 이유는 뒤에서 bfs를 설명하면서 하겠다.

그러면 어느 경우에 플로이드와 함께 쓰이게 될까?
https://www.acmicpc.net/problem/17182

사실 이 문제에서 막힌 걸 계기로 이 포스트를 업로드하게 됐다..ㅎ 이걸 풀려면 플로이드와 dfs를 함께 사용해야한다.
일단 모든 행성을 탐사해야하고(dfs) 그 중 가장 최단 경로를 구하는 것(플로이드)이기 때문인데, 여기에서는 행성을 중복 방문할 수 있으므로 방문 표시를 해준 뒤 재귀함수를 호출하면서 방문 표시를 초기화 해주어야한다.

👀 DFS와 플로이드 워셜 함께 사용하기

# 발사되는 위치에서 false, 발사되지 않는 위치에서 true(방문하였다는 표시)
not_visited = [False if i == k else True for i in range(n)]

minval = [INF]

def DFS(r, c, time, depth):
    if depth == n-1: # 깊이가 n-1일 경우,, 그러니까 모든 행성을 방문했을 경우
        minval[0] = min(minval[0], time) # 최솟값 갱신해줌
        return

    if time > minval[0] : # 예외 처리
        return

    for j in range(n):
        if j != c and not_visited[j]:
            not_visited[j] = False
            DFS(c, j, time + arr[c][j], depth+1) # 행성 방문횟수 늘여서 재귀호출 해줌
            not_visited[j] = True # 방문 초기화

첫 번째 예제와 다르게 방문 표시를 다시 지워주는 것을 볼 수 있다. 이렇게 DFS를 호출해주면 처음에 봤던 DFS 그래프 방식으로 작동할 것이다.

문제 <우주 탐사선>은 플로이드로 최단 경로를 갱신해준 뒤 앞 dfs코드를 활용하면 풀 수 있다.

💡BFS란

순차적으로 길을 탐색하는 DFS와 다르게 BFS는 너비 우선 탐색으로, 가까운 노드부터 탐색하는 알고리즘이다. 이 역시 그래프로 나타내면 다음과 같다. 분홍색은 현재 큐에 들어있는 노드, 파란색은 방문한 노드를 나타낸다.

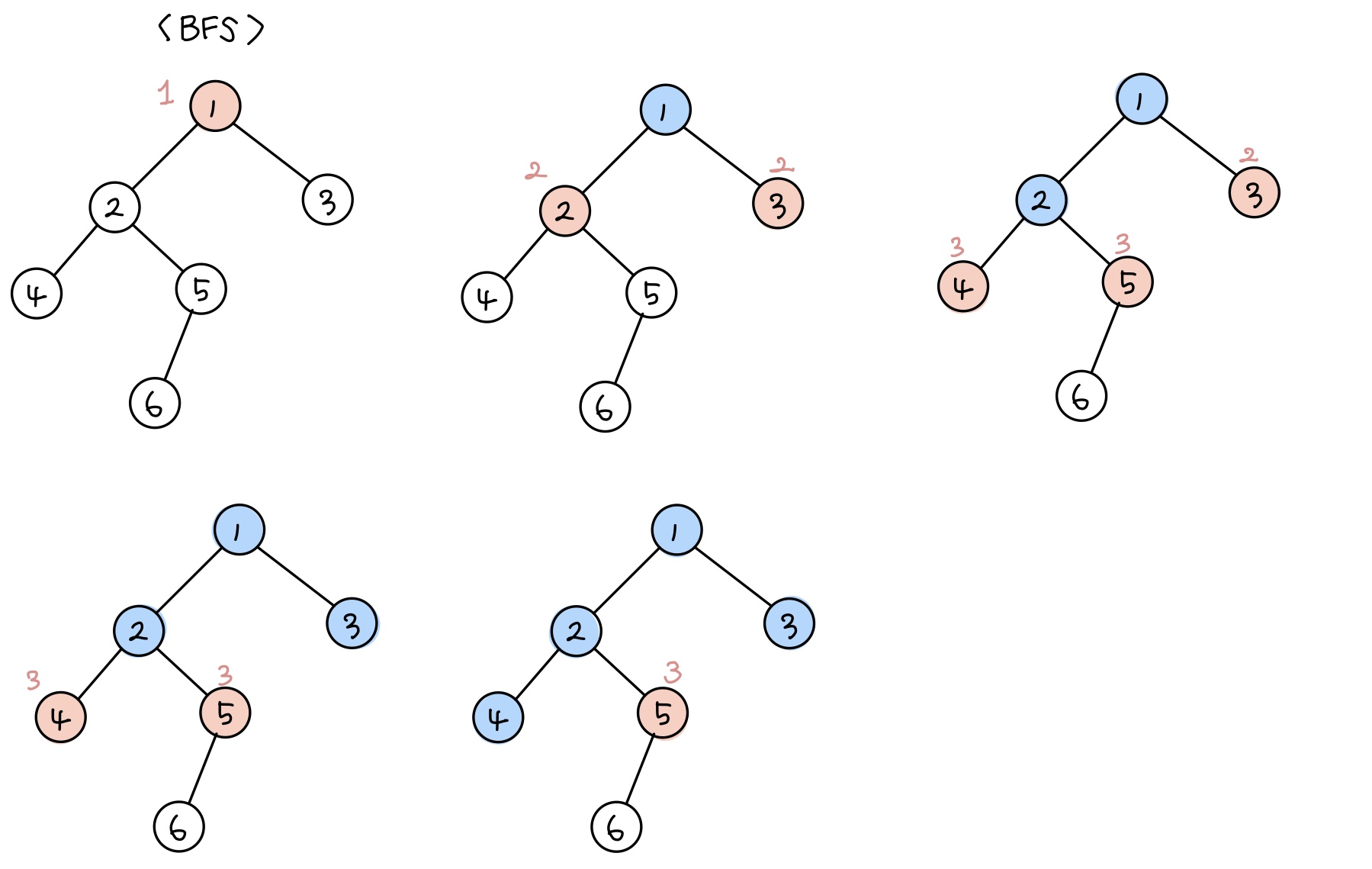
우선순위 큐가 아니라 덱으로 구현한 그래프를 나타냈기 때문에, 덱에 들어간 순서대로 노드가 방문되는 것을 확인할 수 있다. 물론 위와 같은 그래프는 우선순위 큐로 구현해도 같은 흐름으로 흘러갈테지만 보통 그래프는 그렇지 않다.

BFS는 DFS와 달리 덱에서 원소를 넣고, 빼는 방식으로 구현하기 때문에 위, 아래, 오른쪽, 왼쪽으로 갈지 선택하는 그래프에서 자주 사용되는 알고리즘 방법이다.

다음은 이코테에 수록되어있는 BFS 예제이다.

✔️ BFS 예제

from collections import deque

def bfs(graph, start, visited):
	# 큐 구현을 위해 덱 라이브러리 이용
	queue = deque([start]) # 인접한 노드는 모두 덱에 넣어둠 (중복은 제거하겠지)
	visited[start] = True # 방문했다!
	while queue : # 큐가 빌 때까지 반복하는 반복문(반복 조건: 큐가 있을 경우)
		v = queue.popleft() # 큐에서 맨 앞 원소를 하나 뽑아서 출력
		print(v, end='')
		for i in graph[v]: # 그 원소에 인접한 노드를 모두 검사해본다.
			if not visited[i]: # 만약 방문하지 않았으면
				queue.append(i) # 덱에 원소 삽입
				visited[i] = True

bfs(graph, 1, visited)