💡문제를 처음보고 든 생각
다이나믹 프로그래밍에 관련된 문제입니다. 주어진 제한 메모리가 128MB이고 입력값은 10000이하이기 때문입니다. 따라서 주어진 패턴을 분석하고 첫 계단에서 마지막 계단으로 혹은 마지막 계단에서 첫 계단으로 이동하면서 값을 메모이제이션 해야겠다고 생각했습니다.
🔨트러블 슈팅
위에서 언급한 패턴 찾기에서 시간을 많이 소모했습니다. 특히 연속해서 한 칸씩 움직이면 안되었기 때문에 해당 조건이 까다로웠습니다. 마지막 계단에는 무조건 도달해야 한다는 조건 때문에 마지막 계단에 도달하기 위해서는 마지막 계단 한 칸 전 혹은 두 칸 전에서 올라와야 합니다. 저는 이러한 경우의 수를 없애고 싶어서 마지막 계단에서 출발하는 방법을 생각했습니다. 또한 이차원 배열을 이용해 한 칸 움직인 상태인지 한 칸 뛰고 두 칸 움직인 상태인지를 구분해 문제를 해결했습니다. 문제를 해결하고 다른 분들의 풀이를 검색해 보았는데 본질적으로 동적 프로그래밍을 사용하는 것은 같지만 방법이 조금 달랐습니다. 제 풀이는 정석 같은 느낌은 아니지만 이렇게도 풀 수 있구나 하는 식으로 포스팅을 남깁니다.
💻풀이 방법
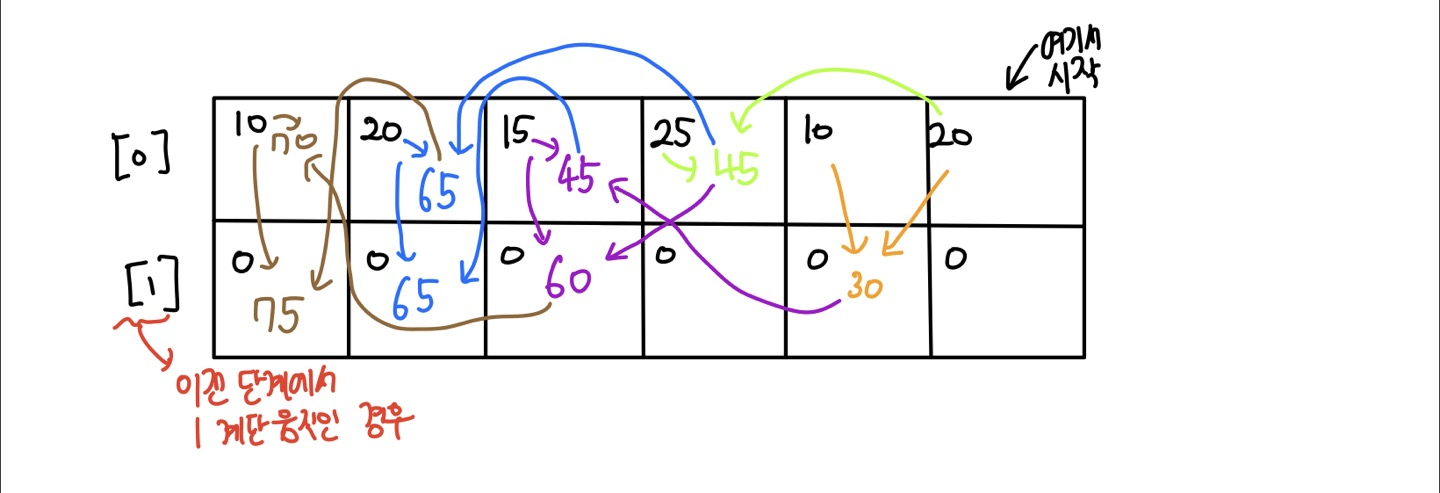
위의 그림과 같이 2차원 배열을 선언하고 1번째 행에는 2계단 전에 온 값을 저장하고 2번째 행에는 1계단 전에 온 값을 저장해서 연속된 세 개의 계단을 모두 밟아서는 안 된다는 조건을 만족시키며 계산하려고 했습니다. 시작 계단이 아닌 마지막 계단부터 출발하여 밑으로 내려가면서 계산을 했고 색깔 별로 단계를 나타냈습니다.
정석적이고 깔끔한 풀이는 계단의 숫자 값을 arr배열에 저장하고 현재 계단까지의 숫자의 합 최댓값을 저장하는 dp배열을 하나 만드는 것입니다. i번째 계단에 도착하기 위해서는 (i-1)번째 계단에서 i번째 계단으로 올라가거나 (i-2)번째 계단에서 i번째 계단으로 올라가야 하므로 두 개의 값 중 최댓값을 dp[i]에 저장하면 됩니다. 단, (i-1)번째 계단에서 올라오는 경우 반드시 (i-3)번째 계단에서 올라와야 하므로(연속된 세 개의 계단을 모두 밟아서는 안 된다는 조건때문에) dp[i-3]+arr[i-1]+arr[i]가 됩니다. (i-2)번째 계단에서 올라오는 경우는 dp[i-2]+arr[i] 이고 둘 중 더 큰 값을 dp[i]에 저장하면 됩니다.
📝소스코드
import sys
input = sys.stdin.readline
n = int(input())
# 계단의 개수를 입력 받는다.
arr = []
# 계단에 쓰인 점수를 리스트로 입력 받는다.
for _ in range(n):
arr.append([int(input()),0])
# n이 1이거 2인 경우는 예외처럼 하드코딩한다.
if n==1:
print(arr[0][0])
elif n==2:
print(arr[0][0]+arr[1][0])
# n이 3 이상인 경우
elif n>=3:
arr[n-2][1] = arr[n-1][0] + arr[n-2][0]
arr[n-3][0] += arr[n-1][0]
for i in range(n-3):
arr[n-4-i][1] = arr[n-4-i][0] + arr[n-3-i][0]
if arr[n-2-i][1] >= arr[n-2-i][0]:
arr[n-4-i][0] += arr[n-2-i][1]
else:
arr[n-4-i][0] += arr[n-2-i][0]
print(max(arr[0][0], arr[0][1], arr[1][0], arr[1][1]))하세요