Algorithm
1.[백준][Python] 9184번 신나는 함수 실행

문제 링크단계별 문제풀이에서 동적계획법에 있는 문제였고 문제 안에서 "위의 함수를 구현하는 것은 매우 쉽다. 하지만, 그대로 구현하면 값을 구하는데 매우 오랜 시간이 걸린다."라는 구절 때문에 다이나믹 프로그래밍과 메모이제이션(Memoization)에 대해서 떠올렸습니
2.[백준][Python] 1904번 01타일
규칙성이 있을 것 같다는 생각이 들었습니다. 보통 규칙성 있는 경우 점화식 형태로 나타낼 수 있고 이를 재귀함수로 풀되, 제한 시간이 0.75초이므로 메모이제이션을 이용하면 시간 제한에 걸리지 않을 것이라고 생각했습니다.규칙을 찾기 위해 크기 N=1,2,3...인 경우
3.[백준][Python] 1149번 RGB거리

💡문제를 처음 보고 든 생각 > 처음 문제를 보고 예외 처리를 어떤식으로 해야할 지 전혀 감이 잡히지 않았습니다. 그동안 다이나믹 프로그래밍에서는 다양한 경우들을 새로운 자료구조를 만들어 저장한 뒤 꺼내 쓰는 방식이었기 때문에 계속 그러한 방향성으로 생각했습니다.
4.[백준][Python] 2579번 계단 오르기
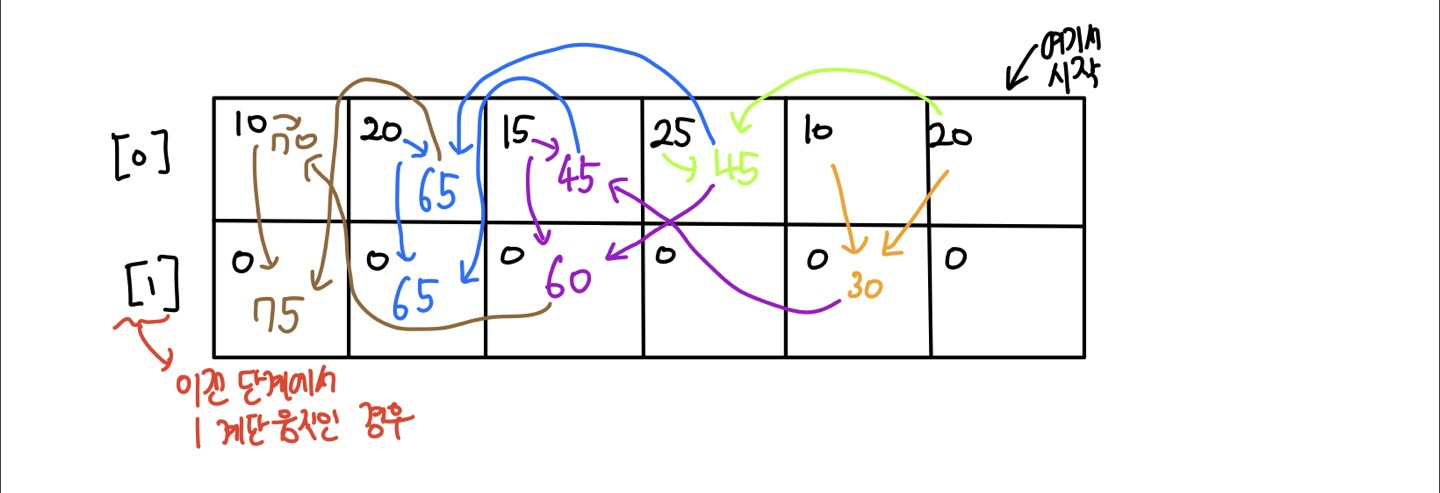
다이나믹 프로그래밍에 관련된 문제입니다. 주어진 제한 메모리가 128MB이고 입력값은 10000이하이기 때문입니다. 따라서 주어진 패턴을 분석하고 첫 계단에서 마지막 계단으로 혹은 마지막 계단에서 첫 계단으로 이동하면서 값을 메모이제이션 해야겠다고 생각했습니다.위에서
5.[백준][Python] 15650번 N과 M(2)

파이썬에는 굉장히 다양한 라이브러리들이 존재한다. 이러한 라이브러리들은 문제를 굉장히 쉽게 해결하는데에 도움을 준다. 15650번 같은 경우도 파이썬의 특정 라이브러리를 이용하면 굉장히 쉽게 풀린다.바로 itertools라는 라이브러리이다. 해당 라이브러리에는 comb
6.[백준][Python] 15651번 N과 M(3)
해당 문제는 15650번과 같이 라이브러리를 불러와서 풀지 않고 dfs를 이용해 정석적으로 해결하였다.핵심 원리는 리스트인 arr에 있다. 빈 arr에 dfs를 수행하면 입력받은 M의 크기와 arr의 길이가 같아질 때까지 append가 일어난다. 그 뒤 M의 크기와 a
7.[백준][Python] 9663번 N-Queen

백트래킹 기법을 사용했다. 1행 1열부터 퀸을 배치하고 2행으로 넘어가 1열부터 퀸을 배치하고 퀸을 배치할 수 있는 조건이면 다음 행으로 넘어가고 배치할 수 없는 조건이면 다음 열로 넘어가는 방식이다. 이런 식으로 마지막 행까지 퀸이 배치가 되면 결과값에 +1을 해주는
8.[백준][Python] 1629번 곱셈

지수의 성질을 이용한 분할 정복과 나머지(Modulo) 연산자의 분배 법칙을 이용해야 한다.A와 B값에 들어갈 수 있는 수는 21억 가량 되기 때문에 A^B를 직접 계산해서 문제를 해결할 수는 없다. 따라서 A^B를 분할해야 한다.만약 B가 짝수이면 예를 들어 2^10
9.[백준][Python] 11279번 최대 힙

파이썬에서는 heapq 라이브러리를 통해 힙을 굉장히 간단하게 구현할 수 있다. 먼저 heapq를 import해주어야 한다.힙에서 가장 중요한 pop과 push 키워드는 다음과 같다.파이썬의 heapq라이브러리는 기본적으로 최소 힙을 구현한다. 따라서 최대 힙을 만들기
10.[백준][Python] 1665번 가운데를 말해요

처음에는 규칙성 문제인줄 알고 최대 합을 구현한 뒤 힙의 원소의 개수의 절반만큼 pop을 해서 중간 값을 찾으려고 했다. -> 시간 초과도저히 모르겠어서 검색해서 방법을 알아냈다. 최대힙과 최소힙을 모두 이용하는 것인데 최대힙 구현할 때 튜플을 썼는데 값을 변경해야 되
11.[백준][파이썬] 14226번 이모티콘

bfs로 접근했으나 막혔다..! 이 문제에서 눈여겨 보아야 할 것은 2가지이다. 바로 현재 화면에 나타난 이모티콘의 개수와 클립보드에 저장되어 있는 이모티콘의 개수이다. 이를 어떤식으로 처리해야 할 지 몰라서 검색을 통해 해결했다. 문제 만든 사람은 진짜 천잰가싶다..
12.[백준][파이썬] 13549번 숨바꼭질 3

기존의 숨바꼭질과 다른 점은 2배로 이동할 때는 가중치가 0이라는 것이다. 그래서 그냥 graphnx = graphx+1부분을 graphnx=graphx로 처리하면 똑같은 것 아닌가하고 제출했는데 틀렸다.틀린 이유는 for문에서의 순서였다. 이 문제에는 3가지의 경우가
13.[백준][파이썬] 6603번 로또

파이썬의 라이브러리 중 순열, 조합을 가져와서 풀면 굉장히 짧고 쉽게 풀리지만 코딩 테스트에서는 해당 라이브러리를 허용하지 않을 수 있을 뿐더러 이 문제의 의도는 dfs 재귀를 활용한 브루트 포스이므로 dfs를 이용해 풀었다.일단 뽑은 번호를 저장하고 추후에 결과로 출
14.[백준][파이썬] 11066번 파일 합치기

dp 문제이다. 핵심은 dpi를 i번째 파일부터 j번째 파일을 합쳤을 때 최솟값이라고 두고 푸는 것이다. dp1, dp2, dp3, ... dpii+1은 연속된 두 개의 파일을 합치는 것으로 파일 i와 i+1의 크기를 단순히 합친 것과 같다.dp1와 같은 경우 dp1+
15.[알고리즘][파이썬] 다익스트라 알고리즘

그래프를 이용한 알고리즘으로 최단 경로를 구하는 대표적인 알고리즘 중에 하나이다. 다익스트라가 만들어서 다익스트라 알고리즘이다. 하나의 특정 노드에 대해서 모든 노드까지의 최단 경로를 알 수 있으며 다음과 같은 특징이 있다.가중치가 음수이면 안된다. -> 가중치의 합을
16.[알고리즘][파이썬] 벨만-포드 알고리즘

그래프를 사용하는 최단거리 알고리즘 중 하나이다. 알고리즘은 배워도 배워도 끝이 없다. 하나 배우면 앞에 배운거 까먹고 ㅎㅎ.. 그래서 이렇게 기록을 해놔야 한다. 다익스트라 알고리즘이라는 많이들 사용하는 알고리즘이 있는데 왜 벨만-포드 알고리즘을 써야하는 경우가 생기
17.[알고리즘][파이썬] 플로이드-와셜 알고리즘
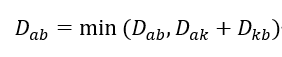
앞서 공부한 다익스트라 알고리즘과 벨만-포드 알고리즘이 특정 노드로부터의 최단거리를 구할 수 있는 알고리즘이었다면 플로이드-와셜 알고리즘은 모든 노드 사이의 최단거리를 구할 수 있다. 이렇게 말하면 더 어려운 알고리즘일 것 같지만 앞의 알고리즘들에 비해서 구현 난이도는
18.[프로그래머스][Python] 가장 큰 수

먼저 주어진 수들을 합칠 수 있는 방법을 모두 나열한 뒤 가장 큰 값을 찾는 것은 안됩니다. 제한 사항에 "numbers의 길이는 1 이상 100,000 이하입니다."가 있기 때문에 최악의 경우 100000!만큼 연산을 해야 하고 이는 시간 초과를 발생시킬 수 있는 너
19.[Python] 중요하지만 헷갈리는 문법들을 정리해보자!

코딩 테스트를 경험하다 보면 외부 IDE를 사용하면 안되는 시험이 종종 있습니다. 당장 토요일에 있을 부스트캠프 코딩 테스트에서도 외부 IDE를 사용하면 안된다고 합니다. 문제는 이러한 경우 시간을 굉장히 단축시킬 수 있지만 항상 사용되는 문법은 아니라 자주 까먹는 문