💡 플로이드-와셜 알고리즘이란?

앞서 공부한 다익스트라 알고리즘과 벨만-포드 알고리즘이 특정 노드로부터의 최단거리를 구할 수 있는 알고리즘이었다면 플로이드-와셜 알고리즘은 모든 노드 사이의 최단거리를 구할 수 있다. 이렇게 말하면 더 어려운 알고리즘일 것 같지만 앞의 알고리즘들에 비해서 구현 난이도는 낮은 편이다.

🤔 어떻게 구현하지?

핵심 원리는 특정 노드를 거쳐가는 경우의 거리값과 현재 저장되어 있는 최단거리 값을 비교해서 값을 갱신하는 것이다. 이를 점화식으로 나타내면 다음과 같다.

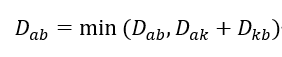
D는 거리로 기존에 저장되어 있던 a노드에서 b노드로 가는 거리를 아래 첨자로 표현한 것이다. 점화식을 사용해 문제를 부분적으로 해결할 수 있고 최소값을 그래프의 배열에 메모이제이션하기 때문에 플로이드-와셜 알고리즘은 다이나믹 프로그래밍에 속한다. 노드의 개수가 K개라면 K개의 노드를 돌면서 모든 노드들을 비교해야 하기 때문에 삼중 반복문을 사용한다. 따라서 시간복잡도가 다익스트라 알고리즘에 비해 크기 때문에 조건을 잘 보고 사용해야 한다. 보통 노드가 500개 이하이고 문제에서 모든 노드들 사이의 최단경로를 구해야한다고 할 때 사용하는 것 같다.

알고리즘	특징	시간복잡도
다익스트라	특정 노드에 대한 다른 노드까지의 최단거리, 가중치는 양수로만 이루어져야 함	$O(\|E\|+\|V\|log \|V\|)$
벨만-포드	특정 노드에 대한 다른 노드까지의 최단거리, 음수가 포함된 가중치까지 커버 가능	$O(\|V\|\|E\|)$
플로이드-와셜	모든 노드 사이의 최단거리를 구할 수 있음, 음의 가중치가 포함되어도 사용 가능	$O(\|V^3\|)$

💻 구현해보자!

백준에서 플로이드-와셜 알고리즘을 사용하는 대표적인 문제이다. 11404번이다.

import sys
input = sys.stdin.readline

INF = 1e9

n = int(input())
m = int(input())

# 그래프 배열 만들고 자기 자신은 0으로 설정
graph = [[INF]*(n+1) for _ in range(n+1)]
for i in range(1, n+1):
    for j in range(1, n+1):
        if i == j:
            graph[i][j] = 0

# 시작 도시, 도착 도시, 버스 한 번 타는데 필요한 비용을 입력받아 graph에 저장
# 이 때 시작 도시와 도착 도시를 연결하는 노선은 하나가 아닐 수 있으므로 같은 노선일 경우 최솟값을 저장
for i in range(m):
    a, b, c = map(int, input().split())
    if graph[a][b] > c:
        graph[a][b] = c

# 플로이드-와셜 알고리즘
# 특정 노드 k를 거쳐가는 경우를 생각해서 k를 안거치는 경우의 값과 k를 거치는 경우의 값을 비교해서 갱신
for k in range(1, n+1):
    for a in range(1, n+1):
        for b in range(1, n+1):
            graph[a][b] = min(graph[a][b], graph[a][k]+graph[k][b])

for i in range(1, n+1):
    for j in range(1, n+1):
        if graph[i][j] >= INF:
            print(0, end=' ')
        else:
            print(graph[i][j], end=' ')
    print()