백준 17779번 게리맨더링2 삼성 SW역량테스트 (Python, 구현, 완전탐색)

백준 17779번 게리맨더링2 문제 바로가기

문제 이해

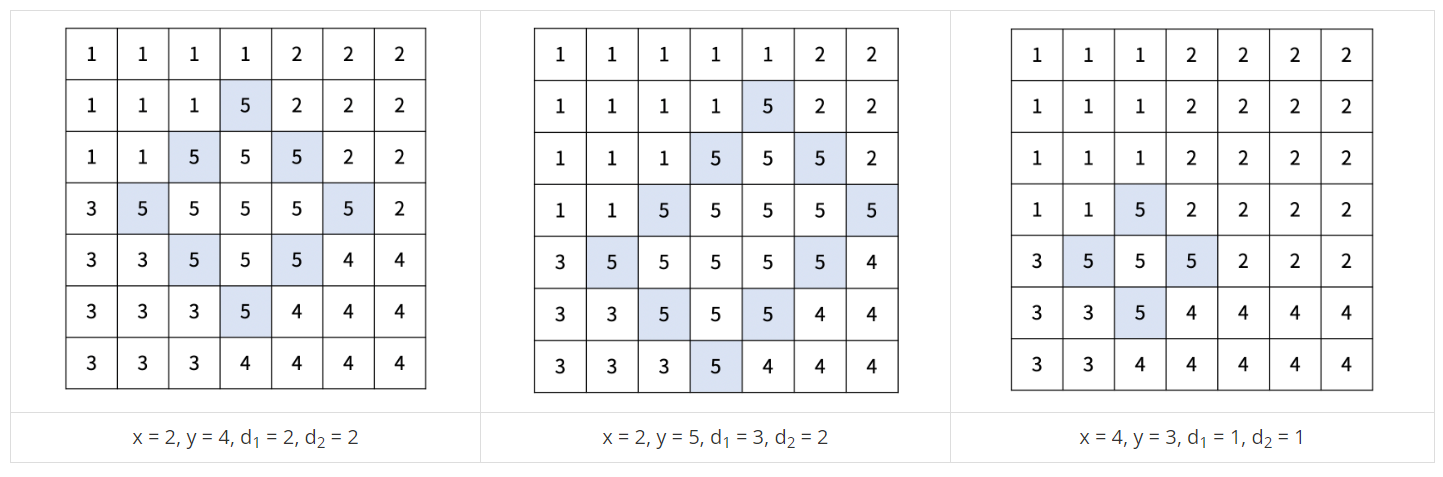
2차원의 지도에서 총 5개의 구역으로 나누고, 그 때의 가장 많은 인구가 들어간 구역과 가장 적은 인구가 들어간 구역의 차의 최솟값을 구하는 것이 문제의 요점이다.
5개의 구역으로 나누는 방법은 아래와 같다.
기준점 (x, y)와 경계의 길이 d1, d2를 정한다. (d1, d2 ≥ 1, 1 ≤ x < x+d1+d2 ≤ N, 1 ≤ y-d1 < y < y+d2 ≤ N)
다음 칸은 경계선이다.

• (x, y), (x+1, y-1), ..., (x+d1, y-d1)
• (x, y), (x+1, y+1), ..., (x+d2, y+d2)
• (x+d1, y-d1), (x+d1+1, y-d1+1), ... (x+d1+d2, y-d1+d2)
• (x+d2, y+d2), (x+d2+1, y+d2-1), ..., (x+d2+d1, y+d2-d1)

경계선과 경계선의 안에 포함되어있는 곳은 5번 선거구이다.
5번 선거구에 포함되지 않은 구역 (r, c)의 선거구 번호는 다음 기준을 따른다.

• 1번 선거구: 1 ≤ r < x+d1, 1 ≤ c ≤ y
• 2번 선거구: 1 ≤ r ≤ x+d2, y < c ≤ N
• 3번 선거구: x+d1 ≤ r ≤ N, 1 ≤ c < y-d1+d2
• 4번 선거구: x+d2 < r ≤ N, y-d1+d2 ≤ c ≤ N
  

문제 접근

나는 문제를 보고 3가지로 나누었다!

• 경계선 완전탐색하기
• 인구가 가장 많은 선거구와 가장 적은 선거구의 인구 차이 값 구하기
• 그 값의 최솟값 저장하기

될 수 있는 경계선 x,y,d1,d2를 모두 탐색하고 그 떄의 인구 차이 값을 구하고 마지막으로 값의 최솟값을 저장하여 값을 출력한다고 보면 된다.

문제 풀이

경계선 완전탐색하기

이건 매우 간단했다.
아래 코드와 같이 모든 상황을 전부 돌리고 문제에서 주어진 x,y,d1,d2의 범위를 그대로 넣어주면 된다.
저 조건문 내의 x,y,d1,d2가 나올 수 있는 모든 경우이다.

for x in range(1, N+1):
    for y in range(1, N+1):
        for d1 in range(1, N+1):
            for d2 in range(1, N+1):
                if 1 <= x < x+d1+d2 <= N  and 1 <= y-d1 < y < y+d2 <= N:
                	min_count = min(min_count,mancount(x,y,d1,d2))

인구가 가장 많은 선거구와 가장 적은 선거구의 인구 차이 값 구하기

이제 구역을 나누어야 한다.
근데 5번 구역은 조금 특이하다. 우리가 범위로 구역을 나누고자 해도 좀처럼 쉽게 나뉘어지지 않는다.
따라서 5번 구역은 따로 지정해주어야 했다.

5번 구역임을 표시하는 fifth 2차원 배열에 경계선을 따라 1을 넣어준다.
이렇게 한 다음 행을 기준으로 (x,y)와 (x+d1+d2,y)는 경계선이 겹치는 곳이기 때문에 반복문에서 제외하고 flag를 통해 열고닫아주면서 내부를 채워준다.

이제 5번 구역 표시가 끝났기 때문에 문제에서 주어진 1,2,3,4번의 범위를 그대로 넣어주고, fifth가 아니라면 count에 각각의 구역에 인구를 더해준다.
그 뒤 count에서 가장 큰 값 - 가장 작은 값을 return 한다.

def mancount(x,y,d1,d2):
    count = [0,0,0,0,0]
    # 경계구역 설정
    fifth = [[0 for _ in range(N+1)] for i in range(N+1)]
    for i in range(d1+1):
        fifth[x+i][y-i] = 1 # 왼쪽, 위로 향하는 대각선
        fifth[x+d2+i][y+d2-i] = 1 # 오른쪽, 위로 향하는 대각선
    for j in range(d2+1):
        fifth[x+j][y+j] = 1 # 오른쪽, 아래로 향하는 대각선
        fifth[x+d1+j][y-d1+j] =1  #왼쪽, 아래로 향하는 대각선
    for i in range(x+1,x+d1+d2):
        flag = False
        for j in range(N+1):
            if fifth[i][j]==1:
                if flag==True:
                    flag=False
                else:
                    flag=True
            else: 
                if flag==True:
                    fifth[i][j] = 1
    for i in range(1,N+1):
        for j in range(1,N+1):
            if i < x+d1 and j <= y and fifth[i][j] != 1:
                count[0] += pan[i][j]
            elif i <= x+d2 and y < j and fifth[i][j] != 1:
                count[1] += pan[i][j]
            elif x+d1 <= i and j < y-d1+d2 and fifth[i][j] != 1:
                count[2] += pan[i][j]
            elif x+d2 < i and y-d1+d2 <= j and fifth[i][j] != 1:
                count[3] += pan[i][j]
            elif fifth[i][j]==1:
                count[4] += pan[i][j]
    return max(count) - min(count)

그 값의 최솟값 저장하기

return된 값과 min_count의 값을 비교하여 더 작은 값을 min_count에 저장한다.
이렇게 저장된 값은 완전탐색했다면 모든 경우에서 가장 작은 값이 된다.
따라서 이를 출력하는 것이 정답이다.

min_count = float('inf')
for x in range(1, N+1):
    for y in range(1, N+1):
        for d1 in range(1, N+1):
            for d2 in range(1, N+1):
                if 1 <= x < x+d1+d2 <= N  and 1 <= y-d1 < y < y+d2 <= N:
                    min_count = min(min_count,mancount(x,y,d1,d2))

print(min_count)

제출 코드

# 경계선 완전탐색하기
# 인구가 가장 많은 선거구와 가장 적은 선거구의 인구 차이 값 구하기
# 그 값의 최솟값 저장하기
import sys
N = int(sys.stdin.readline())
# pan = [list(map(int, sys.stdin.readline().split())) for _ in range(N)]
pan = [[]]
for _ in range(N):
    pan.append([0] + list(map(int, sys.stdin.readline().split())))

def mancount(x,y,d1,d2):
    count = [0,0,0,0,0]
    # 경계구역 설정
    fifth = [[0 for _ in range(N+1)] for i in range(N+1)]
    for i in range(d1+1):
        fifth[x+i][y-i] = 1 # 왼쪽, 위로 향하는 대각선
        fifth[x+d2+i][y+d2-i] = 1 # 오른쪽, 위로 향하는 대각선
    for j in range(d2+1):
        fifth[x+j][y+j] = 1 # 오른쪽, 아래로 향하는 대각선
        fifth[x+d1+j][y-d1+j] =1  #왼쪽, 아래로 향하는 대각선
    for i in range(x+1,x+d1+d2):
        flag = False
        for j in range(N+1):
            if fifth[i][j]==1:
                if flag==True:
                    flag=False
                else:
                    flag=True
            else: 
                if flag==True:
                    fifth[i][j] = 1
    for i in range(1,N+1):
        for j in range(1,N+1):
            if i < x+d1 and j <= y and fifth[i][j] != 1:
                count[0] += pan[i][j]
            elif i <= x+d2 and y < j and fifth[i][j] != 1:
                count[1] += pan[i][j]
            elif x+d1 <= i and j < y-d1+d2 and fifth[i][j] != 1:
                count[2] += pan[i][j]
            elif x+d2 < i and y-d1+d2 <= j and fifth[i][j] != 1:
                count[3] += pan[i][j]
            elif fifth[i][j]==1:
                count[4] += pan[i][j]
    return max(count) - min(count)

# 경계선 x,y,d1,d2를 정해야 함

# 1번 선거구: 1 ≤ r < x+d1, 1 ≤ c ≤ y
# 2번 선거구: 1 ≤ r ≤ x+d2, y < c ≤ N
# 3번 선거구: x+d1 ≤ r ≤ N, 1 ≤ c < y-d1+d2
# 4번 선거구: x+d2 < r ≤ N, y-d1+d2 ≤ c ≤ N
# 5번 선거구: 그 외의 나머지 + 경계선
min_count = float('inf')
for x in range(1, N+1):
    for y in range(1, N+1):
        for d1 in range(1, N+1):
            for d2 in range(1, N+1):
                if 1 <= x < x+d1+d2 <= N  and 1 <= y-d1 < y < y+d2 <= N:
                    min_count = min(min_count,mancount(x,y,d1,d2))

print(min_count)